Abstract
The evolution of Earth’s climate on geological timescales is largely driven by variations in the magnitude of total solar irradiance (TSI) and changes in the greenhouse gas content of the atmosphere. Here we show that the slow ∼50 Wm−2 increase in TSI over the last ∼420 million years (an increase of ∼9 Wm−2 of radiative forcing) was almost completely negated by a long-term decline in atmospheric CO2. This was likely due to the silicate weathering-negative feedback and the expansion of land plants that together ensured Earth’s long-term habitability. Humanity’s fossil-fuel use, if unabated, risks taking us, by the middle of the twenty-first century, to values of CO2 not seen since the early Eocene (50 million years ago). If CO2 continues to rise further into the twenty-third century, then the associated large increase in radiative forcing, and how the Earth system would respond, would likely be without geological precedent in the last half a billion years.
Similar content being viewed by others
Introduction
The primary source of energy in the Earth’s climate system is incoming solar radiation, termed total solar irradiance, or TSI. At equilibrium, because of the requirement of energy conservation, the Earth’s radiative budget must balance such that TSI is equal to outgoing longwave radiation at the top of the atmosphere (a state known as radiative equilibrium). Since the radiation emitted by a body is a function of surface temperature, the Earth’s ‘effective temperature’ (TE) is the temperature at which radiative equilibrium is achieved assuming the Earth acts like a blackbody, and can be calculated (in K) using the following expression:

where Fs is the TSI (currently ∼1,368 Wm−2), σ is the Stefan–Boltzmann constant (5.67 × 10−8 W m−2K−4), A=0.29 (ref. 1) is the Earth’s average planetary albedo (the fraction of incoming radiation scattered or reflected back out of the atmosphere by clouds, particulates in the atmosphere and the Earth’s surface), and the factor of 4 accounts for the spherical and rotating nature of the Earth. The 31 K difference between TE and the observed surface temperature of the Earth (+14.0 °C or 287.1 K is the 1961–1990 mean2) is almost entirely due to the action of the greenhouse effect (for example, ref. 3).
The majority (∼75%) of the greenhouse effect is due to the warming effects of water vapour and clouds, with the non-condensing greenhouse gasses (predominantly CO2 and CH4) accounting for the remaining 25% (ref. 3). However, at the temperatures and pressures typical of the Earth’s surface, water vapour and clouds act as feedbacks rather than drivers of the greenhouse effect, with CO2 and CH4, and the other non-condensing GHGs (for example, N2O) determining the overall strength of the greenhouse effect3. Given this understanding, and that summarized in equation (1), the climatic evolution of the Earth over geological time is largely a function of the concentration of the non-condensing greenhouse gases, planetary albedo (A) and the TSI (Fs; for example, ref. 4).
Owing to the way the Sun generates energy though the nuclear fusion of hydrogen into helium, over time its luminosity has increased5. This is a relatively well-understood process and the TSI at any time  can be approximated by the following function5:
can be approximated by the following function5:

where Fs is the present day TSI (1,368 Wm−2), t is the time of interest since the formation of the Earth (Myrs) and t0 is the age of the Earth (4,567 Myrs (ref. 6), although here following ref. 5 we use a t0=4,700 Myrs). As a result, there has been an increase in TSI of ∼400 Wm−2 since the formation of the Earth. The following equation relates this change in TSI relative to today to radiative forcing (ΔFsol) assuming a constant planetary albedo (A) through time:

The global mean surface temperature change (ΔT, in K) for a given change in radiative forcing (ΔF, in Wm−2) can be described by:

Where S is the sensitivity parameter7, in K W−1m2. Following ref. 4, and assuming an effective emissivity, ɛ, of the Earth of 0.6 (that is, 40% of longwave radiation is absorbed by greenhouse gases in the atmosphere), equation (1) can be used to define the following equation that describes S for today’s climate (where the surface temperature=287.1 K) in the absence of any climate feedbacks (for example, water vapour, sea-ice etc.), also known as the Planck response (hence the subscript ‘P’)8:

SP depends on the overall strength of the greenhouse effect and the surface temperature of the Earth, and so this value is not necessarily applicable throughout Earth’s history; nonetheless, this treatment provides a first-order constraint that the long-term secular increase in TSI of 400 Wm−2 would be associated with a secular warming of at least ∼20 K over the last 4.5 billion years, if albedo and emissivity remained constant. Since the combined effect of the greenhouse gas and other climate feedbacks (for example, water vapour, lapse rate, sea-ice etc.) is positive8, this is a minimum estimate of S and when all climate feedbacks are considered, Sa (where ‘a’ denotes actuo after ref. 7) is likely in the range of 0.8– 1.6 K W−1 m2 (for example, refs 7, 9, 10, 11).
The actual evolution of Earth’s temperature through geological time is a subject of considerable debate (for example, ref. 12), yet there is a longstanding view that, despite the increase in solar output, Earth’s surface temperature was, for much of geological time, warmer, not colder, than today (for example, refs 13, 14). This apparent inconsistency is known as the ‘Faint Young Sun’ paradox and to reconcile the observation of a relatively stable climate in the face of increasing solar output through time requires a parallel change in some other factors that influence Earth’s radiative budget. First and foremost among these factors is thought to be a concomitant reduction in the strength of the greenhouse effect, and in atmospheric CO2 concentration in particular (for example, refs 15, 16). The radiative forcing from changing CO2 can be estimated using the following formulation17:

where \(\Delta F_{{\rm CO}_2 } \) is the radiative forcing from CO2 change (in Wm−2), C represents the concentration of CO2 at the time of interest and C0 is the pre-industrial concentration of CO2=278 p.p.m. For the decrease in atmospheric CO2 to balance the increase in solar output over time, the following equation is required to be true (or at least approximately so):

In this formulation we are ignoring the other non-condensing greenhouse gases (for example, CH4, N2O). This is partly out of practical necessity since there are currently no proxies for these gases, but is justifiable to a first order because variations in CO2 accounted for ∼80% of the greenhouse gas forcing on glacial–interglacial timescales4 and CO2 was likely the dominant greenhouse gas for the past 500 Myrs (refs 18, 19, 20).
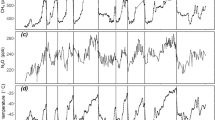
Testing whether the apparent stability of surface temperature is a consequence of the relative stability of climate forcing, therefore, requires high-density, high-quality data on past atmospheric CO2 levels. Consequently, in this study we compile the available CO2 data for the last 420 Myrs where, although the magnitude in the change of solar output is reduced relative to changes on longer timescales, data availability is sufficient to provide a detailed picture of the evolution of atmospheric CO2. The relative stability of climate over this interval is constrained by three lines of evidence: (i) the continued presence of complex life, given the thermal limits of metazoans (<40–50 °C; ref. 21) and despite a number of mass extinctions22; (ii) the continuous presence of liquid water and the occurrence of climate-sensitive sedimentary deposits (for example, coal versus glacial deposits) that indicate warm and cold periods but no evidence of an overall long-term secular trend (Fig. 1)23; and (iii) moderate tropical sea surface temperatures (25–40 °C) as recorded by oxygen and clumped isotope analysis of fossil marine carbonates24,25,26,27. Our new compilation shows that this climate stability was the result of a long-term decline in atmospheric CO2 that, in terms of radiative forcing, approximately cancelled out the increase in solar output. This long-term view of climate forcing provides a valuable geological context for potential levels of CO2 in our warming future.
Latitudinal extent of continental ice deposits23 (blue bars) and multi-proxy atmospheric CO2 (in p.p.m.) compiled from the literature (data found in Supplementary Data 1; symbols). CO2 from leaf stomata shown in blue circles, pedogenic carbonate δ13C as pink crosses, boron isotopes in foraminifera as green triangles, liverwort δ13C as dark blue filled circles and δ13C of alkenones as dark blue crosses. The most likely LOESS fit through the data, taking into account X- and Y- uncertainty is shown as the blue line (data found in Supplementary Data 2). 68 and 95% confidence intervals are shown as dark and light grey bands. Red line is a linear best fit (curved due to log-scale for y axis) and 95% confidence interval for least squares regression through the CO2 data (m=3.4±0.17 1 s.e.m., R2=0.26, P<0.0005). Black line is least squares fit through the LOESS best fit (blue line) resampled to original data density (m=3.5±0.12 1 s.e.m., R2=0.44, P<0.0005). Dashed line is pre-industrial CO2 (278 p.p.m.). Icehouse time intervals are indicated by a black band and greenhouse intervals by a white band.
Results
A new CO2 compilation
In order to better understand the role of the greenhouse effect in Earth’s climate evolution, we have compiled ∼1,500 discrete estimates of atmospheric CO2 from five independent techniques drawn from 112 published studies covering the last 420 Myrs (Supplementary Data 1). We uniformly apply a set of criteria and the latest understanding, described in the supplement, to screen the available CO2 records. By following these criteria, the ages and CO2 values associated with some records are revised (see Methods), and ∼1/5 of the published estimates have been excluded (leaving n=1,241 in our final compilation). This standardization process helps ensure the highest-quality compilation whose individual records can be more cleanly compared to one another.
Our new compilation is shown in Fig. 1 and, compared to older compilations, there is better agreement between the different methods of CO2 reconstruction28. In this case, this is largely due to the refinement of the pedogenic carbonate proxy following ref. 29 (see Methods). However, despite our efforts to improve the compilation, there are still relatively large uncertainties at times and disagreements remain between techniques for some time intervals (Fig. 1). It is also apparent that the early parts of the record rely on fewer observations and are characterized by a reduced diversity in proxy type (Supplementary Fig. 1). In order to gain a better appreciation of the multi-million-year evolution of CO2, and in light of these uncertainties and limitations we have followed a probabilistic approach where Monte Carlo resampling is used to generate 1,000 artificial time series of CO2 with each data point randomly perturbed within its age (X) and CO2 (Y) uncertainty. Each realization was then interpolated to a regular 0.5 Myr spacing and a LOESS fit was performed with the degree of smoothing optimized by generalized cross-validation30. At each time step the distribution of LOESS fits was evaluated and the maximum probability, hence the most likely value for long-term CO2, and the associated 68 and 95 percentile ranges were determined (Fig. 1 and Supplementary Data 2).
Our new compilation and probabilistic treatment reveals that for the last ∼420 Myrs, CO2, on the whole, has been elevated compared to pre-industrial values (278 p.p.m.). The highest CO2 values of ∼2,000 p.p.m. were reached during the Devonian (∼400 Myrs ago) and Triassic (220–200 Myrs ago), with individual estimates ranging up to a maximum of ∼3,700±1,600 p.p.m. at 215 Myrs. In contrast, values close to pre-industrial are found during much of the Carboniferous (∼300 Myrs ago) and late Cretaceous (∼80 Myrs ago). A linear fit to either the entire CO2 compilation, or a resampling of our LOESS fit to reflect the original data density, reveals that long-term average CO2 has declined over the last 420 Myrs by ∼3.4 p.p.m. per Myrs (Fig. 1).
Radiative forcing through the last 420 million years
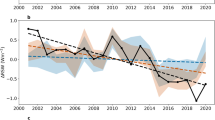
Radiative forcing from CO2 change can be calculated using equation (6). This can then be combined with the radiative forcing from the increase in solar output defined by equation (3) (Fig. 2a); the temporal evolution of the simple sum of these terms (ΔFCO2,sol) is shown in Fig. 2b. As has been noted elsewhere with prior Phanerozoic CO2 compilations (for example, refs 31, 32), there is a good first-order agreement between CO2 levels and the occurrence of greenhouse/icehouse states (Fig. 1): CO2 is high during greenhouse climate states and low during icehouse climates. Our data support previous work suggesting that, when ΔFCO2,sol is considered, icehouse states generally occur when climate forcing drops below approximately +1–2 Wm−2 (refs 31, 32). This treatment also reveals that for the last 420 Myrs, despite a gradual 4% increase in solar luminosity (equivalent to +9 Wm−2 of radiative forcing), there has been very little long-term change in ΔFCO2,sol (despite shorter-term fluctuations of up to 10 Wm−2), with a linear fit to all the data suggesting only a slight decrease of 0.004 Wm−2 per Myrs (±0.001 1 s.e.m.; P=0.0003; red line on Fig. 2b); a linear fit to our LOESS fit resampled with the original data density yields a slightly higher negative slope (−0.008±0.001 1 s.e.m.; P<0.0001; black line Fig. 2b). This indicates that the long-term decrease in CO2 over the last 420 Myrs has largely compensated for the increase in solar output over the interval. In terms of shorter-term radiative imbalances, 95% of the ΔFCO2,sol values are within ±7 Wm−2 and 68% within +5/−3 Wm−2 (Fig. 3). Thus, even on multi-million-year timescales (and sometimes shorter) the external radiative forcing (not considering the action of additional feedbacks internal to the climate system such as the ice-albedo feedback) has not varied beyond ±2.0% of the total incoming radiation (∼340 Wm−2).
(a) CO2 data (blue circles) and LOESS best fit (blue line; Supplementary Data 2) with ΔF for CO2 calculated as in equation (6). The change in solar forcing (ΔFsol) calculated using equations (2 and 3). (b) ΔFCO2,sol for data (blue circles) and LOESS best fit (blue line). Red line is a linear best fit and 95% confidence interval for least squares regression through the ΔFCO2,sol data (blue circles; m=−0.004±0.001 1 s.e.m., R2=0.01, P=0.0003). Black line is least squares fit through the LOESS best fit resampled to original data density (blue line; m=0.008±0.001 1 s.e.m., R2=0.06, P<0.0001). Icehouse time intervals are indicated by a black band and greenhouse intervals by a white band.
(a) Atmospheric CO2 with proxy data in blue (Supplementary Data 1) and LOESS best fit (Supplementary Data 2) in red. Vertical lines show maximum atmospheric CO2 from relevant representative concentration pathways (RCP) (colours)39 and from a 12,000 Pg C scenario (from ref. 41; Wink12K, black dashed line). (c) Proxy-based ΔFCO2,sol in blue and LOESS best fit in red along with relevant RCP scenarios (colours)39 and 12,000 Pg C scenario (black dashed line)41.
Discussion
The concentration of atmospheric CO2 on multi-million-year timescales depends largely on the balance between the input of CO2 from volcanism, metamorphism and organic carbon weathering and the output of CO2 from silicate weathering and organic carbon burial15. Since the magnitude of silicate weathering is climatically sensitive (that is, a function of temperature and precipitation; for example, ref. 33), silicate weathering also buffers the CO2 content of the atmosphere by acting as a negative feedback15. However, we note that in many modern settings silicate weathering is supply-limited33. Thus, for silicate weathering to operate as a climate feedback, the Earth must be sufficiently tectonically active to ensure an adequate supply of fresh minerals34.
The marked ‘double-hump’ pattern of the CO2 reconstruction (Fig. 1) that is also common to other compilations (for example, refs 28, 35) is likely caused by changes in the inputs and outputs of CO2 in response to the supercontinent cycle36. For example, the low CO2 during the Carboniferous (∼300 Myrs ago) and during the later parts of the Cenozoic (last 65 Myrs) was likely a result of a reduced volcanic flux and/or enhanced silicate weathering, at least in part due to higher continental relief during supercontinent construction phase. During the intervening greenhouse intervals the reverse was likely true (high volcanic flux and/or low silicate weathering due to low relief)36,37. An additional factor in the decline in CO2 was the overall enhancement of silicate weathering due to the expansion of the terrestrial biosphere over the last 400 million years or so (refs 16, 38). It is probably this expansion, along with the silicate weathering-negative feedback (facilitated by sufficiently active plate tectonic regime34), that was the key in keeping ΔFCO2,Sol relatively constant over the long term (for example, ref. 16). Indeed, as with previous compilations35, our new CO2 record largely agrees with the GEOCARB carbon cycle model that incorporates these long-term changes in silicate weathering (Supplementary Fig. 2), especially when the uncertainties in both records are considered35. This serves to further underscore the importance of the rise of the terrestrial biosphere, along with plate tectonics and silicate weathering, in ensuring climate stability through time16 and provides additional support for our broad understanding of the Earth’s long-term carbon cycle as encapsulated by the GEOCARB model35,38 (Supplementary Fig. 2).
Regardless of the ultimate cause for the observed relative stability in ΔFCO2,sol over the last 420 million years, business-as-usual emission scenarios (for example, representative concentration pathway RCP8.5)39 for fossil fuel emissions suggest that atmospheric CO2 could peak in 2,250 AD at ∼2,000 p.p.m. CO2 values as high as this were last seen in the Triassic around 220–200 Myrs ago (Figs 3 and 4). However, because of the steady increase in solar output over time, in terms of radiative forcing by the end of this century RCP8.5 is similar to the early Eocene, and by 2,250 AD exceeds what is recorded in the geological record for at least 99.9% of the last 420 Myrs (Figs 3 and 4). A recent study suggested that if both conventional and non-conventional fossil fuel reserves (amounting to ∼12,000 Pg C; ref. 40) were exhausted in such a business-as-usual scenario, atmospheric CO2 could rise to ∼5,000 p.p.m. by 2,400 AD (refs 41, 42), which is clearly higher, in terms of both forcing and absolute CO2, than at any time captured by our compilation (Figs 3 and 4, Wink12K scenario). Such a scenario therefore risks subjecting the Earth to a climate forcing that has no apparent geological precedent, for at least the last 420 Myrs. We should be aware of course of the limitations of the geological record, and it is debatable whether an extreme climate change event analogous to the Anthropocene, if it existed at all, would leave a detectable signal, given our current CO2 proxies and records43. Nonetheless, prolonged warm greenhouse climate states have occurred in the past, but the rates of climate change in the geological record are on the whole very likely slower than what we are currently experiencing (for example, ref. 44). Unabated fossil fuel use therefore has the potential to push the climate system into a state that has not been seen on Earth in at least the last 420 Myrs.
(a,b) Proxy-based atmospheric CO2 (Supplementary Data 1) on a log timescale with best fit LOESS and associated uncertainty envelope (Supplementary Data 2). (c) Ice core atmospheric CO2 from ref. 82 on log timescale. (d) Atmospheric CO2 on line timescale from ice core and observation record82 and future RCP8 and other41 scenarios (RCP3PD—grey, RCP4.5—orange, RCP6—red, RCP8.5—brown, Wink12k -black)38,40. (e–h) ΔFCO2,sol calculated from data shown in a–d as described in text. In (c) ΔFCO2,sol is calculated from ice core CO2 estimates assuming no change in solar output82. No change in solar output is also applied to the records in h.
Methods
Assembling the CO2 compilation
The new CO2 compilation here consists of 1,241 independent estimates coming from five proxy methods and 112 published studies. In putting this compilation together, we applied a uniform set of criteria described next to screen potential CO2 records. By following these criteria, the CO2 values associated with some records are revised, while other records are excluded all together. This standardization process helps ensure a high-quality compilation whose individual records can be more cleanly compared to one another. Of course, some of our criteria may be judged at some point to be incorrect. It is in this light, and in the spirit of full transparency, that we describe our criteria. We consider our compilation to be a ‘living document’, not only because in the future new records will be added but because existing records will be interpreted in new ways. The compilation can be found in Supplementary Data 1.
First, we excluded all goethite-based CO2 estimates45,46,47,48 due to uncertainties in modelling some of the isotopic fractionation factors49. We also excluded all B/Ca-based estimates50 because the environmental controls on B/Ca are currently not well understood51. The nahcolite proxy is based on well-described mineral phase equilibria52, but we exclude the published estimates because it is not possible to assign mean values (all values within a defined CO2 interval are equally probable). It is important to note, however, that the range described by these nahcolite estimates agree well with the other data in our compilation. We do not include the boron-based estimates of Pearson and Palmer53 owing to problems related to potential diagenesis, potential analytical issues, vital effects of extinct species and the evolution of seawater δ11B and alkalinity (as discussed in ref. 19). For the alkenone-based records of Pagani and colleagues54,55,56,57,58, we adopt the compilation of ref. 58 who imposed a uniform set of quality controls on the original data sets and used a TEX86 temperature record (versus the δ18O of ref. 54). We update all Cenozoic liverwort-based estimates59 with the atmospheric δ13C model of ref. 60.
For estimates calculated from stomatal ratios (SR, where SR=ratio of stomatal frequency in nearest living equivalent to fossil), two transfer functions to CO2 have been proposed: 1 SR=1 RCO2 and 1 SR=2 RCO2, where RCO2=ratio of atmospheric CO2 in the past to pre-industrial conditions (300 p.p.m.; refs 61, 62). Following Beerling and Royer63, we use these two functions to establish the uncertainty bounds in estimated CO2. Owing to the ad hoc nature of these functions, CO2 estimates from stomatal ratios should be considered semiquantitative only. We modify many of the stomatal-based estimates of Retallack64. First, we only use estimates associated with five or more cuticle fragments, as this is the minimum sampling required in most cases for robust estimates65. We use the quantitative transfer function of Royer65 for estimates coming from Ginkgo adiantoides, the fossil species considered conspecific with extant G. biloba66. For estimates coming from other species within the Ginkgo genus we use the stomatal ratio approach, and we exclude estimates not coming from Ginkgo as these other groups are too distantly related to Ginkgo and have not been calibrated correctly67.
A recent development that we have incorporated is the lowering of CO2 estimates from the pedogenic carbonate method29. This is because one of the key input parameters, the concentration of biologically derived CO2 in the soil (S(z)), had been overestimated in most paleosols by a factor of two or more29,68. Here we adjust most CO2 estimates assuming a S(z) of 2,000 p.p.m. (ref. 68). This is a simple correction that masks variability in S(z)69, but it is nonetheless a useful place to start and in most cases represents an improvement over previous estimates70. This is an area where we anticipate substantial revision in the near future. Along these lines, several proxies for S(z) have been proposed69,70,71,72,73,74,75,76, and we use estimates of S(z) derived from these methods when available. We also replace some of the pedogenic carbonate-based estimates of ref. 73 with those based on the same sediments74,75 because these newer studies provide better constraints on organic matter δ13C. Lastly, we collapse the high-resolution stomatal-based record of ref. 76 into one estimate calculated from the mean of the individual estimates.
Uncertainties in paleo-CO2 estimates have been assessed in different ways. Most earlier uncertainties associated with the pedogenic carbonate method, for example, only incorporate uncertainty in S(z); potential uncertainties in other input variables are ignored. In addition, errors associated with stomatal-based methods that involve quantitative regression equations usually only reflect uncertainty in the regressions; uncertainties in the fossil measurements are ignored. This means that error bars can convey different meanings, which hinders comparisons across methods. In recent years, Monte Carlo simulations for propagating uncertainty in multiple input variables have been developed for all five proxy systems11,55,59,77. So long as the reported percentile ranges are identical, these simulations facilitate better cross-method comparisons.
We attempt here to standardize reported uncertainties so that they incorporate uncertainty in all input variables; we also standardize the percentile levels (16 and 84; equivalent to ±1 s.d. for a normally distributed population). For uncertainties derived from Monte Carlo simulations that propagate uncertainties in most or all input variables (this covers most estimates from the alkenone, boron and liverwort proxies, as well as most recent estimates from pedogenic carbonates and stomata), we adjust if needed to the 16 and 84 percentile levels: for example, if the 2.5 and 97.5 percentiles are reported, we assume the population has a normal distribution and cut the uncertainties in half. Because most paleo-CO2 estimates have a right-skewed distribution, this means that we are overestimating the magnitude of the upper uncertainty and underestimating the magnitude of the lower uncertainty. For uncertainties with the pedogenic carbonate method derived by varying only S(z), we adopt for the 16 and 84 percentiles the generic recommendation of +100%/−50% of the median value calculated from multifactorial Monte Carlo simulations78; these uncertainties are larger and probably more representative than the reported uncertainties. Similarly, for stomatal estimates whose uncertainties only take into account variance in the transfer function, we assume 16 and 84 percentiles equal to +100%/−40% of the median value, a range that takes into account representative uncertainty in both the transfer function and the fossil measurements77.
All ages have been updated to the 2012 Geologic Time Scale79. Many CO2 estimates from terrestrial proxies have biostratigraphic (for example, ‘Maastrichtian’), magnetostratigraphic or chronostratigraphic constraints. For records with biostratigraphic or magnetostratigraphic constraints, we update their ages following the new Time Scale. Many CO2 estimates have no reported age uncertainties. In almost all cases, these estimates have excellent age control, the most common example being estimates from marine sediment cores (for example, all boron- and alkenone-based estimates). Some terrestrial-based data fall under this category too, for example, the Triassic–Jurassic sediments in the Newark Supergroup80. When no age uncertainty is reported we take the 1 s.d. to be 0.001 Myr for marine records and 4% for terrestrial records.
Monte Carlo sampling and LOESS fitting
Monte Carlo approach was used to generate 1,000 realizations of the multiproxy CO2 time series with each data point randomly perturbed within its age and CO2 uncertainty as given in Supplementary Data 1. For CO2 estimates with asymmetric uncertainties, we force symmetry by assuming ±1 s.d. is equal to the average offset between the median and the 16 and 84 percentiles. Each realization of the time series was then interpolated to a regular 0.5 Myr spacing and LOESS curves were fitted to each interpolated realization using the programme R81. The optimal degree of smoothing was determined for each interpolated realization using generalized cross-validation30. At each 0.5 Myr time step the distribution of LOESS curves was evaluated and the probability distribution was determined. From this probability distribution the most likely value (or probability maximum) and the upper and lower limits corresponding to 68 and 95% confidence limits were identified. These variables are given in Supplementary Data 2.
Owing to the nature of the proxies used the make-up and coverage of our new CO2 compilation varies considerably as a function of time. By grouping the data into 2.5 million year bins, Supplementary Fig. 1 shows that the number of observations in each 2.5 million year bin generally increases towards the present, with a notable exception of a peak at ∼200 million years ago at the Triassic–Jurassic boundary. Supplementary Fig. 1 also shows that the boron isotope and alkenone δ13C methods are restricted to the Cenozoic and liverwort δ13C proxy are concentrated in the middle part of the last 420 million years. Estimates based on fossil plant stomata appear focused in the last 200 million years, with only sporadic coverage over the early part of the interval. Only CO2 estimates from pedogenic carbonate δ13C method are relatively evenly spread across the last 420 million years. To examine the influence of this uneven distribution of proxy types we performed the LOESS fitting a further two times but without one of the dominant proxy systems (no-pedogenic carbonate, no-stomata), these alternatives are shown with the complete data set in Supplementary Fig. 3. While subtle variations exist, overall the large-scale structure remains intact, although if the pedogenic carbonate estimates are discarded the early part of the Phanerozoic is largely under sampled. In terms of long-term CO2 change, however, discarding all the estimates from either the pedogenic carbonate method or the stomatal method does not change our principal conclusions. For instance, the long-term CO2 decline over the last 420 million years without the pedogenic carbonates is 2 p.p.m. per million years, and without the estimates from the plant stomata method it is 4 p.p.m. per million years. Both of which are similar to the CO2 decline we determine for the complete data set (3.4 p.p.m. per million years), indicating that a long-term decline in CO2 over the last 420 million years is a robust observation. In terms of ΔFCO2,sol the long-term trends are also similar being 0.008±0.001 Wm−2 (R2=0.03 and P<0.001) and 0.0001±0.001 Wm−2 (R2=<0.001, P=0.94) for no-stomata and no-pedogenic carbonate, respectively.
Data availability
The authors declare that all data supporting the findings of this study are available within the Supplementary Information files associated with this manuscript.
Additional information
How to cite this article: Foster, G. L. et al. Future climate forcing potentially without precedent in the last 420 million years. Nat. Commun. 8, 14845 doi: 10.1038/ncomms14845 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Stephens, G. L. et al. The albedo of Earth. Rev. Geophys 53, 141–163 (2015).
Jones, P. D., New, M., Parker, D. E., Martin, S. & Rigor, I. G. Surface air temperature and its changes over the past 150 years. Rev Geophys 37, 173–199 (1999).
Lacis, A. A., Schmidt, G. A., Rind, D. & Ruedy, R. A. Atmospheric CO2: principal control knob governing Earth’s temperature. Science 330, 356–359 (2010).
Kohler, P. et al. What caused Earth’s temperature variations during the last 800,000 years? Data-based evidence on radiative forcing and constraints on climate sensitivity. Quart. Sci. Rev. 29, 129–145 (2010).
Gough, D. O. Solar interior structure and luminosity variations. Solar Phys. 74, 21–34 (1981).
Connelly, J. N. et al. The absolute chronology and thermal processing of solids in the solar protoplanetary disk. Science 338, 651–655 (2012).
Rohling, E. J. et al. Making sense of palaeoclimate sensitivity. Nature 491, 683–691 (2012).
Roe, G. Feedbacks timescales, and seeing red. Annu. Rev. Earth Planet. Sci. 37, 93–115 (2009).
Hansen, J. et al. Target atmospheric CO2: where should humanity aim? Open Atmos. Sci. J. 2, 217–231 (2008).
Royer, D. L., Berner, R. A. & Park, J. Climate sensitivity constrained by CO2 concentrations over the past 420 million years. Nature 446, 530–532 (2007).
Martínez-Botí, M. A. et al. Plio-Pleistocene climate sensitivity evaluated using high-resolution CO2 records. Nature 518, 49–54 (2015).
Grossman, E. L. in Reconstructing Earth’s Deep-time Climate: The State of the Art in 2012: Presented as a Paleontological Society Shor t Course at the Annual Meeting of the Geological Society of America, Charlotte, North Carolina, November 3, 2012, Vol. 18 (eds Ivany, L. C. & Huber, B. T.) 39–67 (The Paleontological Society, 2012).
Hren, M. T., Tice, M. M. & Chamberlain, C. P. Oxygen and hydrogen isotope evidence for a temperate climate 3.42 billion years ago. Nature 462, 205–208 (2009).
Blake, R. E., Chang, S. J. & Lepland, A. Phosphate oxygen isotope evidence for temperate and biologically active Archaean ocean. Nature 464, 1029–1032 (2010).
Walker, J. C. G., Hays, P. B. & Kastings, J. F. A negative feedback mechanism for the long-lasting stablization of the Earth’s surface temperature. J. Geophys. Res. 86, 9776–9782 (1981).
Schwartzman, D. W. & Volk, T. Biotic enhancement of weathering and the habitability of Earth. Nature 340, 457–459 (1989).
Byrne, B. & Goldblatt, C. Radiative forcing at high concentrations of well-mixed greenhouse gases. Geophys. Res. Lett. 41, 152–160 (2013).
Beerling, D. J., Fox, A., Stevenson, D. S. & Valdes, P. J. Enhanced chemistry-climate feedbacks in past greenhouse worlds. Proc. Natl Acad. Sci. USA 108, 9770–9775 (2011).
Anagnostou, E. et al. Changing atmospheric CO2 concentration was the primary driver of early Cenozoic climate. Nature 533, 380–384 (2016).
Bartdorff, O., Wallmann, K., Latif, M. & Semenov, V. Phanerozoic evolution of atmospheric methane. Global Biogeochem. Cycles 22, GB1008 (2008).
Nguyen, K. D. T. et al. Upper temperature limits of tropical marine ectotherms: global warming implications. PLoS ONE 6, e29340 (2011).
Raup, D. M. & Sepkoski, J. J. Jr Periodicity of extinctions in the geologic past. Proc. Natl Acad. Sci. USA 81, 801–805 (1984).
Crowley, T. J. in Tectonic Boundary Conditions for Climatic Reconstructions (eds Crowley, J. L. & Burke, K.) 3–17 (Oxford University Press, 1998).
Came, R. E. et al. Coupling of surface temperatures and atmospheric CO2 concentrations during the Palaeozoic era. Nature 449, 198–201 (2007).
Gothmann, A. M. et al. Fossil corals as an archive of secular variations in seawater chemistry since the Mesozoic. Geochim. Cosmochim. Acta 160, 188–208 (2015).
Cummins, R. C., Finnegan, S., Fike, D. A., Eiler, J. M. & Fischer, W. W. Carbonate clumped isotope constraints on Silurian ocean temperature and seawater δ18O. Geochim. Cosmochim. Acta 140, 241–258 (2014).
Veizer, J. & Prokoph, A. Temperatures and oxygen isotopic composition of the Phanerzoic oceans. Earth-Sci. Rev. 146, 92–104 (2015).
Royer, D. L. et al. CO2 as a primary driver of Phanerozoic climate. GSA Today 14, 4–10 (2004).
Breecker, D. O., Sharp, Z. D. & McFadden, L. D. Atmospheric CO2 concentrations during ancient greenhouse climates were similar to those predicted for A.D. 2100. Proc. Natl Acad. Sci. USA 107, 576–580 (2010).
Chandler, R. & Scott, M. Statistical Methods for Trend Detection and Analysis in the Environmental Sciences Wiley (2011).
Crowley, T. J. & Berner, R. A. CO2 and climate change. Science 292, 870–872 (2001).
Royer, D. L. CO2-forced climate thresholds during the Phanerozoic. Geochim. Cosmochim. Acta 70, 5665–5675 (2006).
West, A. J., Galy, A. & Bickle, M. Tectonic and climatic controls on silicate weathering. Earth Planet. Sci. Lett. 235, 211–228 (2005).
Foley, B. J. The role of plate tectonic-climate coupling and exposed land area in the development of habitable climates on rocky planets. Astrophys. J. 812, 1–23 (2015).
Royer, D. L. et al. Error analysis of CO2 and O2 estimates from the long-term geochemical model GEOCARBSULF. Am. J. Sci. 314, 1259–1283 (2014).
Berner, R. A. & Kothavala, Z. GEOCARB III: a revised model of atmospheric CO2 over Phanerozoic time. Am. J. Sci. 301, 182–204 (2001).
McKanzie, N. R. et al. Continental arc volcanism the prinicpal driver of icehouse-greenhouse variability. Science 352, 444–447 (2016).
Berner, R. A. The rise of plants and their effect on weathering and atmospheric CO2 . Science 276, 544–546 (1997).
Meinshausen, M. et al. The RCP greenhouse gas concentrations and their extensions from 1765 to 2300. Clim. Change 109, 213–241 (2011).
Rogner, H. H.- et al. in Global Energy Assessment—Toward a Sustainable Future. (eds Johansson, T. B. et al.) 423–512 (Cambridge University Press and the International Institute for Applied Systems Analysis, 2012).
Winklemann, R., Levermann, A., Ridgwell, A. & Caldeira, K. Combustion of available fossil fuel resources sufficient to eliminate the Antarctic Ice Sheet. Sci. Adv. e1500589 (2015).
Lenton, T. M. et al. Millennial timescale carbon cycle and climate change in an efficient Earth system model. Clim. Dyn. 26, 687–711 (2006).
Zalasiewicz, J., Williams, M., Haywood, A. & Ellis, M. The Anthropocene: a new epoch of geological time? Philos. Trans. R. Soc. A 369, 835–841 (2011).
Zeebe, R. M., Ridgwell, A. & Zachos, J. C. Anthropogenic carbon release rate unprecedented during the past 66 million years. Nat. Geosci. 9, 325–329 (2016).
Yapp, C. J. & Poths, H. Carbon isotopes in continental weathering environments and variations in ancient atmospheric CO2 pressure. Earth Planet. Sci. Lett. 137, 71–82 (1996).
Yapp, C. J. Fe(CO3)OH in goethite from a mid-latitude North American Oxisol: estimate of atmospheric CO2 concentration in the Early Eocene ‘climatic optimum’. Geochim. Cosmochim. Acta 68, 935–947 (2004).
Tabor, N. J. & Yapp, C. J. Coexisting goethite and gibbsite from a high-paleolatitude (55° N) Late Paleocene laterite: concentration and 13C/12C ratios of occluded CO2 and associated organic matter. Geochim. Cosmochim. Acta 69, 5495–5510 (2005).
Feng, W. & Yapp, C. J. Paleoenvironmental implications of concentration and 13C/12C ratios of Fe(CO3)OH in goethite from a mid-latitude Cenomanian laterite in southwestern Minnesota. Geochim. Cosmochim. Acta 73, 2559–2580 (2009).
Rustad, J. R. & Zarzycki, P. Calculation of site-specific carbon-isotope fractionation in pedogenic oxide minerals. Proc. Natl Acad. Sci. USA 105, 10297–10301 (2008).
Tripati, A. K., Roberts, C. D. & Eagle, R. A. Coupling of CO2 and ice sheet stability over major climate transitions of the last 20 million years. Science 326, 1394–1397 (2009).
Allen, K. A. & Hönisch, B. The planktic foraminiferal B/Ca proxy for seawater carbonate chemistry: a critical evaluation. Earth Planet. Sci. Lett. 345–348, 203–211 (2012).
Lowenstein, T. K. & Demicco, R. V. Elevated Eocene atmospheric CO2 and its subsequent decline. Science 313, 1928 (2006).
Pearson, P. N. & Palmer, M. R. Atmospheric carbon dioxide concentrations over the past 60 million years. Nature 406, 695–699 (2000).
Pagani, M., Arthur, M. A. & Freeman, K. H. Miocene evolution of atmospheric carbon dioxide. Paleoceanography 14, 273–292 (1999).
Pagani, M., Freeman, K. H. & Arthur, M. A. Late Miocene atmospheric CO2 concentrations and the expansion of C4 grasses. Science 285, 876–879 (1999).
Pagani, M., Zachos, J. C., Freeman, K. H., Tipple, B. & Bohaty, S. Marked decline in atmospheric carbon dioxide concentrations during the Paleogene. Science 309, 600–603 (2005).
Pagani, M. et al. The role of carbon dioxide during the onset of Antarctic glaciation. Science 334, 1261–1264 (2011).
Zhang, Y. G., Pagani, M., Liu, Z., Bohaty, S. M. & DeConto, R. A 40-million-year history of atmospheric CO2 . Philos. Trans. R. Soc. A 371, 20130096 (2013).
Fletcher, B. J., Brentnall, S. J., Anderson, C. W., Berner, R. A. & Beerling, D. J. Atmospheric carbon dioxide linked with Mesozoic and early Cenozoic climate change. Nat. Geosci. 1, 43–48 (2008).
Tipple, B. J., Meyers, S. R. & Pagani, M. Carbon isotope ratio of Cenozoic CO2: a comparative evaluation of available geochemical proxies. Paleoceanography 25, PA3202 (2010).
McElwain, J. C. & Chaloner, W. G. The fossil cuticle as a skeletal record of environmental change. Palaios 11, 376–388 (1996).
McElwain, J. C. Do fossil plants signal palaeoatmospheric CO2 concentration in the geological past? Philos. Trans. R. Soc. Lond. B 353, 83–96 (1998).
Beerling, D. J. & Royer, D. L. Fossil plants as indicators of the Phanerozoic global carbon cycle. Annu. Rev. Earth Planet. Sci. 30, 527–556 (2002).
Retallack, G. J. Greenhouse crises of the past 300 million years. Geol. Soc. Am. Bull. 121, 1441–1455 (2009).
Royer, D. L. in Causes and Consequences of Globally Warm Climates in the Early Paleogene (eds Wing, S. L., Gingerich, P. D., Schmitz, B. & Thomas E.) 79–93 (Geological Society of America Special Paper 369, 2003).
Tralau, H. Evolutionary trends in the genus Ginkgo. Lethaia 1, 63–101 (1968).
Vörding, B. & Kerp, H. Stomatal indices of Peltaspermum martinsii (Pteridospermopsida, Peltaspermaceae) from the Upper Permian Bletterbach Gorge and their possible applicability as CO2 proxies. Neues Jahrb. Geol. Paläontol. 248, 245–255 (2008).
Breecker, D. O., Sharp, Z. D. & McFadden, L. D. Seasonal bias in the formation and stable isotopic composition of pedogenic carbonate in modern soils from central New Mexico, USA. Geol. Soc. Am. Bull 121, 630–640 (2009).
Montañez, I. P. Modern soil system constraints on reconstructing deep-time atmospheric CO2 . Geochim. Cosmochim. Acta 101, 57–75 (2013).
Royer, D. L. Fossil soils constrain ancient climate sensitivity. Proc. Natl Acad. Sci. USA 107, 517–518 (2010).
Retallack, G. J. Refining a pedogenic-carbonate CO2 paleobarometer to quantify a middle Miocene greenhouse spike. Paleogeogr. Paleoclimatol. Paleoecol. 281, 57–65 (2009).
Cotton, J. M. & Sheldon, N. D. New constraints on using paleosols to reconstruct atmospheric pCO2 . Geol. Soc. Am. Bull 124, 1411–1423 (2012).
Ekart, D. D., Cerling, T. E., Montañez, I. P. & Tabor, N. J. A 400 million year carbon isotope record of pedogenic carbonate: implications for paleoatmospheric carbon dioxide. Am. J. Sci. 299, 805–827 (1999).
Tabor, N. J., Yapp, C. J. & Montañez, I. P. Goethite, calcite, and organic matter from Permian and Triassic soils: Carbon isotopes and CO2 concentrations. Geochim. Cosmochim. Acta 68, 1503–1517 (2004).
Montañez, I. P. et al. CO2-forced climate and vegetation instability during late Paleozoic deglaciation. Science 315, 87–91 (2007).
Doria, G. et al. Declining atmospheric CO2 during the late Middle Eocene climate transition. Am. J. Sci. 311, 63–75 (2011).
Beerling, D. J., Fox, A. & Anderson, C. W. Quantitative uncertainty analyses of ancient atmospheric CO2 estimates from fossil leaves. Am. J. Sci. 309, 775–787 (2009).
Breecker, D. O. Quantifying and understanding the uncertainty of atmospheric CO2 concentrations determined from calcic paleosols. Geochem. Geophys. Geosyst. 14, 3210–3220 (2013).
Gradstein F. M., Ogg J. G., Schmitz M. D., Ogg G. M. (eds). The Geologic Time Scale 2012 (Elsevier, 2012).
Schaller, M. F., Wright, J. D., Kent, D. V. & Olsen, P. E. Rapid emplacement of the Central Atlantic Magmatic Province as a net sink for CO2 . Earth Planet. Sci. Lett. 323–324, 27–39 (2012).
R Core Team. R: A language and environment for statistical computing. Available at http://www.R-project.org/ (2015).
Bereiter, B. et al. Revision of the EPICA Dome C CO2 record from 800 to 600 kyr before present. Geophys. Res. Lett. 42, 542–549 (2015).
Acknowledgements
We would like to dedicate this manuscript to the late Bob Berner for his seminal work in understanding the global carbon cycle. We are indebted to Gavin Schmidt and the readers and contributors of RealClimate.net for inspiring us to come up with this CO2 compilation and write this paper. We also thank the Royal Society for funding a Satellite Meeting at the Kavli Centre in 2011, ‘Reconstructing and understanding CO2 variability in the past’, at which the development of long-term compilations of CO2 was discussed. G.L.F. and D.J.L. acknowledge support from NERC (grant NE/I005595/1). Andy Ridgwell is thanked for supplying the CO2 emission scenarios from Winklemann et al.41 and for his thoughts on silicate weathering. The manuscript was greatly improved by the thorough reviews of an anonymous reviewer, Tim Lenton and Ethan Grossman.
Author information
Authors and Affiliations
Contributions
All authors conceived the idea for this manuscript, D.L.R. compiled the CO2 data set and G.L.F. performed the statistical analysis of the CO2 data. G.L.F. drafted the initial version of the manuscript and all authors contributed to the text.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures (PDF 495 kb)
Supplementary Data 1
Phanerozoic CO2 compilation used in analyses (XLSX 314 kb)
Supplementary Data 2
LOESS fit to the CO2 data set in Sup. Data 1. (XLSX 77 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Foster, G., Royer, D. & Lunt, D. Future climate forcing potentially without precedent in the last 420 million years. Nat Commun 8, 14845 (2017). https://doi.org/10.1038/ncomms14845
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms14845
This article is cited by
-
Global latitudinal gradients and the evolution of body size in dinosaurs and mammals
Nature Communications (2024)
-
Geographic range of plants drives long-term climate change
Nature Communications (2024)
-
Scale-Independent Variation Rates of Phanerozoic Environmental Variables and Implications for Earth’s Sustainability and Habitability
Mathematical Geosciences (2024)
-
Equisetum praealtum and E. hyemale have abundant Rubisco with a high catalytic turnover rate and low CO2 affinity
Journal of Plant Research (2024)
-
Multi-proxy evidence for sea level fall at the onset of the Eocene-Oligocene transition
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.