Abstract
The excitonic insulator is a long conjectured correlated electron phase of narrow-gap semiconductors and semimetals, driven by weakly screened electron–hole interactions. Having been proposed more than 50 years ago, conclusive experimental evidence for its existence remains elusive. Ta2NiSe5 is a narrow-gap semiconductor with a small one-electron bandgap EG of <50 meV. Below TC=326 K, a putative excitonic insulator is stabilized. Here we report an optical excitation gap Eop ∼0.16 eV below TC comparable to the estimated exciton binding energy EB. Specific heat measurements show the entropy associated with the transition being consistent with a primarily electronic origin. To further explore this physics, we map the TC–EG phase diagram tuning EG via chemical and physical pressure. The dome-like behaviour around EG∼0 combined with our transport, thermodynamic and optical results are fully consistent with an excitonic insulator phase in Ta2NiSe5.
Similar content being viewed by others
Introduction
Formation of exotic electronic phases driven by electron correlations is among the most intriguing phenomena in condensed matter physics. One such many-body ground state is the excitonic insulator being stabilized in materials where the conduction and valence band are either separated by a small energy gap (semiconductors) or are overlapping in energy by a small amount (semimetals). In narrow-gap semiconductors and semimetals, the Coulomb interaction between electrons and holes may lead to a spontaneous formation of electron–hole pairs, namely, excitons1,2,3,4. These charge neutral pairs can in analogy to superconductivity give rise to an unconventional insulating ground state—the excitonic insulator—which is characterized by a many-body gap 2ΔE opening in the single particle excitation spectrum (Fig. 1a). 2ΔE mirrors the exciton binding energy EB.
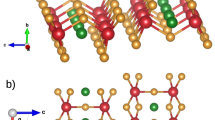
(a) Schematic phase diagram of excitonic gap formation as a function of EG. The dotted line indicates the crossover from semimetallic to semiconducting behaviour. The insets show the relation between EG and ΔE for the metallic and insulating limits. EG is the one-electron bandgap between conduction (red) and valence band (blue). The Coulomb interaction between electron- and hole-like excitations can lead to electron–hole pairing (exciton formation) and the opening of a new many-body excitation gap ΔE in the excitonic insulator phase. (b) The orthorhombic phase of Ta2NiSe5 shown in two orientations emphasizing the layered nature in the a–c plane, and (c) the TaSe6 and NiSe4 chains along the a direction (right).
The excitonic state is thermodynamically most stable for a zero-gap semiconductor EG=0. Reducing EG to a negative value (the semimetallic region) increases the electron/hole density in the one-electron band structure due to band overlap. The increased carrier density screens the effective Coulomb interaction between electrons and holes, and consequently suppresses the stability of excitonic pairs and therefore TC. This is in strong contrast to a simple hybridization gap, which also exists for a large band overlap. For positive EG (the semiconducting phase), the spontaneous formation of excitons is supressed with increasing EG and the excitonic phase becomes unstable against the semiconducting ground state for EG∼EB (refs 2, 4). In the semimetallic negative EG region where interactions are well screened and weak, the transition may be described by BCS mean-field theory due to the analogy with superconductivity2,4,5,6. On going to the positive EG region, one crosses over to a BEC-like limit as a consequence of strong coupling. This BCS–BEC crossover might be reflected in 2ΔE/kBTC being strongly enhanced over the BCS weak coupling value. In Fig. 1a, we schematically show the generally predicted phase diagram with its characteristic dependence of the excitonic transition temperature TC on the one electron bandgap EG (refs 2, 4).
Candidate materials previously discussed include TmSe0.45Te0.55 (refs 7, 8, 9) and 1T-TiSe2 (refs 10, 11). In both cases, transitions to possible excitonic insulator phases were observed. These transitions are however accompanied by strong finite q lattice distortions as expected in the excitonic scenario for such indirect-gap semiconductors. Analysis of the entropy changes involved based on specific heat showed that the transitions in these materials are driven not only by the small number of electrons and holes but are strongly influenced by lattice and spin degrees of freedom12,13. This is in contrast to the excitonic insulator limit, where lattice deformations play a secondary role1,2,3,4,5,6,14. Alternative scenarios such as a charge density wave or a band Jahn–Teller effect, which were put forward especially for 1T-TiSe2 (refs 15, 16), can therefore not be excluded to describe the relevant physics of these materials, leaving room for question on the existence of a canonical excitonic insulator phase.
Ta2NiSe5, first reported by Sunshine et al.17 and Di Salvo et al.18, is a layered compound stacked by van der Waals interactions and crystallizing in an orthorhombic Cmcm structure above TC, as illustrated in Fig. 1b,c (ref. 18). Each layer is composed of parallel chains of edge-shared TaSe6 octahedra and corner-shared NiSe4 tetrahedra, running along the crystallographic a axis.
Band structure calculations in the orthorhombic high-temperature phase of Ta2NiSe5 show that the conduction band minimum and the valence band maximum are almost degenerate at the Γ point14,19 implying a very small direct gap EG. The valence band is composed of Ni 3d orbitals with a Se 4p admixture while Ta 5d orbitals dominate the conduction bands. Note that the valence and the conduction bands in the orthorhombic phase belong to different irreducible representations of the crystal structure14,19. The formation of a single particle hybridization gap is therefore forbidden by crystal symmetry.
The small direct gap semiconductor realised in Ta2NiSe5 above TC is an ideal situation for the formation of an excitonic insulator phase. A semiconductor-to-insulator transition is indeed observed at TC≈326 K (ref. 18). This is accompanied by a very weak q=0 structural phase transition to monoclinic C2/c with the unit cell size remaining the same across the transition and whose small magnitude cannot account for the observed electronic changes14. This excludes a lattice distortion-mediated charge density wave mechanism driving the phase formation, as discussed in the case of Mo bronze20, suggesting it to be electronic in origin14. Recent X-ray photoemission spectroscopy (XPS) and angle-resolved photoemission spectroscopy (ARPES) measurements revealed a flattening of the valence band below TC, which was interpreted as the formation of an additional gap21. Based on these observations, the low-temperature phase was proposed to be an excitonic insulator. Ta2NiSe5 is distinct from other excitonic insulator candidates. First, due to the direct gap, the excitonic states do not require a finite q super-lattice modulation and can be accessed easily by optical spectroscopy. Second, electrons in Ta chains and holes in Ni chains are spatially separated in real space, which could stabilize the excitonic pair and hence the excitonic insulator.
Recognizing its uniqueness as a candidate excitonic insulator, electric transport, optical and specific heat measurements as well as physical and chemical pressure experiments were conducted on Ta2NiSe5 single crystals to test the validity of the excitonic insulator scenario. We will demonstrate that Ta2NiSe5 is a nearly zero-gap semiconductor at high temperatures with an optical gap Eop∼0.16 eV, comparable to the expected excitonic binding energy EB, developing below TC=326 K. The majority of entropy change at the transition appears to originate from thermally excited electrons and holes consistent with the thermodynamics of phase formation to be dominated by electronic degrees of freedom. The physical and chemical pressure experiments indicate the suppression of TC both by moving towards negative (semimetal) and positive (semiconductor) bandgap EG resulting in a dome-shaped TC versus EG curve around EG=0. All these results are consistent with those expected for a canonical excitonic insulator.
Results
Zero-gap semimetal-to-semiconductor transition
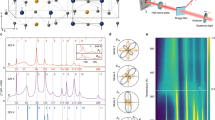
The transition in Ta2NiSe5 crystals is most readily seen in transport as shown in Fig. 2a. Here we present the resistivity ρa parallel to the Ta and Ni chains (I || a axis) as a function of temperature. A weak but well-defined kink is observed at TC=326 K. This agrees well with previous reports18. At high temperatures, the resistivity is essentially temperature independent over a wide range from 400 to 550 K. This means the transport gap is at most of the order of ∼0.05 eV, suggestive of an almost zero energy gap above TC. Right below TC, the resistivity increases rapidly, suggesting the opening of an additional gap. It is instructive for an excitonic insulator transition to present the data in form of an activation energy plot showing Eρ=−kBT2(‖lnρ/‖T) as a function of temperature (Fig. 2b; Supplementary Fig. 1). Eρ reflects an activation energy EA if the temperature dependence at a given temperature is approximated by a thermally activated behaviour ρ=ρ0exp(−EA/kBT) and therefore mirrors the energy scale of thermal excitation of charge carriers. Eρ shows a clear jump at TC consistent with theoretical calculations4,22, predicting a step-like increase of Eρ at TC. Eρ below the jump is 0.1−0.2 eV, which suggests a gap of the order of a few tenths of an eV opening below TC. At lower temperature below 100 K, we observe a suppressed activation energy Eρ. In this temperature regime, the conduction due to impurity states, with much lower energy scale of charge excitations, very likely dominates the temperature dependence.
(a) Temperature dependence of the in-plane resistivity of Ta2NiSe5 single crystal ρa (red) along the a axis parallel to the Ta and Ni chains, and ρc (blue) along the c axis perpendicular to the chains. An anomaly is observed at TC=326 K (emphasized by black triangle). The inset shows the temperature dependence of the resistivity ratio, ρc/ρa as an indicator of the in-plane anisotropy. (b) The temperature dependence of the activation energy Eρ of the resistivity data in a given by Eρ=−kBT2(‖lnρ/‖T). (c) Temperature dependence of heat capacity C of a Ta2NiSe5 single crystal. An anomaly in C at TC is clearly visible. The phonon contribution (black dashed line) is roughly estimated from a Debye fit to the low-temperature data below TC. The inset shows the excess specific heat ΔC/T around TC obtained from the raw heat capacity by subtracting the lattice contribution.
The resistivity perpendicular to the layer is orders of magnitude higher than the in-plane resistivity and we were not able to obtain a reliable estimate of the out-of-plane resistivity. Reflecting the presence of quasi-one-dimensional Ta and Ni chains, a moderate in-plane anisotropy is observed. As shown in Fig. 2a, above TC, the resistivity perpendicular to the chains (I || c axis), ρc, is larger than ρa along the chains by a factor of 6, indicating weak but appreciable electronic quasi-one-dimensionality. Below TC, this quasi-one-dimensionality in transport appears to be washed out, suggesting that the excitonic gap formation makes charge transport isotropic. This isotropy might be related to the flattening of the one-dimensional dispersion. We note that such temperature dependence in the ρc/ρa plot is absent in the family compound Ta2NiS5, which does not show any signature of an excitonic-like transition (Supplementary Fig. 2).
Gap formation below TC
An additional many-body excitation gap 2ΔE should open at TC due to the excitonic transition. While ARPES21 measurements are consistent with such a gap opening, a complete picture of the gap formation has not been unveiled yet due to the limitation of the measurement to occupied states below the Fermi level and the restricted temperatures at which the experiments were carried out. The formation of an excitation gap at TC is much more clearly evidenced by the optical conductivity spectrum with photon polarization along the chain direction a shown in Fig. 3. At high temperatures above TC, a broad continuum is observed with a hump-like structure around 0.3–0.4 eV, which is consistent with Ta2NiSe5 being an almost zero-gap semiconductor. On cooling below TC, the spectral weight is transferred from below an isosbestic point of E*∼0.3 eV to higher energies with a full gap of Eop∼0.16 eV forming. At 150 K, a gap structure with an absorption peak at 0.4 eV is well established. The opening of a gap is further demonstrated by the temperature evolution of the conductivity at an energy well below the gap which we show in the Supplementary Fig. 3. According to the previous ARPES study, the band maximum relative to the Fermi energy—the effective valence band gap—was estimated to be 0.17 eV, which is roughly consistent with the characteristic energy for spectral weight transfer (isosbetic point) E*∼0.3 eV and the optical gap Eop∼0.16 eV in the optical conductivity.
Optical conductivity spectra of Ta2NiSe5 single crystal at various temperatures, showing the opening of a charge excitation gap associated with the transition at TC=326 K. The gap of Eop≈0.16 eV is estimated from the usual extrapolation of the linear regime of conductivity (black dashed line). The electric polarization was parallel to the a axis.
Thermodynamic signature of phase transition
A clear anomaly in the specific heat C(T) can be identified at TC (Fig. 2c), with the shape being reminiscent of a BCS-type superconducting transition. This constitutes thermodynamic evidence for the opening of a gap in the electronic excitation spectrum at this transition. The entropy associated with the transition is roughly ΔS∼0.3 J mol−1 K−1. The density of states D at the quasi-one-dimensional band edge is of the order of 1 state per eV per unit formula14, yielding a rough estimate of density of electrons and holes at TC=326 K of D × kBTC∼0.03 per unit formula in the zero-gap case. This is not inconsistent with the Hall coefficient +RH∼10−2 cm3 C−1 (hole like) measured at TC (Supplementary Fig. 4), neglecting the ambiguity arising from the coexistence of electrons and holes. The quenched entropy of 3kB for 0.03 carriers corresponds to an entropy change ΔS∼0.03 × 3 R=0.7 J mol−1 K−1, agreeing with the experimental value within a factor of 2. This rough estimate implies that the majority of entropy change associated with the transition and therefore the thermodynamically relevant degrees of freedom originate from the electronic entropy indicating an electronically driven phase transition.
Phase diagram as a function of energy gap
The isovalent substitution of Se with Te and S was conducted to control the bandgap EG. Ta2NiS5 has compared with the isostructural Ta2NiSe5 a larger transport activation energy of Eρ∼0.2 eV in resistivity (inset, Fig. 5), indicative of the presence of a much larger bandgap EG than in Ta2NiSe5. As discussed, band calculations indicate that the valence band of Ta2NiSe5 is composed of Ni 3d and Se 4p orbitals14. With increased S-substitution, the hybridization between Ni 3d and Se 4p (S 3p) orbitals are weakened. This lowers the energy of the states at the top of the valence band while the conduction band is less affected, resulting in an overall enhancement of the bandgap EG compared to Ta2NiSe5. Changes in the Ta-chalcogen hybridization further enhance the band gap with increasing S-substitution but are predominantly affecting the energetically higher lying Ta-d bands above 1 eV (ref. 23). Tellurium doping, on the other hand, pushes the system in the opposite direction, likely bringing the nearly zero gap of Ta2NiSe5 to a negative region. Single crystals of the isovalent series Ta2Ni(Se1−xSx)5 and Ta2Ni(Se1−xTex)5 were grown. Te doping was limited up to x=0.2 due to the solubility limit likely due to the much larger ionic radius of Te.
(a) The activation energy plot Eρ=−kBT2(‖lnρ/‖T) for Ta2Ni(Se1−xSx)5 that clearly shows the systematic shift of TC with S doping. The inset shows resistivity curves (I || a axis) as a function of temperature. Triangles mark the transition temperatures for each sample. Variations in absolute values are due to uncertainties in, for example, exact sample dimensions. In b, we show the equivalent data for the Ta2Ni(Se1−xTex)5 series. (c) The activation energy plot as a function of temperature for a single high-pressure experiment showing both the systematic reduction of Eρ with pressure as well as the suppression of TC. Additional data from a high-temperature run are also included. The inset shows the equivalent resistivity data with emphasis of TC by triangles. (d) Equivalent data to c for Ta2Ni(Se0.8Te0.2)5.
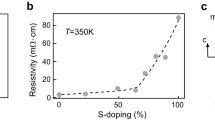
Phase diagram of the excitonic insulator phase in Ta2NiSe5 given by the transition temperature TC as a function of S doping (right) and pressure and Te doping (left), corresponding to the semiconducting and the semimetallic regions in the predicted phase diagram respectively. The pressure effect on Ta2Ni(Se0.8Te0.2)5 is also shown in the left region with an offset of chemical pressure of 0.5 GPa (see text). The shaded area in the left region indicates the region for phase separation behaviour at high pressures (see text), likely originating from a first-order transition. The inset shows the S doping x dependence of the transport activation energy of resistivity at high temperatures (500–550 K), E550 K. E550 K gives a measure of the one electron gap EG and indicates that EG increases monotonically as a function of x from almost zero for x=0 to at least a few tenths of an eV for x=1.0. The sulfur substitution level x and pressure P may therefore be mapped onto the single band gap EG in the high-temperature phase.
We show the activation energy plot of resistivity for Ta2Ni(Se1−xSx)5 and Ta2Ni(Se1−xTex)5 in Fig. 4a,b, respectively. It is clear that both by increasing and by decreasing the band gap TC is suppressed, meaning TC is peaked for Ta2NiSe5 with a nearly zero bandgap. The inset of Fig. 5 shows the evolution of the activation energy E550K for Ta2Ni(Se1−xSx)5 estimated from high-temperature data in the temperature range of 500–550 K well above TC (Supplementary Fig. 1), which should be closely related to the bandgap EG. It is monotonically increasing and can be described by a linear correlation to leading order as shown, implying the continuous and almost linear increase of the bandgap EG upon S-substitution. As E550K is systematically enhanced with increasing S-substitution, TC is suppressed to lower temperatures and eventually, for x>0.55, no phase transition was observed in the temperature dependent resistivity down to 2 K. For Ta2Ni(Se1−xTex)5, the decrease of resistivity at 350 K by ∼70% for x=0.1 and 0.2, respectively, indicates the continuous suppression of the energy gap (Fig. 4b). Although the range of substitution is limited, the plot of Eρ indicates a small but well resolved decrease of TC.
To confirm the suppression of TC by decreasing EG towards the negative side, namely by Te-substitution, physical pressure was applied to Ta2NiSe5. As can be seen from the activation energy plot in Fig. 4c, a clear decrease of TC is observed with increasing pressure. At 2.5 GPa, TC is decreased from 326 to 280 K, corresponding to a TC suppression rate of ∼20 K GPa−1, which can be reasonably ascribed to the decrease of the energy gap in the negative gap region. With 20% of Te-substitution, TC is reduced by 10 K, which is equivalent to 0.5 GPa of pressure. We performed the same pressure experiment also on 20% substituted Ta2Ni(Se0.8Te0.2)5 and observed again the suppression of TC with a rate of ∼20 K per GPa (Fig. 4d). Therefore, once we offset an effective chemical pressure equivalent to 0.5 GPa, the two TC (P) curves for pure and 20% Te substitute crystals fall onto a universal curve, strongly suggesting that the phase transition is controlled by a single parameter EG. In the pressure range above 2.4 GPa, we observe that upon increasing pressure further the transition temperature does not shift significantly, while the magnitude of the anomaly is substantially supressed (Fig. 4c,d) and conductivity in the low-temperature limit is significantly enhanced, suggestive of a first-order phase transition and the resultant phase coexistence. A recent pressure study up to 10 GPa on Ta2NiSe5 indeed indicates that there is a first-order structural phase transition at PC∼2.5 GPa, and the system becomes metallic above PC24. A reduction of resistivity under pressure is also measured for Ta2NiS5 but no phase transition was observed up to 3 GPa.
The control of TC by changing EG via chemical substitution and physical pressure effects can be summarized in the phase diagram shown in Fig. 5, where the pressure is a measure of decreasing EG on the negative EG side and the S-substitution is the measure of increasing EG on the positive side. Te-substitution was converted to equivalent pressure on the pressure axis. We clearly see the expected dome-shaped dependence of TC around EG∼0 (Ta2NiSe5).
Discussion
The high-temperature phase of Ta2NiSe5 appears to be very close to a zero-gap semiconductor making it an ideal candidate system for the stabilization of an excitonic insulator phase. Our optical data indeed show that below the phase transition temperature of TC=326 K, a gap Eop∼0.16 eV develops in the excitation spectrum consistent with the enhanced activation energy observed in our transport data. Significant spectral weight shifts occur from below the isosbestic point of ∼0.3 eV to higher energy scales of up to ∼0.6 eV. These energy scales should reflect the characteristic energy scales of the excitonic insulator and in particular experimentally constrains the scale of the exciton binding energy EB to be of the order of a few tenths of an eV. Expressed in terms of an effective temperature (0.1 eV corresponding to ≈1,000 K) EB is significantly larger than the experimental transition temperature to the excitonic insulator phase at 326 K, enabling the formation of this phase in Ta2NiSe5.
The exciton binding energy EB of the order of a few tenths of an eV is orders of magnitude larger as compared with those of conventional three-dimensional semiconductors. However, we argue that the unusual properties of Ta2NiSe5 explain at least in part the enhanced EB. The excitonic binding energies can be captured by EB=−13.6 eVμ/m0ɛ2. In this Rydberg formula, μ is a material specific effective mass and ɛ an effective permittivity25. First of all the d-band character of conduction (Ta 5d) and valence bands (Ni 3d) result in an effective reduced mass μ of the order of m0 as can be determined from ARPES data21 and band structure calculations14. This reduced mass is up to two orders of magnitude larger than in conventional direct gap semiconductors26. Furthermore the effective low dimensionality of the band structure and resulting physical properties are known to generally lead to a strong increase of the exciton binding energy26. Taken together, these effects can be expected to lead to a large enhancement of the exciton binding energy to a value consistent with tenths of an eV.
We now turn to the evolution of these properties under pressure and chemical substitution. The emerging phase diagram based on our transport measurements of TC as a function of the bandgap EG in the high-temperature phase shown in Fig. 5 is consistent with the theoretical expectation for the TC–EG dependence4, further supporting the excitonic state. TC is optimized for the nearly zero-gap semiconductor (EG∼0) Ta2NiSe5. On increasing EG in the solid solution Ta2Ni(Se1−xSx)5, the excitonic state should be suppressed and switch into a normal semiconductor when EG∼EB. For Ta2NiS5 located outside the dome in the phase diagram, the high-temperature (500–550 K) transport activation energy of ∼0.2 eV, shown in the inset in Fig. 5, implies an energy gap EG of ∼0.4 eV. Recent optical measurements show a similar trend with a gap of ∼0.25 eV at 350 K measured in Ta2NiS5 (ref. 23) compared with the effective zero gap in Ta2NiSe5 (Fig. 3). These results imply that, in contrast to Ta2NiSe5, EG in Ta2NiS5 is larger than EB, which has a weaker dependence upon sulfur substitution23. These findings are fully consistent with the absence of an excitonic transition in Ta2NiS5. In between these limits around x=0.5, the energy scale of the bandgap EG in the high-temperature phase can therefore be expected to become comparable with the exciton binding energy EB when crossing over from several hundreds of meV in Ta2NiS5 to effectively zero in Ta2NiSe5. This accounts for the stabilization of the excitonic insulator phase around that doping level.
We now turn our attention to the left hand part of the phase diagram. With going to the negative EG side with pressure, TC goes down with decreasing EG. This is consistent with the suppression of the excitonic binding due to the increased screening. The system is approaching the weak coupling BCS regime within the excitonic insulator scenario. Consequently the near-zero-gap Ta2NiSe5 with the highest TC is in the BCS–BEC crossover regime and a relatively strong coupling is anticipated. Indeed, the experimentally obtained Eop/kBTC∼6.5, a measure of coupling strength, for Ta2NiSe5 is much larger than 3.52 for weak coupling BCS, pointing to a moderately strong coupling.
Finally, we are not aware of any other electronically driven mechanism that could give rise to the observed behaviour. Since there is no evidence for magnetic-order scenarios such as Slater- or Mott-insulating phases can be readily excluded. Neither is there any Fermi surface nesting possible that could give rise to a partial gapping of the band structure. Indeed, the excitonic insulator scenario is the only theoretical proposal we are aware of that is consistent with all the observed experimental facts. In particular, the theoretically conjectured dome-shaped phase diagram we observe in this system is the cleanest among all excitonic insulator candidates and therefore represents a key advance in the search for this phase.
In summary, due to the relatively large effective mass of electrons and holes, and the reduced effective dimensionality, the layered direct gap semimetal Ta2NiSe5 can have a large exciton binding energy of a few tenths of an eV. The separation of electrons and holes confined within the quasi-one-dimensional chains may further help stabilizing the formation of excitons. The optical, transport and specific heat measurements on Ta2NiSe5 single crystals indicate that the system has an almost zero energy gap at high temperature but, below an electronically driven transition at TC=326 K, an excitation gap of Eop∼0.16 eV develops. The excitation gap is comparable to the expected exciton binding energy and is reasonably ascribed to the excitonic gap. The electronic phase diagram, TC as a function of the energy gap shows a dome-shaped behaviour centred at EG=0 expected for an excitonic insulator. Furthermore, the excitonic phase indeed disappears on increasing the energy gap EG when EG becomes comparable to the exciton binding energy, as expected. Based on this analysis, we conclude that an excitonic state is realized below TC=326 K in the nearly zero-gap semiconductor Ta2NiSe5.
Methods
Sample preparation
Single crystals of Ta2NiCh5 (Ch=S, Se and Te) were synthesized by chemical vapour transport. Elemental powders of tantalum, nickel and chalcogens (S, Se and Te) were mixed with a stoichiometric ratio and sealed into an evacuated quartz tube (∼1 × 10−3 Pa) with a small amount of I2 as transport agent. The mixture was sintered under a temperature gradient of 950/850 °C. After sintering for 1 week, needle-like single crystals were grown at the cold end of the tube.
Physical properties measurements
Electric resistivity and heat capacity measurements were carried out by using a PPMS (Quantum Design). Pressure experiments were carried out using a HPC-33 pressure cell by ElectroLab. High-temperature electronic resistivity was measured by using a bespoke measurement device. Optical parameter were determined using spectroscopic ellipsometry23.
Data availability
All relevant data are available from the corresponding authors upon request.
Additional information
How to cite this article: Lu, Y. F. et al. Zero-gap semiconductor to excitonic insulator transition in Ta2NiSe5. Nat. Commun. 8, 14408 doi: 10.1038/ncomms14408 (2017).
Publisher’s note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
Mott, N. F. The transition to the metallic state. Phil. Mag. 6, 287–309 (1961).
Halperin, B. I. & Rice, T. M. Possible anomalies at a semimetal-semiconductor transistion. Rev. Mod. Phys. 40, 755–766 (1968).
Kohn, W. Excitonic phases. Phys. Rev. Lett. 19, 439–442 (1967).
Jérome, D., Rice, T. M. & Kohn, W. Excitonic insulator. Phys. Rev. 158, 462–475 (1967).
Bronold, F. X. & Fehske, H. Possibility of an excitonic insulator at the semiconductor-semimetal transition. Phys. Rev. B 74, 165107 (2006).
Seki, K. et al. Excitonic Bose-Einstein condensation in Ta2NiSe5 above room temperature. Phys. Rev. B 90, 155116 (2014).
Bucher, B., Steiner, P. & Wachter, P. Excitonic insulator phase in TmSe0.45Te0.55 . Phys. Rev. Lett. 67, 2717–2720 (1991).
Wachter, B. Exciton condensation in an intermediate valence compound: TmSe0.45Te0.55 . Solid State Commun. 118, 645–650 (2001).
Wachter, P. The discovery of excitonium. J. Alloys Compd. 225, 133–138 (1995).
Wilson, J. A. Concerning the semimetallic characters of TiS2 and TiSe2 . Solid State Commun. 22, 551–553 (1977).
Cercellier, H. et al. Evidence for an excitonic insulator phase in 1T-TiSe2 . Phys. Rev. Lett. 99, 146403 (2007).
Bucher, B., Park, T., Thompson, J. D. & Wachter, P. Thermodynamical signatures of an excitonic insulator. Preprint at https://arxiv.org/abs/0802.3354 (2008).
Craven, R. A., Di Salvo, F. J. & Hsu, F. S. L. Mechanisms for the 200 K transition in TiSe2: a measurement of the specific heat. Solid State Commun. 25, 39–42 (1978).
Kaneko, T., Toriyama, T., Konishi, T. & Ohta, Y. Orthorhombic-to-monoclinic phase transition of Ta2NiSe5 induced by the Bose-Einstein condensation of excitons. Phys. Rev. B 87, 035121 (2013).
Hughes, H. P. Structural distortion in TiSe2 and related materials-a possible Jahn-Teller effect? J. Phys. C: Solid State Phys. 10, L319–L323 (1977).
Ishioka, J. et al. Chiral charge-density waves. Phys. Rev. Lett. 105, 176401 (2010).
Sunshine, S. A. & Ibers, J. A. Structure and physical properties of the new layered ternary chalcogenides tantalum nickel sulfide (Ta2NiS5) and tantalum nickel selenide (Ta2NiSe5). Inorg. Chem. 24, 3611–3614 (1985).
Di Salvo, F. J. et al. Physical and structural properties of the new layered compounds Ta2NiS5 and Ta2NiSe5 . J. Less Common Metals 116, 51–61 (1986).
Kaneko, T., Toriyama, T., Konishi, T. & Ohta, Y. Electronic structure of Ta2NiSe5 as a candidate for excitonic insulators. J. Phys.;Conf. Ser. 400, 032035 (2012).
Greenblatt, M. Molybdenum oxide bronzes with quasi-low-dimensional properties. Chem. Rev. 88, 31–53 (1988).
Wakisaka, Y. et al. Excitonic insulator state in Ta2NiSe5 probed by photoemission spectroscopy. Phys. Rev. Lett. 103, 026402 (2009).
Zittartz, J. Transport properties of the ‘excitonic insulator’: Electrical Conductivity. Phys. Rev. 165, 605–611 (1968).
Larkin, T. I. Excitonic Fano resonances in Ta2NiSe5 and Ta2NiS5. Online Publikationen der Universität Stuttgart. Available at http://dx.doi.org/10.18419/opus-8843 (2016).
Matsubayashi, K. Pressure-induced semiconductor-metal transition and superconductivity in Ta2NiSe5 . CiNii Articles Available at http://ci.nii.ac.jp/naid/110009990261/en (2015).
Knox, R. S. Theory of excitons. Solid State Phys. Suppl 5, 100 (1963).
Klingshirn, C. F. Semiconductor Optics Springer (2005).
Acknowledgements
We are grateful for Y. Ohta, T. Kaneko, Y. Katsura and T. Mizokawa for useful discussion. This work was partially supported by Grant-in-Aid for Scientific Research (S; grant no. 24224010) and by Grant-in-Aid for Scientific Research on Innovative Areas (grant no. JP15H05852). H.T. acknowledges support from the Alexander von Humboldt foundation.
Author information
Authors and Affiliations
Contributions
Y.F.L. and T.T. performed synthesis and measurement of physical properties under ambient pressure. H.K., A.W.R. and H.T. collected and analysed the data of transport properties. T.I.L. and A.V.B. measured and analysed the optical conductivity of single crystals. H.T. and B.K. designed and supervised the project. Y.F.L., A.W.R. and H.T. wrote the manuscript with inputs from all authors. All authors discussed and reviewed the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-5 (PDF 494 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Lu, Y., Kono, H., Larkin, T. et al. Zero-gap semiconductor to excitonic insulator transition in Ta2NiSe5. Nat Commun 8, 14408 (2017). https://doi.org/10.1038/ncomms14408
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms14408
This article is cited by
-
Terahertz parametric amplification as a reporter of exciton condensate dynamics
Nature Materials (2024)
-
Photogating-assisted tunneling boosts the responsivity and speed of heterogeneous WSe2/Ta2NiSe5 photodetectors
Nature Communications (2024)
-
Optical and electrical anisotropy regulation engineering of low-dimensional materials toward polarized detection and imaging applications
Rare Metals (2024)
-
Spectral signatures of a unique charge density wave in Ta2NiSe7
Nature Communications (2023)
-
Signature of spin-triplet exciton condensations in LaCoO3 at ultrahigh magnetic fields up to 600 T
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.