Introduction

Different mechanisms can extract energy from geostrophic flows and transfer it to unbalanced motions, from where it may be cascaded to smallest scale where irreversible molecular mixing takes place1,2. One pathway has been identified in the oceanic surface layer where frontogenesis in the intense fronts3 and filaments4 is an efficient way to transfer energy from the mesoscale to unbalanced motions. Different type of ageostrophic instabilities can provide a direct route from balanced mesoscale dynamics to unbalanced submesoscale behaviours5. In particular, atmospheric forcing at fronts can make the flow unstable to symmetric instability and initiate a forward cascade of energy down to dissipation6,7,8. The near-inertial wave field excited by the wind may also extract significant energy from the geostrophic flows9,10. Another pathway lies at the bottom of the ocean where interactions of geostrophic flows with small-scale bottom topography generate internal gravity waves that can break and dissipate energy at small scales11. There is a more recent and much less studied mechanism associated with the generation of submesoscale flows by interaction of geostrophic flows with steep topographic slopes12,13,14.

Most of the mean kinetic energy (MKE) is concentrated in the intense western boundary currents, such as the Gulf Stream, and they are known to be sites of elevated eddy energy dissipation15. It is, thus, an ideal place to study the interaction of geostrophic flows with topography and investigate the possible impact of topography on energy dissipation and mixing.

To this end, we perform realistic simulations of the Gulf Stream using very high horizontal and vertical resolutions (Δx=200 m, see ‘Methods’ section) that allow us to adequately resolve submesoscale motions in the range 1–30 km. The results show that the interaction of the incident geostrophic flow with topography can generate unbalanced submesoscale turbulence that leads to elevated local dissipation and mixing outside the oceanic boundary layers. Energy dissipated locally through the process is comparable to the energy dissipated in intense surface frontogenetic regions. Interior regions of high energy dissipation, with the implication of strong vertical mixing of material properties across stably stratified isopycnal surfaces, is of great interest for its potential significance for the energy budget of the general circulation and the maintenance of the density stratification.

Results

Topographic vorticity generation

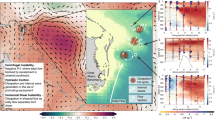
The Gulf Stream strongly interacts with topography as it flows through the Florida Straits. The Stream is constrained by the Florida Shelf on its cyclonic side and the Great Bahama Bank and the Little Bahama Bank on its anticyclonic side (Fig. 1a). On the cyclonic side, flow-topography interactions lead to barotropic shear instability and formation of streets of submesoscale vortices14. The topographic drag against the slope amplifies the cyclonic shear by generating large positive vertical vorticity values within the sloped turbulent bottom boundary layer. The flow partially separates from the topography downstream from the Straits, and due to the large horizontal velocity shear, often becomes unstable to submesoscale barotropic instability, rolls up and forms streets of submesoscale vortices. Submesoscale cyclones will also similarly be created at any place where a current interacts with the topography on its left (in the northern hemisphere), which corresponds to a current that flows in the direction opposite to the Kelvin wave propagation direction.

Figure 1: Topographic generation of negative vorticity along the Bahamas Banks.
figure 1

(a) Instantaneous surface relative vorticity ζ=vx−uy, normalized by f, for the Gulf Stream along the southeast US seaboard as simulated by ROMS. The boundaries of the successive nested domains (Δx=2.5, 0.75 and 0.20 km) are delineated by thick grey lines. (b) Zoomed-in view of the Gulf Stream along the Bahamas Banks. Green contours show region of high energy dissipation (depth-integrated energy dissipation >2 × 10−4 W m kg−1). Localized regions with negative vorticity and high energy dissipation rates are created by the currents flowing along the topographic slopes of the Bahamas Banks.

Full size image

On the anticyclonic side of the Stream there is a similar topographic vorticity generation, but with the opposite sign (Fig. 1a,b). The topographic drag against the slope amplifies the anticyclonic shear and generates large negative vertical vorticity values. Following the sequence of processes described in the context of the California Undercurrent12, relative vorticity can locally become much smaller than −f, where f is the Coriolis frequency, and Ertel’s potential vorticity (PV, see ‘Methods’ section) can become negative, which is a criterion for ageostrophic centrifugal instability16.

Negative values of PV can be spotted in different regions (Fig. 2) where the flow strongly interacts with the topography: (i) along the slope of the Great Bahama Bank, downstream of the Bimini Islands (26°N, 79.3°W); (ii) along the western part of the Little Bahama Bank; (iii) at the southern tip of the Grand Bahama Island (26.5°N, 78.8°W); and (iv) on the northern side of the Great Bahama Bank (26°N, 78.5°W). The last two locations correspond to the interaction of a cyclonic eddy trapped in the Northwest Providence Channel, which separates the Little Bahama Bank from the Great Bahama Bank (Fig. 1b). It is a recurrent and observed feature of the local circulation17. PV at all the aforementioned locations is dominated by its vertical component. The negative values are obtained through a combination of stable stratification and strong negative values of vertical vorticity. Negative values of PV also coincide with high energy dissipation (Fig. 1b).

Figure 2: Generation of negative potential vorticity and centrifugal instability.
figure 2

Snapshots of PV (in 10−8 s−3) and velocity (vectors) at (a) z=−50 m and (b) z=−100 m. Localized regions with highly negative PV are created by the currents flowing along the topographic slopes of the Bahamas Banks.

Full size image

The sequence of processes consists of three different steps: negative PV generation within the bottom boundary layer; separation of the negative PV strip from the slope; and intense small-scale instabilities and energy dissipation in the separated wake (Fig. 3). The negative PV sheet forms along the bottom slope where vertical and horizontal scales of the boundary sheared layer are locally about 50 and 500 m with a cross-shelf bottom slope as high as 0.1 along the Grand Bahamas Bank (Fig. 3a). Given a current of 0.5–1 m s−1, we can evaluate the scale of the vertical vorticity in the boundary layer as , which is consistent with the instantaneous maximum relative vorticity values in the simulation. The model has 100 levels in the vertical with grid stretching near the bottom such that the vertical resolution does not exceed 2 m in the boundary layer in the region of strong topographic vorticity generation.

Figure 3: Submesoscale centrifugal instability of the boundary layer.
figure 3

(a–d) Vertical sections of potential vorticity (PV, in 10−8 s−3) and (e–h) energy dissipation from upstream to downstream along the Great Bahamas Banks (see yellow lines in Fig. 2) showing (a,e) PV generation, (b,f) separation from the slope, and (c,d,g,h) centrifugal instability in the wake. Density is shown in black contours with an interval of 0.5 kg m−3 and along-slope velocity is shown in green contours with an interval of 0.2 m s−1.

Full size image

Centrifugal instability

A change in the sign of PV is a sufficient condition for instability in an unbounded fluid16. The instabilities that arise can extract their kinetic energy from the eddy potential energy (EPE) through the vertical buoyancy flux (VBF, see ‘Methods’ section) or from the MKE through a combination of the vertical shear production term (VRS) and the horizontal shear production term (HRS). Centrifugal (or inertial) instability is triggered when the relative vorticity is smaller than −f and extracts its energy mostly from the lateral shear (HRS>0)18. The positive conversions from mean to eddy kinetic energy (EKE) seen in the regions of sustained negative potential vorticity generation (Fig. 4b,d) are due to the lateral shear. The vertical shear production term is an order of magnitude smaller (Supplementary Fig. 1). The vertical buoyancy flux term (Fig. 4e) is negative in the region of instability. This is indicative of centrifugal instability, and it is consistent with the results obtained from comparisons of model and linear instability analysis for the California Undercurrent13.

Figure 4: Energy dissipation and mixing.
figure 4

Time mean depth-integrated terms of the EKE equation: (a,c) dissipative terms, (b,d) conversion from MKE to EKE, and (e) conversion from EPE to EKE. Bottom panels show a zoomed view in the region of strong generation along the Great Bahama Bank (black rectangle in a). The mean transport stream function is shown in green with a 5 Sv interval (1 Sv=106m−3s−1). Units for energy rates are W m kg−1. Topography is shown in black contours at 0, 100, 500 and 1,000 m isobaths.

Full size image

The horizontal shear production term has a two-signed pattern in regions of topographic interactions. The energy conversion is from eddy to mean kinetic energy on the upstream sides where the bottom drag over the slope intensifies the mean horizontal velocity shear and suppresses cross-stream velocity perturbations growth. The energy conversion is from mean to eddy kinetic energy downstream from the topographic features, indicative of instability and eddy generation.

Energy dissipation

Locations of sustained generation of centrifugal instability correspond to EKE dissipation maxima (Fig. 4a,c). Where the current directly interacts with the topography (that is, upstream from the Bimini Islands), there is dissipation of MKE due to the vertical mixing occurring in the bottom boundary layer that is directly triggered by the bottom drag (Supplementary Fig. 2). Downstream from the generation sites the dissipation is also dominated by the vertical mixing term, but in the ocean interior, outside of the surface and bottom boundary layers, where it represents the parameterization of small Richardson number processes and static instabilities19. The vertically integrated dissipation rates of EKE reach values up to 8 × 10−4 W m kg−1 instantaneously at 26°N following separation of the negative PV strip from the slope (Fig. 3b). It is of the same order as the dissipation rates observed in an intense surface front within the Kuroshio Current8 integrated over the mixed-layer.

The EKE dissipation rates averaged over a 3 months period (Fig. 4c) have values up to 2 × 10−4 W m kg−1, which are only slightly smaller than the instantaneous values. This shows how remarkably sustained are the topographic generation of vorticity and the subsequent centrifugal instability. The kinetic energy dissipation rates are roughly an order of magnitude larger than the dissipation rates due to the same mechanisms in the California Undercurrent12, where the velocity shears are weaker. The rate of conversion from mean to eddy kinetic energy downstream from the Bimini Islands reaches values up to 4 × 10−4 W m kg−1 (Fig. 4d) and are on average three times larger than the values of the EKE dissipation rates at the same location. The ratio between the EKE dissipation and the EKE source, averaged over the region of eddy generation downstream from the Bimini Islands only (Fig. 4d), is 35%, showing that about a third of the energy extracted from the mean flow by the instability processes and small-scale turbulence is locally dissipated. A smaller fraction of the EKE is converted to EPE through VBF (Fig. 4e). The ratio of the EKE converted to potential energy divided by the EKE lost to viscous dissipation gives the efficiency of the mixing20. Averaged over the domain of (Fig. 4e) in the region where VBF<0 and the dissipation is large (>0.5 × 10−4 W m kg−1), this efficiency is about 0.20.

The topographic generation of centrifugal instability is remarkably sustained in time given that the current is forced through the Straits and interacts with topography consistently throughout the year. There is a modulation in the frequency and intensity of events following the seasonal variations of the Gulf Stream transport. The Gulf Stream transport varies by a few Sverdrups between summer where it is maximum and winter where it is minimum21. Maxima in transport are directly correlated with maxima in the intensity of the velocity shear created in the bottom boundary layer and the amplitude of the energetic dissipation induced by the centrifugal instability.

Discussion

The mechanism is generic for boundary slope currents that flow in the direction of Kelvin wave propagation (with the topography on their right in the northern hemisphere) where the PV is reduced in the bottom boundary layer22. Under these conditions, strong vertical vorticity can be generated within the bottom boundary layer that subsequently separates over complex topography and triggers intense centrifugal instability. A cyclonic eddy encountering a topographic slope will trigger the same mechanism23. This could explain, for example, the elevated levels of turbulence observed on the sides of the Bermuda Island during an interaction with a cyclonic Gulf Stream ring24. This could also provide another mechanism, alongside the forcing of the negative wind stress curl, responsible for the formation of the submesoscale anticyclones with large negative vorticity values (−1.7f) observed in the lee of the Hawaiian Islands25. Flows moving in the direction opposite to the Kelvin wave propagation direction, on the other hand, will generate positive vertical vorticity and eventually trigger barotropic shear instability14. But, the presence of recurrent cyclonic eddies on the cyclonic side of a current along the slope, as a results of the baroclinic or barotropic instability of the mean current, will also induce local reversals of the current and trigger the sequence of processes described here leading to centrifugal instability23.

The sequence is much like the anticyclonic events in the California Undercurrent12, which gives birth to the submesoscale coherent vortices (SCVs26) known as Cuddies. In the case of the Gulf Stream, the vortices produced by the instability have limited lifetimes and upscaling because they remain in the vicinity of the high shear and strain of the Gulf Stream. However, this process is also a very likely candidate for the formation of SCVs all around the globe27, including the Meddies that are formed from the Mediterranean Undercurrent along the Iberian Peninsula28, the SCVs that are formed in the Peru-Chile Undercurrent29, the SCVs observed in the northwestern Mediterranean Sea30, the SCVs that spread the Persian Gulf Outflow waters in the Gulf of Oman31, or the Labrador Sea outflow eddies that are formed along the Grand Banks32.

The volume integrated EKE dissipation and rate of conversion from mean to eddy kinetic energy are both of order 0.4 GW (109 W) over the domain of Fig. 4a (Fig. 5). To evaluate the contribution of this mechanism to the global kinetic energy budget, it is interesting to scale up this value to the entire ocean and compare it to the 0.8 TW (1012 W) that the wind provides to the geostrophic circulation33. The area of the ocean that has a topographic slope larger than 1 degree represents 29% of the total area34. The Gulf Stream is a highly energetic region and currents are generally weaker than the currents considered here (0.5–1 m s−1), such that the dissipation rates are likely to be on average an order of magnitude smaller. Assuming finally that half of the currents are flowing in the direction of Kelvin wave propagation, we arrive at a global dissipation rate of 0.05 TW, that is, in the range of 0.01–0.1 TW, which represents a significant route toward dissipation. The variability due to mesoscale eddies impinging on topography at western boundaries, islands, ridges or seamounts, is difficult to estimate and would require a more quantitative analysis using global current data from observations or global model outputs to come to a more comprehensive estimate of the energy dissipated by centrifugal instability on the boundaries.

Figure 5: Eddy kinetic energy budget.
figure 5

Volume integral of the EKE balance equations terms (equation 1) over the domain plotted in Fig. 4a. Units for energy rates are GW (109 W). The main source of EKE is the conversion from mean to eddy kinetic energy due to centrifugal instability and the main sink is the vertical mixing .

Full size image

The enhanced energy dissipation and tracer mixing due to the submesoscale turbulence, and the tracer transport by submesoscale coherent vortices, are processes that need to be quantified for their effect on the general circulation. These processes are missed by global climate models and eddy-resolving global ocean circulation models, where the grid size is generally much larger than the scale of the boundary layer, and will need to be parameterized.

Methods

Numerical simulation

The high resolution realistic simulation of the Gulf Stream is performed with the Regional Oceanic Modeling System (ROMS35), which solves the free surface, hydrostatic and primitive equations. We use a nesting approach36 with successive horizontal grid nesting refinements from a parent grid resolution of Δx≈6 km, covering most of the Atlantic Ocean to successive nested grids with Δx=2.5 km, Δx=750 m, and Δx=200 m (see domains in Fig. 1). The highest resolution solution is 4 months long and has 1,300 × 2,300 points in the horizontal with a resolution of 200 m and 100 vertical topography-following vertical levels. Vertical mixing of tracers and momentum is computed using a K-profile parameterization19, which represents in the ocean interior small Richardson number processes and static instabilities. The effect of bottom friction is parameterized through a logarithmic law of the wall with a roughness length Z0=0.01 m. The use of a topography-following coordinate, with significant grid stretching near the bottom such that the boundary layer mixing profile is reasonably well resolved, is of great advantage in calculating flows over complex terrain. The simulation is forced at the surface by realistic daily winds and diurnally modulated surface fluxes. Characteristics of the mean structure and variability of the simulated Gulf Stream in the Florida Straits and along the U.S. seaboard have been validated with satellite and in situ observations14,37. While one can question the details of how the model reacts to centrifugal instability, it has been shown that overall characteristics are accurate13.

Potential vorticity

The Ertel PV is defined as q=ωa·∇b, the dot product of the absolute vorticity ωa=f z+∇ × u and the gradient of buoyancy . f is the Coriolis parameter, u is the velocity, ρ the in situ density, ρ0 the mean reference density and g the gravitational acceleration.

Eddy kinetic energy equation

The eddy kinetic energy is , where the overline denotes a time average over the last 3 months of the simulation, and the prime denotes fluctuations relative to the time average. The EKE equation is formed by subtracting the energy equation of the mean flow (Supplementary Methods) from that of the total flow38:

where Cartesian tensor notation with summation convention has been used, i=1, 2, j=1, 2, 3; ui are the horizontal components of the velocity vector uj; u3=w is the vertical velocity; p is the pressure anomaly; b=− is the buoyancy anomaly; and are the vertical mixing and horizontal diffusion terms in the horizontal momentum equations. The EKE dissipation in the model is the sum of the dissipative effects of the two latter terms. Units are m3 s−3=W m kg−1. The spatial structure of all terms from the mean and eddy kinetic energy balance equations are shown in Supplementary Figs 2 and 3. The volume integrated EKE budget for the domain of Fig. 4a,b is shown in Fig. 5. The volume integrated MKE budget over the same domain is shown in Supplementary Fig. 4.

Energy conversion

The conversion from mean to eddy kinetic energy (MKE→EKE) can be due to the horizontal shear production term or to the vertical shear production term (ref. 18). The conversion from eddy potential to eddy kinetic energy (EPE→EKE) corresponds to the vertical buoyancy flux , where w is the vertical velocity and b the buoyancy anomaly.

Code availability

The ocean model (ROMS) is available from http://www.romsagrif.org.

Data availability

The data that support the findings of this study are available from the corresponding author upon request.

Additional information

How to cite this article: Gula, J. et al. Topographic generation of submesoscale centrifugal instability and energy dissipation. Nat. Commun. 7:12811 doi: 10.1038/ncomms12811 (2016).