Abstract
Skyrmions are particle-like topological entities in a continuous field that have an important role in various condensed matter systems, including two-dimensional electron gases exhibiting the quantum Hall effect, chiral ferromagnets and Bose–Einstein condensates. Here we show theoretically, with the aid of numerical methods, that a highly chiral nematic liquid crystal can accommodate a quasi-two-dimensional Skyrmion lattice as a thermodynamically stable state, when it is confined to a thin film between two parallel surfaces imposing normal alignment. A chiral nematic liquid crystal film can thus serve as a model Skyrmion system, allowing direct investigation of their structural properties by a variety of optical techniques at room temperatures that are less demanding than Skyrmion systems discussed previously.
Similar content being viewed by others
Introduction
Skyrme showed that particle-like topological excitations can be stable in certain types of continuous nonlinear fields, and can account for the existence of protons and neutrons in the field of pions1. When one considers a continuous vector field m in three dimensions of fixed magnitude (that is, m ∈ S2), a Skyrmion is roughly understood to be a localized variation in the field, in which m rotates continuously through an angle π or π/2 (in the case of a half-Skyrmion) from its center to its boundary. Figure 1a illustrates the vector field profile of a half-Skyrmion.
(a) A Skyrmion excitation illustrated from two different viewing directions. The cylinders describe the director n. This profile is drawn from the result of our calculations presented in Figure 2a. (b) A double-twist cylinder. The director field twists in all directions perpendicular to the vertical axis of the double-twist cylinder. (c, d) Arrangements of double-twist cylinders (axes are shown by green lines) and defect lines (red) in unit cells of (c) BP I and (d) BP II.
Although the original idea of Skyrme was applied to a continuous field of pions to explain the existence of protons and neutrons1 as mentioned above, Skyrmions have found a place in a wide variety of fields of physics, in particular in condensed matter systems. In the mid-1990 s Skyrmions were predicted and observed in quantum Hall devices2,3,4, with the realization that quantum effects are best understood in terms of topological features. Later, spinor Bose–Einstein condensates were shown to accommodate Skyrmions due to the internal spin degrees of freedom5,6,7. More recently, great attention has been paid to Skyrmions in helical ferromagnets8, such as MnSi4,9,10 and Fe1-xCoxSi11,12, characterized by a lack of inversion symmetry (chirality) and the presence of Dzyalonshinskii-Moriya spin–orbit interaction. Skyrmions in chiral ferromagnets could stimulate potential applications, because local twisted magnetic structures coupled to electric or spin currents could be used to manipulate electrons and their spins.
Among the intriguing features of helical ferromagnets is their similarity9,13,14 to cholesteric blue phases (BPs) in chiral liquid crystals15. BPs have attracted much interest as one of the fascinating non-trivial structures in condensed matter systems, where the unit vector n, known as the director that denotes the average orientation of liquid crystal molecules, exhibits three-dimensional ordering. The delicate balance between the local preference for a double-twist structure over a single-twist in a helical phase and the global topological constraint that prevents a double-twist structure from filliing the whole space without introducing discontinuities yields three-dimensional regular stacks of so-called double-twist cylinders15 (Fig. 1b) and topological defect lines15. In Figure 1c and d, we show the structures of bulk BPs with cubic symmetry. BP I in Figure 1c is characterized by a space group O8 (I4132), and contains straight defect lines that do not intersect each other. Defect lines in BP II (Fig. 1d, space group O2 or P4232) form a double-diamond structure with an array of four-arm junctions. Double-twist cylinders can be regarded as a type of Skyrmion excitation with π/4 rotation. A π/4 rotation enables the n field to remain continuous at the point of contact between two neighbouring orthogonal double-twist cylinders. Possibly due to the delicate balance mentioned above, most liquid crystals exhibiting a BP have a limited stability range in temperature as small as a few Kelvin or less. However, recently discovered polymer-stabilized BPs allow a temperature range wider than 60 K16, which has stimulated numerous experimental studies aimed at practical applications of BPs such as fast-switching displays. Close similarity is apparent in the free energy densities, which take the form of a(∇×a) that is allowed in the absence of inversion symmetry8,15, where a=n (director) in the case of liquid crystals and a=m (magnetization) in the case of ferromagnets. Possible ferromagnetic structures consisting of stacks of double-twist cylinders have also been discussed9,14.
Here we show theoretically, with the aid of numerical calculations, that a highly chiral liquid crystal can be host to a stable quasi-two-dimensional (2D) Skyrmion lattice when it is confined to a thin film between two parallel plates imposing normal alignment (anchoring) at the surfaces. It should be stressed that liquid crystals possess head–tail symmetry, thus n is equivalent to −n; therefore, in comparison with magnets, they allow for a wider variety of ordered structures. Our present study is motivated by our discovery of a wide variety of ordered structures in a confined chiral liquid crystal17,18, and a very recent real-space observation of regular Skyrmion lattices in a thin film of Fe1-xCoxSi12. With the aid of extensive numerical calculations, we construct a phase diagram in terms of temperature and film thickness, and demonstrate that regular quasi-2D Skyrmion lattices with hexagonal or rectangular symmetry are indeed thermodynamically stable over a certain range of temperatures and film thicknesses.
Results
Skyrmion structures
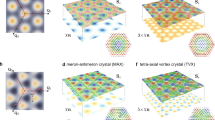
Calculations are carried out in the temperature range −1.05 K<T−T*<0.32 K, and the film thickness range 50 nm<d<200 nm. Here T* is the temperature below which an isotropic phase becomes unstable to any small perturbations. Details of our calculations are described in Methods. We present several thermodynamically stable profiles in our calculations in Figure 2a–f. Here, the director (n) profile at z=d/2 (midplane of the system) and topological defects are depicted. Confining surfaces with strong normal anchoring no longer allow straight defect lines to exist, in contrast to bulk BPs, thus yielding various exotic ordered structures not found in bulk liquid crystals. In our previous study at a fixed temperature17,18, we reported the observation of an array of double-helix defect lines (Fig. 2e) or inchworm-like fragmented defects (Fig. 2f). By varying the temperature, we find a much wider variety of ordered structures as shown in Figure 2a–d. Particularly interesting are those with hexagonal symmetry (Fig. 2a,b). In the case of small d (Fig. 2a), a 2D lattice of half-Skyrmion excitations (Fig. 1a) embedded in an array of straight topological defect lines is clearly observed, resembling those found in a recent real-space observation of thin chiral ferromagnets12. With increasing d, variation of the profile in the z-direction is allowed, which results in further exotic structures (Fig. 2b–d). The profile in Figure 2c can also be regarded as a Skyrmion lattice because half-Skyrmion excitations are still clearly visible as a centered-rectangular lattice in an array of topological defects. In Figure 2b, a labyrinth of topological defects with hexagonal symmetry prevents the formation of Skyrmion excitations. Although possible similar hexagonal structures in chiral liquid crystals have been discussed before19,20,21,22, they are bulk structures (without confinement) under an electric field; the difference between the local nature of the surface anchoring and the long-range nature of the electric field should be stressed. Moreover, the confinement does not allow screw axes to arise17, which are required for some observed and proposed bulk hexagonal structures19,20,21,22. Indeed, structures seen in Figure 2b and f cannot exist as bulk ones. It is interesting to note that in Figure 2d, four-arm junctions of topological defects can be seen clearly, reminiscent of those in BP II (Fig. 1d). Here, and also in Figure 2e and f, half-Skyrmion excitations forming a rectangular lattice can be observed. Typical lattice constants are 113 nm for the hexagonal structure of Figure 2a, and 91×101 nm for the centered-rectangular structure of Figure 2d. The dependence of the lattice constant on the temperature and film thickness is not strong; in the case of Figure 2a, the lattice constant ranges from 106 to 120 nm. Smaller film thicknesses and lower temperatures yield a larger lattice constant.
(a) Quasi-2D Skyrmion lattice with hexagonal symmetry embedded in an array of topological defects (T−T*=0 K, d=102 nm). (b) Another structure with hexagonal symmetry (T−T*=0 K, d=153 nm). (c) 2D Skyrmion lattice with centered-rectangular symmetry embedded in an array of topological defects (T−T*=0.21 K, d=153 nm). (d) 2D Skyrmion lattice with rectangular symmetry with an array of defect lines with four-arm junctions (T−T*=−0.63 K, d=179 nm). (e) 2D Skyrmion lattice with a parallel array of defect lines of double-helix form (T−T*=−0.63 K, d=153 nm). (f) Structure with inchworm-like fragmented defect lines (T−T*=−0.63 K, d=128 nm). The cylinders describe the profile of the director n, the eigenvector of Qij with the largest eigenvalue. Skyrmion excitations are emphasized by blue circles. The position of topological defects, with weaker orientational order, is specified by the isosurfaces of TrQ2=QijQij depicted in red. The values of TrQ2 at the isosurfaces are 0.08 for a and b, 0.02 for c, and 0.20 for d, e and f. Note that for the clarity of presentation, the isosurfaces are not drawn in the vicinity of confining surfaces. (g) Phase diagram with respect to temperature and film thickness. Blue circle and magenta open square correspond to NA and uniform lying helix, respectively (see text). Green cross, red-filled circle, orange triangle, blue asterisk, orange cross, and cyan-filled square correspond to the structures in a , b, c, d, e and f respectively. Grey-filled triangle represents a structure, not discussed in the main text, with centered-rectangular symmetry and no Skrymions observed from the z-direction. The positions of alphabets a–f indicate the film thickness and temperature for a to f.
Phase diagram
In Figure 2g, we present the phase diagram with respect to temperature T and film thickness d. For higher temperatures, that is, T−T*>0.25 K, an alignment normal to the confining surfaces with reduced ordering in the middle of the system is the most stable state (we will refer to this state as NA or 'normal alignment'). Note that the orientational order in the NA state is induced by confining surfaces23; the temperature is too high to allow orientational order in the bulk. In the case of a lower temperature or small d, a helical orientational order corresponding to a cholesteric phase, whose pitch is parallel to the confining surfaces, attains thermodynamic stability (often referred to as 'uniform lying helix'). In between the normal alignment state and uniform lying helix, structures presented in Figure 2a–f can be thermodynamically stable. For smaller d, a 2D hexagonal Skyrmion lattice (Fig. 2a) is energetically preferable. For larger d, thermodynamic stability of hexagonal structures (Fig. 2b) and rectangular structures (Fig. 2d,e) depends on temperature; the former is more stable for higher temperatures. The stable regions for centered-rectangular structures (Fig. 2c) and for fragmented defects (Fig. 2f) are limited in extent.
Discussion
Here we discuss the similarities and differences between the 2D hexagonal Skyrmion lattice in Figure 2a and the square one in ref. 8. In both systems, half-Skyrmion excitations are embedded in a regular lattice of topological defects. The vectorial nature of the magnetization in the latter allows only Skyrmions with +z magnetization to neighbour ones with −z magnetization; otherwise, the boundary between two Skyrmions must be discontinuous. Therefore, a hexagonal lattice is prohibited because it would lead to frustrations. For a hexagonal Skyrmion lattice to exist, Skyrmions with +z magnetization must adopt a rotation of m in the sea of −z magnetization10,12. On the other hand, in liquid crystalline systems with n and –n symmetry, such frustrations do not exist, which allows for the formation of a hexagonal lattice of half-Skyrmions.
From the phase diagram presented in Figure 2g, it is clear that if one wishes to observe 2D hexagonal Skyrmion lattices, the temperature must be carefully controlled within a range of 0.5 K at most, just as BPs in the bulk are in most cases stable over a 1 K temperature range15. The stable temperature range of rectangular Skyrmion lattices is relatively large, compared with hexagonal lattices.
We find from a separate calculation that the thermodynamic stability of 2D hexagonal Skyrmion lattices is significantly reduced when the chirality of the liquid crystal is lower (larger cholesteric pitch). This observation corresponds to the well-known fact that cholesteric BPs can be found only in highly chiral liquid crystals15. Notice also that with weak surface anchoring, a structure similar to a bulk BP is the most stable17, because the surfaces disturb only slightly the bulk structure. Together with the phase diagram in Figure 2g, we conclude that for the observation of 2D Skyrmion lattices in a chiral nematic liquid crystalline system, the following conditions must be fulfilled: high chirality; accurate temperature control (close to the transition towards the isotropic phase); and very small film thickness with strong surface anchoring.
Finally, we comment on the possibility of observing the structures discussed here experimentally. The transition from a rectangular to a hexagonal structure induced by a temperature change would be clearly detected by scattering experiments. Transmission electron microscopy with a freeze fracture technique24 could help identify the orientational profile of a confined liquid crystal together with its spatial symmetry. A more recent and promising technique that allows real-space observation is confocal microscopy, which has been applied to observe a bulk BP25, and defect structures in simple nematics and cholesterics26. We note that liquid crystals have been exploited for modelling physical systems that are difficult to access experimentally and in which topology has a substantial role27,28. Experimental observation of liquid crystalline Skyrmion systems could also shed light on the properties of other experimentally demanding Skyrmion systems, for example, 2D electron gases exhibiting quantum Hall effect, spinor Bose–Einstein condensates and chiral ferromagnets, and clarify the similarities and differences between these systems. We thus encourage experimental studies for the observation of Skyrmion lattices in a liquid crystal. Further theoretical studies may be devoted to several interesting but challenging problems on, say, the dynamics of phase transitions induced by temperature change, and possible effects of thermal fluctuations on the stability of Skyrmion structures10. We further note that photopolymerization, which was applied to the stabilization of BPs16, could open a route to various Skyrmion structures stable over a wide temperature range. The Skyrmion structures could be templates for assembling complex structures of colloidal particles that can be further stabilized by photopolymerization for possible photonic applications.
Methods
Order parameter and the Landau–de Gennes theory
Our calculations are based on a Landau–de Gennes theory describing the orientational order in terms of a symmetric and traceless tensor Qij, with i and j representing the Cartesian coordinates x, y and z. When the liquid crystal is in an isotropic state, Qij=0. In the case of uniaxial ordering, Qij=Q(ninj–(1/3)δij), where Q describes the degree of orientational order, and ni is the i-th component of the director. The local free energy density in the bulk flocal and the elastic energy fel are written as expansions in Qij and its gradients, up to the lowest relevant order, as15


Here summations over repeated indices are implied, and a, b, c are material parameters assumed to be positive. Below the temperature T*, an isotropic state becomes unstable with respect to small perturbations. ɛikl is the Levi-Civita symbol, K1 and K0 are elastic constants, and 2π/|q0| is the pitch of the cholesteric helix. For the free energy density of the confining surfaces, which we assume to impose normal alignment (anchoring), we employ the following quadratic form29

where W is the anchoring strength, and  is the order parameter preferred by the surface, with ν being the surface normal vector and Q0 being the degree of surface order. In this study, Q0 is chosen such that (Qs)ij minimizes flocal for T=T*.
is the order parameter preferred by the surface, with ν being the surface normal vector and Q0 being the degree of surface order. In this study, Q0 is chosen such that (Qs)ij minimizes flocal for T=T*.
Calculation of the orientation profile
We consider a thin film of a liquid crystal confined by two parallel flat surfaces separated by a distance d. When we take the z axis normal to the surfaces, the total free energy F is given by  . To obtain the orientational order profile minimizing F numerically, we relax not only the order parameter Qij but also the shape and size of the numerical system (imposing periodic boundary conditions in the xy plane), using the procedures described in refs 17,18 and 30. We choose typical material parameters18 a=8.0×104 J m−3, b=5.0×104 J m−3, c=3.0×104 J m−3 K−1, K1=K0=10 pN. We set the rescaled strength of chirality
. To obtain the orientational order profile minimizing F numerically, we relax not only the order parameter Qij but also the shape and size of the numerical system (imposing periodic boundary conditions in the xy plane), using the procedures described in refs 17,18 and 30. We choose typical material parameters18 a=8.0×104 J m−3, b=5.0×104 J m−3, c=3.0×104 J m−3 K−1, K1=K0=10 pN. We set the rescaled strength of chirality  to 0.7, and the rescaled anchoring strength w=2q0(a/b2)W to 2.5, corresponding to choosing 2π/|q0|≃161 nm (cholesteric pitch), and W≃1.0×10−3 J m−2 (anchoring strength). Thus, we are considering high chirality and strong surface anchoring, but these values are experimentally achievable, and are expected to maximize frustrations that will give rise to a rich variety of exotic ordered structures.
to 0.7, and the rescaled anchoring strength w=2q0(a/b2)W to 2.5, corresponding to choosing 2π/|q0|≃161 nm (cholesteric pitch), and W≃1.0×10−3 J m−2 (anchoring strength). Thus, we are considering high chirality and strong surface anchoring, but these values are experimentally achievable, and are expected to maximize frustrations that will give rise to a rich variety of exotic ordered structures.
Additional information
How to cite this article: Fukuda, J. & Žumer, S. Quasi-two-dimensional Skyrmion lattices in a chiral nematic liquid crystal. Nat. Commun. 2:246 doi: 10.1038/ncomms1250 (2011).
References
Skyrme, T. A unified field theory of mesons and baryons. Nucl. Phys. 31, 556–569 (1962).
Brey, L., Fertig, H. A., Côté, R. & MacDonald, A. H. Skyrme crystal in a two-dimensional electron gas. Phys. Rev. Lett. 75, 2562–2565 (1995).
Schmeller, A., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Evidence for Skyrmions and single spin flips in the integer quantized hall effect. Phys. Rev. Lett. 75, 4290–4293 (1995).
Neubauer, A. et al. Topological hall effect in the a phase of MnSi. Phys. Rev. Lett. 102, 186602 (2009).
Ho, T. L. Spinor Bose condensates in optical traps. Phys. Rev. Lett. 81, 742–745 (1998).
Al Khawaja, U. & Stoof, H. Skyrmions in a ferromagnetic Bose-Einstein condensate. Nature 411, 918–920 (2001).
Leslie, L. S. et al. Creation and detection of Skyrmions in a Bose-Einstein condensate. Phys. Rev. Lett. 103, 250401 (2009).
Rößler, U. K., Bogdanov, A. N. & Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 442, 797–801 (2006).
Binz, B., Vishwanath, A. & Aji, V. Theory of the helical spin crystal: a candidate for the partially ordered state of MnSi. Phys. Rev. Lett. 96, 207202 (2006).
Mühlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915–919 (2009).
Münzer, W. et al. Skyrmion lattice in the doped semiconductor Fe1-xCoxSi. Phys. Rev. B 81, 041203(R) (2010).
Yu, X. Z. et al. Real-space observation of a two-dimensional Skyrmion crystal. Nature 465, 901–904 (2010).
Tewari, S., Belitz, D. & Kirkpatrick, T. R. Blue quantum fog: chiral condensation in quantum helimagnets. Phys. Rev. Lett. 96, 042703 (2006).
Fischer, I., Shah, N. & Rosch, A. Crystalline phases in chiral ferromagnets: destabilization of helical order. Phys. Rev. B 77, 024415 (2008).
Wright, D. C. & Mermin, N. D. Crystalline liquids: the blue phases. Rev. Mod. Phys. 61, 385–432 (1989).
Kikuchi, H., Yokota, M., Hisakado, Y., Yang, H. & Kajiyama, T. Polymer-stabilized liquid crystal blue phases. Nat. Mater. 1, 64–68 (2002).
Fukuda, J. & Žumer, S. Novel defect structures in a strongly confined liquid-crystalline blue phase. Phys. Rev. Lett. 104, 017801 (2010).
Fukuda, J. & Žumer, S. Cholesteric blue phases: effect of strong confinement. Liq. Cryst. 37, 875–882 (2010).
Hornreich, R. M., Kugler, M. & Shtrikman, S. Possibility of a field-induced hexagonal blue phase in cholesteric liquid crystals. Phys. Rev. Lett. 54, 2099–2012 (1985).
Hornreich, R. M. & Shtrikman, S. Hexagonal cholesteric blue phases. Liq. Cryst. 5, 777–789 (1989).
Kitzerow, H.- S. The Effect of electric fields on blue phases. Mol. Cryst. Liq. Cryst. 202, 51–83 (1991).
Henrich, O., Marenduzzo, D., Stratford, K. & Cates, M. E. Thermodynamics of blue phases in electric fields. Phys. Rev. E 81, 031706 (2010).
Sheng, P. Boundary-layer phase transition in nematic liquid crystals. Phys. Rev. A 26, 1610–1617 (1982).
Costello, M. J., Meiboom, S. & Sammon, M. Electron microscopy of a cholesteric liquid crystal and its blue phase. Phys. Rev. A 29, 2957–2959 (1984).
Higashitani, K., Yasui, K. & Kikuchi, H. Direct observation of polymer-stabilized blue phase I structure with confocal laser scanning microscope. J. Am. Chem. Soc. 130, 6326–6327 (2008).
Smalyukh, I. I., Lansac, Y., Clark, N. A. & Trivedi, R. P. Three-dimensional structure and multistable optical switching of triple-twisted particle-like excitations in anisotropic fluids. Nat. Mater. 9, 139–145 (2010).
Chuang, I., Durrer, R., Turok, N. & Yurke, B. Cosmology in the laboratory: defect dynamics in liquid crystals. Science 251, 1336–1342 (1991).
Bowick, M. J., Chandar, L., Schiff, E. A. & Srivastava, A. M. The cosmological Kibble mechanism in the laboratory: string formation in liquid crystals. Science 263, 943–945 (1994).
Nobili, M. & Durand, G. Disorientation-induced disordering at a nematic-liquid-crystal–solid interface. Phys. Rev. A 46, R6174–R6177 (1992).
Fukuda, J., Yoneya, M. & Yokoyama, H. Simulation of cholesteric blue phases using a Landau–de Gennes theory: effect of an applied electric field. Phys. Rev. E 80, 031706 (2009).
Acknowledgements
We thank Dr Miha Ravnik for valuable discussions. Thanks are also due to Dr Richard James who critically read the manuscript and gave useful comments. J.F. appreciates financial support from the Slovenian Research Agency (ARRS research program P1-0099 and project J1-2335) and the Center of Excellence NAMASTE for his stay at the University of Ljubljana, during which most of this work was carried out. J.F. is supported in part also by KAKENHI (Grant-in-Aid for Scientific Research) on the Priority Area 'Soft Matter Physics' from the Ministry of Education, Culture, Sports, Science and Technology of Japan.
Author information
Authors and Affiliations
Contributions
S.Ž. conceived the research of a thin chiral liquid crystal film. J.F. carried out numerical calculations and analysed data. Both conceived the possibility of Skyrmion lattices in this system and discussed the results. J.F. wrote the manuscript with inputs from S.Ž.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Fukuda, Ji., Žumer, S. Quasi-two-dimensional Skyrmion lattices in a chiral nematic liquid crystal. Nat Commun 2, 246 (2011). https://doi.org/10.1038/ncomms1250
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1250
This article is cited by
-
Observation of localized magnetic plasmon skyrmions
Nature Communications (2022)
-
Spontaneous electric-polarization topology in confined ferroelectric nematics
Nature Communications (2022)
-
BPS skyrmions of generalized Skyrme model in higher dimensions
Journal of High Energy Physics (2022)
-
Autonomous materials systems from active liquid crystals
Nature Reviews Materials (2021)
-
BPS Skyrme submodels of the five-dimensional Skyrme model
Journal of High Energy Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.