Abstract
Subwavelength metallic slit arrays have been shown to exhibit extraordinary optical transmission, whereby tunnelling surface plasmonic waves constructively interfere to create large forward light propagation. The intricate balancing needed for this interference to occur allows for resonant transmission to be highly sensitive to changes in the environment. Here we demonstrate that extraordinary optical transmission resonance can be coupled to electrostatically tunable graphene plasmonic ribbons to create electrostatic modulation of mid-infrared light. Absorption in graphene plasmonic ribbons situated inside metallic slits can efficiently block the coupling channel for resonant transmission, leading to a suppression of transmission. Full-wave simulations predict a transmission modulation of 95.7% via this mechanism. Experimental measurements reveal a modulation efficiency of 28.6% in transmission at 1,397 cm−1, corresponding to a 2.67-fold improvement over transmission without a metallic slit array. This work paves the way for enhancing light modulation in graphene plasmonics by employing noble metal plasmonic structures.
Similar content being viewed by others
Introduction
Significant efforts have been made in the past 5 years to create graphene plasmon-based optical modulators that function from THz to mid-infrared frequencies. These devices have exploited the unique plasmon dispersion relation of graphene, which exhibits optical modes with high-confinement factors1,2,3,4,5,6, and that are electrostatically tunable7,8. Typically, these devices have been based on geometries that employ resonant absorption in graphene nanostructures that have been patterned to confine plasmonic modes that can be electrostatically tuned to control the intensity and frequency of either optical absorption or emission9,10,11,12,13,14,15,16,17,18,19,20,21,22. However, the single-layer atomic thickness and low free carrier density of graphene has limited the efficiencies of such modulators, especially at mid-infrared frequencies, where the oscillator strength of the graphene plasmonic modes is low. A number of strategies have been adopted to overcome these difficulties, including using ionic gel or chemical doping to increase the carrier density of the graphene sheet12,13,23,24, or carefully controlling the substrate to include a metallic back reflector, which creates additional optical resonances that enhance field intensities at the graphene plasmonic ribbons (GPRs)18,19,20,23, and thus enhance absorption. While those techniques can have theoretical modulation efficiencies of 100%, the use of ionic gels places significant restraints on the applicability, switching speeds, and durability of such devices, and the use of metallic reflectors forces those devices to be used in reflection geometries. In contrast to the reflective-type graphene plasmonic modulators, a strategy of using electrostatically tunable graphene plasmons to modulate transmitted light with near-unity efficiency has not yet been reported, to the best of our knowledge. The creation of such a device would have widespread applications in optoelectronic devices such as mid-infrared spatial light modulators, or linear signal processing25,26,27.
In this paper, we report an approach to use graphene plasmonic modes for light modulation in a transmission geometry that satisfies the above conditions—high modulation efficiency, at carrier densities accessible with electrostatic gating. Our modulator design is based on a triple resonant structure, where the plasmonic resonances in GPR are matched to a dielectric substrate Fabry–Perot resonance, and also to the optical resonances in a subwavelength metallic slit array, which is designed to exhibit extraordinary optical transmission (EOT) in the mid-infrared. In full-wave simulations, the proposed structure shows 95.7% modulation efficiency in transmission. We measured a mid-infrared transmission modulation efficiency of 28.6% at 1,397 cm−1, which is 2.67 times higher than that measured for an equivalent GPRs-only structure on the same supporting dielectric structure.
Results
Device geometry and light modulation mechanism
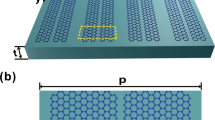
Figure 1a shows the mechanism of the proposed device. In extraordinary optical transmission, incoming light is scattered by the periodic structure into surface plasmons on the top metal surface. The surface plasmons then tunnel through the subwavelength metallic slits and excite surface plasmons on the bottom metal surface. The surface plasmon on the bottom metal surface subsequently re-radiates into free space, resulting in a transmitted diffraction peak with a strong intensity at the extraordinary optical transmission resonance frequency28,29,30,31,32,33. The subwavelength metallic slits play a pivotal role in EOT via optical coupling between the surface plasmons on the top and bottom metal surfaces. In our modulator, GPRs are placed in the subwavelength metallic slits to modulate the EOT resonant coupling. This is accomplished by electrostatically tuning the plasmonic resonances in GPRs to match the resonant frequency of the EOT. When matched, the electric fields in the subwavelength metallic slits give rise to large plasmonic resonance in the GPRs, which leads to blocking the coupling channel for the EOT resonance. As a result, a strong suppression of EOT occurs. To demonstrate this modulation mechanism, we fabricated subwavelength metallic slit array structures with GPRs on SiNx membranes, as shown in Fig. 1b,c. In Fig. 1c, the dark stripes denote the GPRs, and the bright bar corresponds to the etched region that defines the GPRs. Figure 1d shows the schematic of the equivalent GPRs-only structure on the same supporting dielectric structure as a control sample, and the SEM image of the fabricated device is shown in Fig. 1e.
(a) Schematic of the graphene plasmonic ribbons (GPRs) coupled to subwavelength metallic slit array. Under normal operation (that is, no GPRs), transverse magnetic (TM) polarized incoming light induces surface plasmons on the top metal surface (1) that tunnel through the subwavelength metallic slits (2), exciting surface plasmons (3) on the bottom metal surface. The surface plasmons on the bottom metal surface are diffracted by the periodic structure and radiate into free space with an enhanced intensity. The role of the GPRs inside the subwavelength metal slits is to block the coupling channel (4), and leading to a suppression of the extraordinary optical transmission effect. In this figure, the overlapping field distribution depicts Re(Ez) for the surface plasmons, and the scale is adjusted to fit the schematic. SEM images (false colour) of (b) the subwavelength metallic slit array and (c) the GPRs inside the subwavelength metallic slit fabricated on SiNx membrane. (d) Schematic of a transmission-type bare GPR modulator. Field distributions on the side walls correspond to Re(Ex) showing the Fabry–Perot resonance in the substrate. (e) SEM image of bare GPRs fabricated on SiNx membrane. The fabricated GPRs form a mesh to prevent electrical disconnection with 2 μm length and 100 nm bridge. The width and the gap of the GPRs are both 50 nm.
Substrate geometry optimization
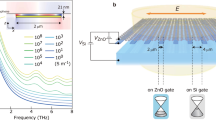
To achieve electronically tunable transmission, the substrate must be transparent at the operating frequency, yet also allow for electrostatic gating. In addition, the substrate will support Fabry–Perot-type resonances, which can lead to constructive or destructive interference effects that modify the electric field intensities on the top surface and thus the absorption in the GPRs. To satisfy these constraints, we use a SiNx membrane with a DC conducting indium tin oxide (ITO, 4nm)/a-Si (60 nm) contact on the bottom side of the membrane, as shown in Fig. 1a. To optimize the substrate thickness for maximizing absorption in GPRs, we performed full-wave simulations for an array of bare 50 nm wide GPRs, varying the SiNx thickness. The calculations were performed at λ−1=1,340 cm−1, which is the resonant frequency of 50 nm GPRs for EF=−0.465 eV, and a graphene carrier mobility (μh) of 15,000 cm2 V−1 s−1 was assumed for the graphene sheet8. Here the negative sign of EF denotes that the graphene is hole doped. As shown in Fig. 2a, the transmission spectrum exhibits a Fabry–Perot resonance that depends on the SiNx thickness (tSiNx), and leads to variation in plasmonic absorption by GPRs. In contrast to GPR reflection modulators that achieve maximum absorption at tsub=λ/4nsub (refs 19, 20), the absorption for transmission modulators has a maximum at tsub=λ/2nsub with tSiNx=2.02 μm, and the minimum occurs at tsub=λ/4nsub with tSiNx=0.87 μm (tsub: substrate thickness, tSiNx: SiNx thickness, nsub: effective refractive index of substrate). Considering this structure as a Fabry–Perot cavity, the maximal absorption point corresponds to a transmission resonance in the forward direction (also see Supplementary Fig. 1). This effect arises from the zero phase shift for light reflected from the bottom a-Si/air interface. These reflected waves constructively interfere with incident light when the reflection path length is 2tsub=λ/nsub, which corresponds to 2π in terms of the phase difference. As a result, a standing wave is formed in the substrate with a maximum on the surface, which leads to enhanced absorption in GPRs. We also observe that the near-field intensities around GPRs are enhanced at resonance, as shown in Fig. 2b,c. To further characterize the device, we calculate the spectral absorption as a function of graphene Fermi level position (EF) for a 2 μm layer of SiNx, as shown in Fig. 2d. In the absence of substrate resonances, a higher-doping level, by itself, leads to strong oscillator strength in the GPRs and thus enhances plasmonic absorption13,14,15. However, in this device the absorption is strongest at λ−1=1,340 cm−1, which occurs not for maximal doping level but when the plasmonic resonance in GPRs and substrate resonance are matched, as shown Fig. 2d. As a result, transmission declines along the plasmonic absorption in GPRs, as shown in Fig. 2e.
(a) The red line indicates absorption in the bare graphene plasmonic ribbons (GPRs) device depending on the SiNx thickness (tSiNx) with the graphene Fermi level position EF=−0.465 eV. The blue, yellow and purple lines correspond to transmittance, reflectance and absorption, respectively, depending on the SiNx thickness through the SiNx/ITO/a-Si substrate without the GPRs. Total electric field distributions around the bare GPRs at the EF=−0.465 eV with the SiNx thickness of (b) 2.02 μm and (c) 0.87 μm. (d) Absorption and (e) transmittance in the bare GPRs device as a function of frequency and EF with tSiNx=2 μm.
Theoretical modulation of coupled structure
In the proposed coupled structure, GPRs are located inside subwavelength metallic slits to modulate the coupling between the surface plasmon modes on the top and bottom metal surfaces. Four parameters dictate the subwavelength metallic slit array design: the metallic material, metal thickness, slit width, and period in transverse direction, as shown in Fig. 1a. We used Au with a thickness of 80 nm, and the subwavelength metallic slit width is 800 nm, which can support eight GPRs inside each metallic slit. For a given subwavelength metallic slit width, the EOT resonance frequency is determined by the subwavelength metallic slit array period. A period of 5.54 μm is used in simulation to match an EOT peak at λ−1=1,340 cm−1. After combining the GPRs and the subwavelength metallic slit array, the 0th order transmittance (T) as a function of frequency and EF is shown in Fig. 3a. When the plasmonic resonance in GPRs deviates from the EOT resonance frequency, the subwavelength metallic slit array exhibits resonant transmission. However, when the GPRs are gated such that plasmonic resonance in GPRs matches the EOT resonance (EF=−0.465 eV), there is a strong dip in the transmission spectrum at the crossing between two resonant modes, as shown in Fig. 3a. The total electric field distributions on and off the plasmonic resonance in GPRs are shown in Fig. 3b–e. When the plasmonic resonance in GPRs is detuned from the EOT mode, we observe a metallic surface plasmon mode on the bottom metal surface and confined fields inside the subwavelength metallic slits, indicating coupling between the two surface plasmon modes (Fig. 3b,d). In contrast, as the plasmonic resonance in GPRs is tuned to the EOT frequency (EF=−0.465 eV), both the metallic surface plasmon modes on the bottom metal surface and inside the subwavelength metallic slits are diminished significantly (Fig. 3c) because the coupling channel is blocked through interaction with the intergap GPRs (Fig. 3e). To evaluate the modulation performance, we compare modulation efficiencies of the bare GPRs and GPRs combined with the subwavelength metallic slit array (GPRs–EOT). Here, the modulation efficiency in transmittance (ηT) is defined by 1−T/Tmax, where T is transmittance as a function of EF, and Tmax corresponds to the transmission spectrum for the graphene Fermi level position that maximizes the transmitted intensity at the resonant frequency. In this simulation for GPRs, Tmax occurs at EF=−0.310 eV, where there is sufficient doping to prevent graphene inter-band absorption, but insufficient carrier density to support plasmonic modes in the GPRs. Figure 3f shows that, for high carrier mobility graphene (μh=15,000 cm2 V−1 s−1), the coupled structure shows a moderate improvement over the bare GPRs, with the theoretical maximum modulation efficiency increasing from ηT=74.5–95.7%. As the graphene carrier mobility is lowered, the overall modulation efficiency decreases in both devices. However, the relative benefits of the GPRs–EOT structure are enhanced with lower graphene carrier mobility, as shown in Fig. 3g (also see Supplementary Fig. 2). For example, at μh=3,000 cm2 V−1 s−1 the modulation efficiency of the bare GPRs is 50.6%, while the GPRs-EOT structure achieves 85.9% efficiency, and for μh=1,000 cm2 V−1 s−1 these values change to 27.3% and 65.2%, respectively. Thus the GPRs-EOT structure can exhibit large transmission modulation and is more robust against ribbon disorder compared with bare GPR-based devices.
(a) Transmittance map exhibiting graphene plasmon (GP) absorption and extraordinary optical transmission (EOT) as a function of frequency and graphene Fermi level (EF). (b–e) Total electric field distributions when turning the graphene plasmons off (EF=0 eV) and on (EF=−0.465 eV) at λ−1=1,340 cm−1. (f) Comparison of modulation efficiency in transmission (ηT) at λ−1=1,340 cm−1 as a function of EF between the bare graphene plasmonic ribbons (GPRs) and the GPRs coupled to an extraordinary optical transmission structure (GPRs–EOT). (g) Maximum modulation efficiency in transmission of bare GPRs and GPRs–EOT as a function of graphene carrier mobility (μh). The enhancement factor is calculated from the ratio of the maximum modulation efficiencies. (h) Anti-crossing behaviour (red line) by strong coupling between the EOT resonance without GPRs (blue line) and the resonance in bare GPRs (yellow line).
Modulation can be interpreted qualitatively using an effective medium theory that considers plasmonic modes in the subwavelength metallic slit array coupled to deeply subwavelength GPRs. There is significant spatial overlap between the plasmonic modes in GPRs and the EOT modes of the subwavelength metallic slit array, such that plasmonic resonances in GPRs can alter the local dielectric environment experienced by EOT modes when the two frequencies approach one another. For EF values far above or far below −0.465 eV, resonant absorption of the GPRs is far away from the transmission resonance of the subwavelength metallic slit array, and the two effects effectively behave independently. As EF approaches −0.465 eV, however, the plasmonic resonance in GPRs creates large deviations in the local dielectric function near the energy of the EOT mode. Specifically, at energies just below or above the plasmonic resonance in GPRs, the effective permittivity is increased or decreased, respectively. This allows the subwavelength metallic slit array to support two distinct modes, even though its geometry selects for only one wave vector. That is, a longer wavelength mode exists which experiences a larger permittivity, and a shorter wavelength mode exists which experiences a smaller permittivity. This creates the splitting, or anti-crossing behaviour between the graphene plasmonic resonant mode and the EOT resonant mode, as observed in Fig. 3h (also see Supplementary Note 1), and the coupling strength between the EOT structure and the embedded GPRs can be determined from the frequency splitting.
As shown in Fig. 3h, the frequency splitting is larger than the linewidth of each of the two resonant modes. This indicates that the energy exchange rate between the two resonant modes is faster than the damping rate of each mode, which suggests that the GPRs–EOT device is operating in the strong coupling regime34. The strong coupling nature of this device is further confirmed by modelling the frequency splitting as a function of graphene ribbon density, from which we find a square root relationship35,36 (Supplementary Fig. 3). As the graphene carrier mobility is lowered, the Q-factor of the GPRs decreases, and this anti-crossing behavior is lost34 (Supplementary Fig. 4). In this regime (with μh≤1,000 cm2 V−1 s−1), the GPRs–EOT modulator still displays relatively high efficiencies, but the modulation is achieved by absorption in the GPRs, where the optical modes decay too rapidly to interact strongly with the EOT structure. Notably, the modulation enhancement of the GPRs–EOT device over the bare GPRs device becomes more significant in this damping-dominant regime. Therefore we suggest that coupling between the two resonant modes is the dominant mechanism for light modulation for high carrier mobility graphene (or equivalently a high Q-factor in the graphene plasmonic resonant mode), while the GPRs with low carrier mobility graphene simply damp the EOT mode.
Mid-infrared transmission measurement
To demonstrate the modulator performance, we fabricated bare GPRs and GPRs–EOT on 2 μm SiNx membranes. First, a transparent back gate electrode composed of 4 nm of ITO and 60 nm of a-Si was sputtered onto the bottom side of the SiNx membrane. Since this back electrode is directly connected to the Si frame of the SiNx membrane, we can apply a gating voltage through the Si frame10,17,19. After transferring CVD-grown graphene to the top surface (see Methods, Supplementary Note 2 and Supplementary Fig. 5), the GPRs were patterned using e-beam lithography followed by reactive ion etching. Finally, we defined subwavelength metallic slit arrays by electron beam lithography and metal evaporation (Ti 3 nm, Au 80 nm). The slit width is 800 nm, and the period of the slit array is 5.6 μm, which puts the EOT peak at λ−1=1,403 cm−1 with undoped graphene in a mid-infrared transmission measurement. Transmission measurements were performed using a Fourier transform infrared (FTIR) microscope with a polarizer to eliminate the transverse electric component from the incoming light.
Figure 4 compares the experimentally measured transmission spectra and modulation features of bare GPRs and GPRs–EOT devices. As shown in Fig. 4a,c, both devices display gate-dependent transmission features that become stronger and shift to higher energies with increased graphene doping. To calculate and compare the modulation efficiencies, transmission spectra are normalized by the transmission spectrum with EF=−0.294 eV for bare GPRs device and EF=−0.353 eV for GPRs–EOT device, corresponding to graphene Fermi levels that exhibit maximum transmittance at the EOT resonance frequency. The resulting gate-dependent modulation efficiencies in transmission are shown in Fig. 4b,d. Both devices exhibit narrowband modulation features that become more intense and blue shift with higher graphene doping. The subwavelength metallic slit array exhibits an EOT peak at λ−1=1,403 cm−1 where no plasmons exist in the GPRs because of low doping, as shown in Fig. 4c. As doping increases, plasmons are excited in the GPRs inside the subwavelength metallic slits, and block the coupling channel for the EOT resonance. As a result, we observe the transmittance at the EOT peak decline until EF reaches −0.542 eV, which corresponds to the crossing point between the EOT resonance and the plasmonic resonance in GPRs. Figure 4e summarizes the modulation efficiencies of bare GPRs and GPRs-EOT devices. At λ−1=1,397 cm−1, the GPRs–EOT device shows maximal modulation efficiency of 28.6% with EF=−0.542 eV, while the bare GPRs device has a maximum modulation efficiency of only 10.7% at the same EF.
(a) Measured transmission spectra and (b) modulation efficiency (ηT) of the bare graphene plasmonic ribbons (GPRs) device for varying graphene Fermi level EF (or gate voltage Vg). (c) Measured transmission spectra and (d) modulation efficiency (ηT) of the graphene plasmonic ribbons coupled to extraordinary optical transmission structure (GPRs–EOT) device for varying graphene Fermi level EF (or gate voltage Vg). The legends for a–d are shown on the right side of b. (e) Measured modulation efficiency comparison at λ−1=1,397 cm−1 as a function of EF between bare GPRs device and GPRs–EOT device.
Discussion
The experimental measurements shown in Fig. 4 differ from simulations in a number of important ways. Notably, the experimental modulation is lower than the simulated one, and the spectral width of the experimental transmission resonance is significantly broader. These features can be attributed to a number of factors that distinguish measurement from simulations. The incoming light is illuminated by a Cassegrain-type objective lens with a high numerical aperture (NA) of 0.58, which means the light incidence angle ranges from −35° to 35°. Such a broad angular distribution of incident light results in a broad transmission spectrum and lower transmittance in the EOT structure because the EOT resonance condition strongly depends on incident angle as well as the period of the subwavelength metallic slit array. To estimate the effect from the broad incidence angular distribution, we calculated transmission characteristics by superposing spectra having the incident angle from −35° to 35° with 1° intervals. In these simulations, the period of the subwavelength metallic slit array is 5.2 μm, matching the EOT resonance frequency (1,403 cm−1) in our measurements. The resulting calculated transmission spectra are shown in Fig. 5, and the superposed spectrum (solid green line) shows several differences relative to the transmission spectrum for normally incident light (dotted blue line). Specifically, the superposed spectrum reveals a broader transmission spectrum with an additional peak at higher frequency (1,618 cm−1). Moreover, the angular spread of incident light lowers the maximum theoretical transmittance of the extraordinary optical transmission structure from 42.1 to 9.32%.
Simulation results demonstrating the effect of a broad angular distribution of incoming light. Dotted lines (left axis): transmission spectra of the subwavelength metallic slit array with different incident angles (θin). Solid line (right axis): weighted sum of transmission spectra at different angles for an objective numerical aperture (NA) of 0.58.
In addition to the broad light incidence angular distribution, some imperfections in fabrication could degrade the modulation efficiency, including PMMA residue on graphene, carrier density variation in the graphene created by localized charges, a variation in the width of the GPRs resulting from lithography, edge states of the GPRs induced by the etching process, and some resonators that are electronically isolated. These imperfections result in broadening of the graphene plasmon resonance linewidth and a lower modulation efficiency compared with simulations. To account for the broad incident angular distribution and imperfections in fabrication, we tuned graphene carrier mobility and employed a scaling factor as fitting parameters to explain the linewidth and modulation efficiency (see Supplementary Note 3 and Supplementary Fig. 6). Fitting results show that a graphene carrier mobility of 450 cm2 V−1 s−1 is in good agreement with the graphene plasmon resonance linewidth, which indicates that damping was a dominant factor in the light modulation for this experiment. Simulations with scaling factors of 0.633 for the bare GPRs device and 0.734 for the GPRs–EOT device are able to fit the measurement results. With these fitting parameters, the expected modulation efficiencies with purely normally incident light are 11.4% for the bare GPRs device and 36.0% for the GPRs–EOT device.
In contrast to the decreased transmission seen here due to plasmonic absorption in the GPRs, it has been reported that transmission can increase via absorption, described as absorption-induced transparency37,38,39. In ref. 37, a nanodisk is used to extract photons from a subwavelength hole and scatter them into free space, so that light transmission is enhanced. This mechanism is possible because the nanodisk’s scattering cross-section is comparable to its absorption cross-section. Refs 38,3938,39 report that EOT structures hybridized with dye absorber layers show an increase in EOT transmission when the dye is placed inside the subwavelength holes. In those devices, the absorbing medium fills the subwavelength metallic holes, allowing for an altered in-hole propagation constant. While those effects may play some role in the transmission properties of the structure we propose here, we note that in this device the transmission is decreased as the absorbing plasmonic resonances are activated, rather than increased. In the device we demonstrate here, however, the scattering cross-section of GPRs is much smaller than their absorption cross-section due to the extreme spatial confinement20. In addition, the GPRs are located only at the bottom of the subwavelength metallic slits, making such an effect less likely. While absorption-induced transparency might be achievable in devices where the array of tunable GPRs completely fills the subwavelength metallic slits, it is difficult to experimentally realize such a device.
In summary, GPRs coupled to subwavelength metallic slit array that exhibit extraordinary optical transmission enable strong transmission modulation at mid-infrared frequencies. Light absorption in GPRs efficiently suppresses the extraordinary optical transmission resonance resulting in high modulation efficiency. Simulations indicate a transmission modulation efficiency of 95.7%. This modulation occurs with small changes in the graphene Fermi level position, within ranges that are accessible with electrostatic gating methods. Experimental mid-infrared transmission measurements of a fabricated device demonstrate that the proposed device exhibits 2.67 times higher modulation efficiency than that of a bare GPRs device. The experimental modulation efficiency could be enhanced by use of graphene with higher carrier mobility and by transmission measurements using a parallel rather than a convergent beam illumination configuration since extraordinary optical transmission resonances are quite angle-sensitive. The results illustrate the potential for coupling graphene resonances and conventional noble metal plasmon resonances to achieve transmission-type light modulation, which may be useful in, for example, actively tunable amplitude modulated infrared metasurfaces and real-time hologram systems.
Methods
Material modelling in simulation
The frequency-dependent dielectric function of SiNx was measured using mid-infrared ellipsometry (Supplementary Fig. 1b). For ITO, we used tabulated data40. In the case of a-Si, we scaled a-Si data from Palik data41 by a weighting factor of 0.88, which reflects the optical characteristic difference depending on the sputtering condition, such as temperature and RF power42. Supplementary Figure 1a shows that the simulation results and the mid-infrared transmission measurement are in good agreement with these dielectric functions. The dielectric function of Au for the subwavelength metallic slit array structure was taken from Palik data41. The dielectric function of graphene is analytically modelled as a thin layer (t=0.3 nm) having a permittivity of  . Here the dynamical surface conductivity σ is calculated by random phase approximation20,43.
. Here the dynamical surface conductivity σ is calculated by random phase approximation20,43.
CVD graphene growth
CVD graphene was grown on high-purity copper foil (Alfa Aesar, 99.9999%) at 1,000 °C for 1 hour with H2 flow rate of 50 sccm and CH4 flow rate of 1 sccm (refs 44, 45). After spin-coating PMMA on top, the copper foil was etched using an FeCl3 solution (Transene, CE-100). The PMMA/graphene layer was then rinsed in DI water and transferred onto the substrate. Finally, the PMMA layer was removed with acetone. The quality of the CVD-grown graphene was characterized by Raman spectroscopy, where a negligible D-band was observed—indicating a low defect density—and a 2D to G ratio of ∼2 confirmed the monolayer nature of the graphene sheet (Supplementary Fig. 5a). The graphene Fermi level position was determined by measuring the gate-dependent sheet resistance and assigning the resistance maximum as the charge neutral point, where the graphene Fermi level is aligned with the Dirac point. After identifying the charge neutral point (Supplementary Fig. 5b), a simple capacitor model was used to calculate the graphene Fermi level position for a given gate bias24.
Sample fabrication
The DC conducting contact (ITO 4 nm/a-Si 60 nm) was deposited on the bottom side of 2 μm SiNx membrane (Norcada, NX10500N) by RF sputtering at room temperature. The RF sputtering powers for the ITO and the a-Si were 48 W and 150 W, respectively. Both GPRs and the subwavelength metallic slit array were patterned by 100 keV electron beam lithography using a PMMA resist. The GPRs were then cut using reactive ion etching with oxygen at 80 W for 15 s, with the patterned PMMA serving as a soft etch mask. The metallic layer was deposited by electron beam evaporation of Ti (3 nm) followed by Au (80 nm).
Data availability
The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information files.
Additional information
How to cite this article: Kim, S. et al. Electronically tunable extraordinary optical transmission in graphene plasmonic ribbons coupled to subwavelength metallic slit arrays. Nat. Commun. 7:12323 doi: 10.1038/ncomms12323 (2016).
References
Alonso-González, P. et al. Controlling graphene plasmons with resonant metal antennas and spatial conductivity patterns. Science 344, 1369–1373 (2014).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 487, 82–85 (2012).
Hwang, E. H. & Sarma, S. D. Dielectric function, screening, and plasmons in two-dimensional graphene. Phys. Rev. B 75, 205418 (2007).
Gan, C. H., Chu, H. S. & Li, E. P. Synthesis of highly confined surface plasmon modes with doped graphene sheets in the midinfrared and terahertz frequencies. Phys. Rev. B 85, 125431 (2012).
Christensen, J., Manjavacas, A., Thongrattanasiri, S., Koppens, F. H. L. & García de Abajo, F. J. Graphene plasmon waveguiding and hybridization in individual and paired nanoribbons. ACS Nano 6, 431–440 (2012).
Grigorenko, A. N., Polini, M. & Novoselov, K. S. Graphene plasmonics. Nat. Photon. 6, 749–758 (2012).
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Li, Z. & Yu, N. Modulation of mid-infrared light using graphene-metal plasmonic antennas. Appl. Phys. Lett. 102, 131108 (2013).
Brar, V. W. et al. Hybrid surface-phonon-plasmon polariton modes in graphene/monolayer h-BN heterostructures. Nano Lett. 14, 3876–3880 (2014).
Fang, Z. et al. Gated tunability and hybridization of localized plasmons in nanostructured graphene. ACS Nano 7, 2388–2395 (2013).
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 6, 630–634 (2011).
Fang, Z. et al. Active tunable absorption enhancement with graphene nanodisk arrays. Nano Lett. 14, 299–304 (2014).
Yan, H. et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat. Photon. 7, 394–399 (2013).
Brar, V. W., Jang, M. S., Sherrott, M., Lopez, J. J. & Atwater, H. A. Highly confined tunable mid-infrared plasmonics in graphene nanoresonators. Nano Lett. 13, 2541–2547 (2013).
Yan, H. et al. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol. 7, 330–334 (2012).
Brar, V. W. et al. Electronic modulation of infrared radiation in graphene plasmonic resonators. Nat. Commun. 6, 7032 (2015).
Alaee, R., Farhat, M., Rockstuhl, C. & Lederer, F. A perfect absorber made of a graphene micro-ribbon metamaterial. Opt. Express 27, 28017–28024 (2012).
Jang, M. S. et al. Tunable large resonant absorption in a midinfrared graphene Salisbury screen. Phys. Rev. B 90, 165409 (2014).
Thongrattanasiri, S., Koppens, F. H. L. & García de Abajo, F. J. Complete optical absorption in periodically patterned graphene. Phys. Rev. Lett. 108, 047401 (2012).
Liu, M., Yin, X. & Zhang, X. Double-layer graphene optical modulator. Nano Lett. 12, 1482–1485 (2012).
Mousavi, S. H. et al. Inductive tuning of Fano-resonant metasurfaces using plasmonic response of graphene in the mid-infrared. Nano Lett. 13, 1111–1117 (2013).
Thareja, V. et al. Electrically tunable coherent optical absorption in graphene with ion gel. Nano Lett. 15, 1570–1576 (2015).
Das, A. et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 3, 210–215 (2008).
Genevet, P. & Capasso, F. Holographic optical metasurfaces: a review of current progress. Rep. Prog. Phys. 78, 024401 (2015).
Meinzer, N., Barnes, W. L. & Hooper, I. R. Plasmonic meta-atoms and metasurfaces. Nat. Photon. 8, 889–898 (2014).
Yu, N. & Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 13, 139–150 (2014).
Ebbesen, T. W., Lezec, H. J., Ghaemi, H. F., Thio, T. & Wolff, P. A. Extraordinary optical transmission through sub-wavelength hole arrays. Nature 391, 667–669 (1998).
Martín-Moreno, L. et al. Theory of extraordinary optical transmission through subwavelength hole arrays. Phys. Rev. Lett. 86, 1114–1117 (2001).
Pacifici, D., Lezec, H. J., Atwater, H. A. & Weiner, J. Quantitative determination of optical transmission through subwavelength slit arrays in Ag films: role of surface wave interference and local coupling between adjacent slits. Phys. Rev. B 77, 115411 (2008).
Pacifici, D., Lezec, H. J., Sweatlock, L. A., Walters, R. J. & Atwater, H. A. Universal optical transmission features in periodic and quasiperiodic hole arrays. Opt. Express 16, 9222–9238 (2008).
Porto, J. A., García-Vidal, F. J. & Pendry, J. B. Transmission resonances on metallic gratings with very narrow slits. Phys. Rev. Lett. 83, 2845–2848 (1999).
Zhang, X., Liu, H. & Zhong, Y. Microscopic analysis of surface Bloch modes on periodically perforated metal surfaces and their relation to extraordinary optical transmission. Phys. Rev. B 89, 195431 (2014).
Khitrova, G., Gibbs, H. M., Kira, M., Koch, S. W. & Scherer, A. Vacuum Rabi splitting in semiconductors. Nat. Phys. 2, 81–90 (2006).
Agarwal, G. S. Vacuum-field Rabi splittings in microwave absorption by Rydberg atoms in a cavity. Phys. Rev. Lett. 53, 1732–1734 (1984).
Rudin, S. & Reinecke, T. L. Oscillator model for vacuum Rabi splitting in microcavities. Phys. Rev. B 59, 10227–10233 (1999).
Imura, K., Ueno, K., Misawa, H. & Okamoto, H. Anomalous light transmission from plasmonic-capped nanoapertures. Nano Lett. 11, 960–965 (2011).
Hutchison, J. A., O’Carroll, D. M., Schwartz, T., Genet, C. & Ebbesen, T. W. Absorption-induced transparency. Angew. Chem. Int. Ed. 50, 2085–2089 (2011).
Rodrigo, S. G., García-Vidal, F. J. & Martín-Moreno, L. Theory of absorption-induced transparency. Phys. Rev. B 88, 155126 (2013).
Dubreuil, D., Ganne, J.-P., Berginc, G. & Terracher, F. Optical and electrical properties between 0.4 and 12 μm for Sn-doped In2O3 films by pulsed laser deposition and cathode sputtering. Appl. Opt. 46, 5709–5718 (2007).
Palik, E. D. Handbook of Optical Constants of Solids Academic Press (1998).
Pal, P. & Chandra, S. RF sputtered silicon for MEMS. J. Micromech. Microeng. 15, 1536–1546 (2005).
Falkovsky, L. A. Optical properties of grapheme. J. Phys.: Conf. Ser. 129, 012004 (2008).
Li, X. et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009).
Li, X. et al. Graphene films with large domain size by a two-step chemical vapor deposition process. Nano Lett. 10, 4328–4334 (2010).
Acknowledgements
This work was supported by US Department of Energy (DOE) Office of Science grant DE-FG02-07ER46405 (S.K. and H.A.A.), and by the Multidisciplinary University Research Initiative Grant, Air Force Office of Scientific Research MURI, grant no. FA9550-12-1-0488 (V.W.B. and M.S.J.). S.K. acknowledges support by a Samsung Scholarship. The authors thank G. Rossman for assistance with the FTIR microscope.
Author information
Authors and Affiliations
Contributions
S.K. and H.A.A. conceived the ideas. S.K., M.S.J. and K.W.M. performed the simulations. S.K. and Y.T. fabricated the sample. S.K. and V.W.B. performed measurements and data analysis. All authors co-wrote the paper, and H.A.A. supervised the project.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
Supplementary Figures 1-6, Supplementary Notes 1-3 and Supplementary References. (PDF 1798 kb)
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Kim, S., Jang, M., Brar, V. et al. Electronically tunable extraordinary optical transmission in graphene plasmonic ribbons coupled to subwavelength metallic slit arrays. Nat Commun 7, 12323 (2016). https://doi.org/10.1038/ncomms12323
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms12323
This article is cited by
-
Full 2π tunable phase modulation using avoided crossing of resonances
Nature Communications (2022)
-
Real-space imaging of acoustic plasmons in large-area graphene grown by chemical vapor deposition
Nature Communications (2021)
-
Mid-infrared radiative emission from bright hot plasmons in graphene
Nature Materials (2021)
-
Spectral Shifting in Extraordinary Optical Transmission by Polarization-Dependent Surface Plasmon Coupling
Plasmonics (2020)
-
Efficient Optical Reflection Modulation by Coupling Interband Transition of Graphene to Magnetic Resonance in Metamaterials
Nanoscale Research Letters (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.