Abstract
Much consideration has been given to the role of spin-orbit coupling (SOC) in 5d oxides, particularly on the formation of novel electronic states and manifested metal-insulator transitions (MITs). SOC plays a dominant role in 5d5 iridates (Ir4+), undergoing MITs both concurrent (pyrochlores) and separated (perovskites) from the onset of magnetic order. However, the role of SOC for other 5d configurations is less clear. For example, 5d3 (Os5+) systems are expected to have an orbital singlet with reduced effective SOC. The pyrochlore Cd2Os2O7 nonetheless exhibits a MIT entwined with magnetic order phenomenologically similar to pyrochlore iridates. Here, we resolve the magnetic structure in Cd2Os2O7 with neutron diffraction and then via resonant inelastic X-ray scattering determine the salient electronic and magnetic energy scales controlling the MIT. In particular, SOC plays a subtle role in creating the electronic ground state but drives the magnetic order and emergence of a multiple spin-flip magnetic excitation.
Similar content being viewed by others
Introduction
The diverse physics of transition metal oxides has stimulated interest for decades. Particular focus has resided on 3d oxides where the strong electron correlations dominate, with a dramatic manifestation being the occurrence of the Mott metal-insulator transition (MIT)1,2. Contrastingly in 5d oxides the relativistic spin-orbit coupling (SOC) is increased to such an extent that competition occurs with the on-site electron correlations, as well as further interactions such as the crystalline electric field (CEF), Hund’s coupling and increased orbital overlap. The consequence of these often finely balanced interactions in 5d oxides is the emergence of new physics, such as a SOC dominated jeff=1/2 Mott-like insulating state, initially observed in perovskite iridates3,4, and Weyl semi-metal, non-trivial topological insulators and magnetic MITs in pyrochlore iridates2,5,6. Considering the pyrochlore osmate Cd2Os2O7, the concomitant magnetic ordering and MIT cannot be reconciled with the Mott–Hubbard paradigm7,8,9,10,11. Instead the behaviour was initially considered to be the first manifestation of a Slater transition where the onset of magnetic order creates the insulating phase by introducing a periodic potential that localizes the conduction electrons12. More recently, however, the mechanism of the MIT has been argued to be a Lifshitz transition normally associated with metal–metal transitions and generally not explicitly requiring magnetic order7,8.
Phenomenologically the behaviour of Cd2Os2O7 is analogous to iridate pyrochlores: they both undergo temperature dependent continuous MITs suggested to be associated with all-in/all-out (AIAO) magnetic ground states where all spins either point in or out of the centre of the tetrahedron13,14,15. One consequence of the AIAO ground state is that since the ordering breaks time-reversal symmetry, but maintains the cubic symmetry of the lattice, such systems can host Weyl semi-metal behaviour5,6. Although there exists apparent similarities between osmate and iridate pyrochlores, they contain distinct electronic occupancies of 5d5 in the iridates and 5d3 in osmates. One consequence of this is the consideration of SOC in the manifested behaviour of these systems. In iridates SOC assumes an explicit role in the behaviour and is readily evidenced, for example in the creation of the jeff=1/2, 3/2 electronic ground state. However, in the osmates the influence of similarly large SOC in the creation of the electronic ground state and emergent physical behaviour is often subtle resulting in it often being neglected or considered implicitly.
Here, we consider the role of SOC in Cd2Os2O7 by accessing the electronic and magnetic ground states and the excitations that emerge. In doing so we consider both the similarities and distinctions between 5d3 and 5d5-based pyrochlore systems. We access the magnetic Os sublattice in Cd2Os2O7 with neutron powder diffraction (NPD) and confirm the AIAO magnetic structure, thereby going beyond the strong but indirect evidence presented for AIAO ordering of the Ir sublattice in the pyrochlore iridates. To uncover the salient electronic and magnetic interactions, we perform osmium L-edge resonant inelastic X-ray scattering (RIXS) that allows us to directly probe the 5d electrons and associated-microscopic interactions, and their energy hierarchy, which we benchmark against detailed theory. These measurements extend the RIXS technique to 5d materials beyond iridates, where they have provided important insights16,17,18,19,20,21,22. In Cd2Os2O7, we find electronic excitations between 5d states that are markedly different from iridates, thereby revealing a divergent and suppressed role of SOC in the creation of the electronic ground state. However, when considering higher order effects or interactions that derive from more than one Os ion, we find an elevated role of SOC in Cd2Os2O7 and similar behaviour to pyrochlore iridates. The subtle but central role of SOC is realized both in the creation of the magnetic ground state and in the observation of a magnetic excitation. The excitation emerges in Cd2Os2O7 due to the cooperation of the large SOC, single-ion anisotropy and Dzyaloshinskii–Moria (DM) interactions that combine to form a superposition of multiple spin-states from the AIAO magnetic ground state. Collectively, despite the distinct electronic ground states, the NPD and RIXS results on the 5d3-osmate Cd2Os2O7 indicate parallels with 5d5-iridate pyrochlores and the predictions of associated exotic topological insulating and Weyl semi-metal states.
Results
Magnetic ground state of Cd2Os2O7 resolved with NPD
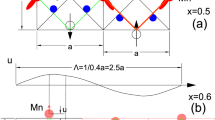
The specific type of magnetic structure adopted on the frustrated pyrochlore lattice is predicted to play a crucial role in the potential Weyl semi-metal state in the pyrochlore iridates and the magnetic MIT in Cd2Os2O7. The magnetic ground state in Cd2Os2O7 has been shown to be consistent with the AIAO ordering8, however, as with the predictions of AIAO ordering on the pyrochlore iridates this relied on some conjecture on the basis of structural arguments. Experimentally both iridium and cadmium-based compounds suffer from strong neutron absorption and coupled with small magnetic moments, this has prohibited the successful observation of magnetic Bragg peaks from the 5d ions in either iridate or osmate pyrochlores with NPD. To overcome this, we prepared a Cd2Os2O7 powder sample with isotopic 114Cd that can be measured with NPD with negligible neutron absorption. The results of NPD measurements are shown in Fig. 1a. We modelled the data with the allowed irreducible representations (Γ) for a q=0 propagation vector and the Os ion at the 16c Wyckoff site of (0,0,0) (ref. 8). Only the AIAO magnetic structure model, irreducible representation Γ3, accurately fit the data, thereby confirming this as the magnetic ground state formed in Cd2Os2O7. The AIAO magnetic structure is shown in Fig. 1b. By normalizing the magnetic intensity to structural Bragg peaks, we obtained an ordered-magnetic moment of 0.59(8)μB/Os. This is significantly reduced from the expected value for a S=3/2 system of 3 μB/Os. The presence of reduced magnetic moments has been noted in several 5d systems, and specifically those with the same 5d3 occupancy23 and is often explained in terms of the extended orbitals in 5d systems leading to an increase in hybridization and reduced local moment, and where applicable, frustration. Nevertheless, questions still remain as to whether this is in general a complete description, and specifically if SOC plays a role in the reduction. For example, do cases with a large reduction in the moment in 5d3 systems indicate an alteration of the electronic ground state away from an orbitally quenched t2g3 state into, for example, an electronic ground state similar to that found in the iridates3. In addition, an understanding of the role of SOC, particularly when combined with further effects, such as non-cubic distortions and anisotropies in the system, is required to explain the emergent physical properties out of the AIAO magnetic ground state that appears central to the behaviour in this pyrochlore osmate and related iridate pyrochlores. To gain this understanding, we performed RIXS measurements at the Os L-edge in Cd2Os2O7.
(a) NPD measurements on 114Cd2Os2O7. The 114Cd isotope was used to overcome the significant neutron absorption of Cd. The data (red circle) show the difference between measurements taken at 240 and 160 K and was fit with an all-in/all-out magnetic structural model (black line). The blue line is the difference between the measurement and magnetic model. (Inset) The (220) magnetic reflection intensity, 2θ=39.1°, shows magnetic ordering occurs at TN=225 K. The error on the data represents the square root of the measured counts. The red line is a guide to the eye derived from a least squares fit to a power law. (b) The spins (blue arrows) all point in or out of the centre of the tetrahedron forming the all-in/all-out magnetic structure in Cd2Os2O7. The bonds between Os ions forming the tetrahedra are shown as solid lines.
RIXS measurements of Cd2Os2O7 at the osmium L3-edge
The results for RIXS measurements at fixed incident energy at the Os resonant edge energy of 10.877 KeV are shown in Fig. 2a. Two pronounced features are evident, labelled EB and EC, each significantly broader than the experimental energy resolution and centred at EB=0.92(6) eV and EC=4.5(1) eV. In addition, a small, sharp resolution-limited feature EA is observed at EA=0.16(1) eV. (EA is more apparent in Fig. 3). Much can be learned by probing the intensity dependence of the inelastic spectra at different fixed incident energies, as shown in Fig. 2b. These measurements reveal features EA and EB have their maximum resonant intensity at the same incident energy, 10.8755(5) keV, whereas EC has a maximum intensity at a higher incident energy of 10.879(1) keV. The resonant energies correspond to the core–hole transition energy accessed during the RIXS process18,19. For Os L-edge RIXS, the core–hole process is 2p–5d. However, the 5d manifold is nominally split into t2g and eg sub-manifolds that result in a distinction between the energies of the 2p–5d(t2g) and 2p–5d(eg) resonant processes. The scattering involving excitations within the t2g manifold will occur at a lower energy than scattering involving eg levels, with the energy difference corresponding to the t2g and eg splitting. This allows us to assign features EA and EB to intra-t2g processes and EC as involving t2g–eg processes.
(a) Fixed incident energy photons of Ei=10.877 KeV, corresponding to the osmium resonant L3-edge, probe an inelastic energy loss spectrum out to 7.5 eV (black dots). Three inelastic features are resolvable, EA=0.16(1) eV, EB=0.92(6) eV and EC=4.5(1) eV. The horizontal bars indicate the instrument resolution of 130 meV (FWHM). The full RIXS spectrum was modelled with three Gaussians fitting the inelastic peaks EA, EB and EC, and a Gaussian for the elastic signal on top of a sloping background (blue line). (b) Varying the incident energy to follow the intensity dependence of the inelastic spectra reveals the maximum resonant intensity of EA and EB occur at the same incident energy of Ei=10.8755(5) keV (solid line), whereas EC has a maximum at Ei=10.879(1) keV (dashed line). The difference of the resonant energies reflects the splitting of the osmium d-manifold, nominally into t2g and eg shells, and allows a categorization of the excitations as intra-t2g (EA and EB) or t2g−eg (EC). (c) Schematic of the initial and final RIXS process. The initial electronic ground state before exciting an electron is indicated by the red spins in the limit of cubic CEF splitting of the 5d manifold. The final RIXS states for EB (intra-t2g) and EC (t2g−eg) are indicated by the blue and green spins, respectively. All measurements were performed at 60 K at q=(2.5,8.8,8.8).
(a) RIXS spectra at constant q=(2.5,8.8,8.8) and fixed incident energy Ei=10.877 KeV at several temperatures through the magnetic MIT in Cd2Os2O7 reveals EA as a temperature dependent excitation. (b) The low-energy excitation (EA=160 meV), along with the elastic line, was fit to a Gaussian on a background from the higher energy scattering at 60 K (red diamonds) and 250 K (grey squares). (c) The intensity at EA appears and increases below the magnetic MIT temperature of 225 K, the line is a least squares fit to a power law. (d) RIXS measurements in the magnetic insulating regime at T=60 K performed along high-symmetry directions in the magnetic Brillouin zone. The elastic scattering was suppressed by measuring within 4° of 2θ=90°, the remaining elastic signal has been subtracted from the data. (Inset) The Brillouin zone in the (HKK) plane is shown (grey) and the directions measured (red). (e) The inelastic energy and (f) intensity dependence of EA reveal dispersionless behaviour for EA. Error bars throughout the figure represent the s.d. in the data fitting procedure.
5d-manifold ground state and energy scales in Cd2Os2O7
To further interpret the underlying physical processes and interactions leading to the measured RIXS spectra, we benchmark our results against recent many-body quantum chemistry calculations24. Those calculations predicted Os d–d multiplet excitations in Cd2Os2O7 starting around 1.5 eV, which overestimates the energy but is generally consistent with the measured energy for EB (we discuss this divergence more when addressing excitation EC). Moreover, this excitation is predicted to be from intra-t2g processes, agreeing with the results in Fig. 2b. In the absence of SOC and trigonal CEF distortion, EB will consist of three peaks, however, these are unresolvable. Including SOC and trigonal CEF will split these peaks further24. However, the single-broad feature of EB indicates this splitting is not appreciable. As shown schematically in Fig. 2c, this intra-t2g (t2g3→t2g3) excitation at EB can be described as corresponding to a spin flip of one of the three electrons in the 5d3 valance band at the osmium site, changing the total local spin from high-spin S=3/2 to low-spin S=1/2, and reveals information on the t2g splitting and Hund’s coupling (JH). Even considering the atomic level, these states have multi-determinant character and requires careful interpretation25. For example, to form an eigenstate the determinant shown in the Fig. 2c (↓↑↑) needs to be augmented by the (↑↓↑) determinant with a minus sign. The corresponding energy of this multi-determinant state is 3U′, while the single low-spin determinant has the energy 3U′-JH and the high-spin single-determinant state has 3U′-3JH (following the notation of ref. 25). Overall, peak EB hosts in total eight S=1/2 states (neglecting SOC and trigonal distortions to first approximation)24. Five of those have relative energy of 3JH and the remaining three have 5JH causing the average to be 3.75JH. This gives an estimate of JH=0.92 eV/3.75≈0.25 eV.
This type of Hund (spin) excitation, which has been observed in 3d oxides, has never been previously measured in a 5d system. Indeed the presence of EB immediately reveals a different d-manifold electronic ground state in Cd2Os2O7 compared to the jeff=1/2 Mott-like iridates. Specifically, Ir L-edge RIXS measurements show appreciable SOC splitting of the t2g manifold, of the order 0.4 eV in pyrochlore iridates22 in the form of a spin-orbit exciton that is absent from the RIXS spectra for Cd2Os2O7 (refs 16, 17, 18, 19, 20). The absence of a SOC-driven exciton in the RIXS spectra of Cd2Os2O7, with instead the presence of EB, strongly indicates that SOC does not appreciably split the t2g manifold, that is, the SOC-driven jeff=3/2, 1/2 electronic ground state is not realized in this 5d3 osmate.
The higher energy excitation EC involves transitions that access the eg level, as shown in Fig. 2b. Calculations predicted inter t2g-eg excitations (t2g3→t2g2eg1) at 5 eV (ref. 24), again about 0.5 eV above the observed RIXS peak indicating a consistent overestimation in the calculations. The divergence between predicted and observed excitations, at least in part, can be explained by the details of the calculations in ref. 24, where altering the number of states or description of the nearest neighbour sites in the spin-orbit treatment will affect the predicted energies. Excitation EC, shown schematically in Fig. 2c, is a direct measurement of the 10Dq CEF splitting of 4.5 eV in Cd2Os2O7. For SOC to play a role in the ground state electronic configuration it needs to intermix the t2g3 manifold itself, which our measurement of feature EB indicates does not appreciably occur, or mix it with t2g2eg1 states. However, with a large 10Dq splitting of 4.5 eV, of order 1 eV larger than that found in pyrochlore iridates22, the latter mixing is strongly prohibited.
Collectively the RIXS results for d–d transitions in Cd2Os2O7 reveal an electronic ground state of the 5d3 ion in Cd2Os2O7 that is dominated by CEF (4.5 eV) followed by Hund’s coupling (0.3 eV). The much reduced effect of SOC in the creation of the electronic ground state of the Os5+ ion, counter intuitively, is not at odds with the expectations of observable effects of the large SOC that is intrinsic to 5d systems7,11. For example, as we discuss further, the role of SOC comes to the fore when either considering excited magnetic and electronic states or when going beyond the single-ion ground state.
Momentum and temperature dependence of excitation EA
Having characterized the electronic ground state from RIXS excitations at 1 eV and above, we now focus on feature EA at 160 meV. This energy does not correspond to any expected d–d energy scale for the d3 electronic configuration in a nearly cubic CEF, see for example, ref. 26. Moreover, EA is distinct from the d–d excitations EB and EC in being much sharper in energy. Figure 3a–c shows the intensity of EA follows an order parameter-like behaviour with temperature, with EA appearing at the magnetic MIT, and remains at the same energy of 160 meV. We followed the momentum dependence, Fig. 3d,e, and conclude EA is a non-dispersive excitation, within the 130 meV experimental resolution. While the intensity of EA appears to show some variation within the Brillouin zone (Fig. 3f), this is, at least in part, an artifact of the observed variation of the elastic line as the crystal is necessarily measured in slightly different physical orientations altering the X-ray beam attenuation.
The origin and behaviour of mode EA is puzzling for a variety of reasons. Interpretation of this feature in terms of a conventional magnetic excitation appears problematic given the small calculated value of the nearest-neighbour exchange interaction J=6.4 meV for Cd2Os2O7 (ref. 24). Therefore, we first consider potential non-magnetic mechanisms. One scenario, given the concomitant MIT, is a relationship with the insulating state. Such an excitation was observed in the iridate A2IrO3 (ref. 20), with an excitation of 340 meV corresponding exactly to the Mott-gap size. A similar origin, however, is inconsistent with known behaviour of Cd2Os2O7, for which the insulating gap has been shown to open continuously, a fact that has been cited in favour of a Slater mechanism7,8. Therefore, if feature EA was related to the insulating gap, one would expect to observe a significant shift in the energy with temperature. This is not the case. Moreover, the insulating gap, 2Δ, in Cd2Os2O7 is around 100 meV (ref. 8) and is, therefore, not consistent with the measured RIXS spectra. We finally rule out a d–d excitation scenario by noting that the t2g levels are already split at high temperature (>225 K) in Cd2Os2O7, indeed this is one of the causes of the single-ion anisotropy in the system. Any alteration of the t2g splitting due to lower symmetry crystal fields below the magnetic MIT will not produce such a low-lying d–d excitation. This is supported by the RIXS measurements not showing any change in EB or EC that would indicate an altered ground state and potential routes for EA.
SOC-driven magnetic excitation
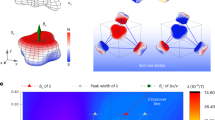
We argue that EA does indeed have a magnetic origin and support this with numerical exact diagonalisation (ED) calculations. The AIAO magnetic structure is stabilized in the frustrated pyrochlore lattice by single-ion axial anisotropy7,8,24. Therefore, in the leading approximation the spins can be considered to be Ising-like local S=3/2. In this case, the resultant classical Hamiltonian that includes easy-axis anisotropy (D), Heisenberg exchange (J) and the DM interaction (d) gives three types of local-spin excitations for this S=3/2 system of Sz=3/2→1/2 (ΔSz=1), Sz=3/2→−1/2 (ΔSz=2) and Sz=3/2→−3/2 (ΔSz=3). These have the following discrete energies:



To explore the relevance of the ΔSz processes to the RIXS data, we performed ED calculations. The ground state and all possible excited states of the Hamiltonian

with unitary vectors  and
and  were obtained for given 4-site and 8-site clusters that encompass the full AIAO magnetic ground state with a fixed parameter set reported in ref. 24, that includes d=1.7 meV, D=−6.8 meV and J=6.4 meV. The ED calculations take into account explicitly the quantum nature of the spin-states and the interactions between them, the results are shown in Fig. 4. The calculated energy shows excellent agreement with experiment. We note that the intensities calculated are the density of states (DOS) and therefore are not directly proportional to the RIXS cross section, which is non-trivial to calculate.
were obtained for given 4-site and 8-site clusters that encompass the full AIAO magnetic ground state with a fixed parameter set reported in ref. 24, that includes d=1.7 meV, D=−6.8 meV and J=6.4 meV. The ED calculations take into account explicitly the quantum nature of the spin-states and the interactions between them, the results are shown in Fig. 4. The calculated energy shows excellent agreement with experiment. We note that the intensities calculated are the density of states (DOS) and therefore are not directly proportional to the RIXS cross section, which is non-trivial to calculate.
Eight site ED calculations, including resolution broadening, showing the character and amount of excited eigenstates at a particular energy. The scaled-experimental data (black) is shown after background subtraction with error bars representing 1 s.d. The ED results reveal ΔSz=1,2,3 (Ô=S+,(S+)2,(S+)3) excitations indicated by blue, green and red, respectively. The strong SOC and consequently DM interactions in the magnetic ground state and excited states of Cd2Os2O7 result in a superposition of these ΔSz spin-states all contributing to the excitation. The calculated intensity corresponds to the DOS and therefore the actual experimental intensity distribution of the excitation measured by the RIXS cross section is likely dominated by the ΔSz=1 process, followed by ΔSz=2 and then ΔSz=3. Inset corresponds to 4-site calculations and highlights the mixing and energy distribution of the ΔSz excitations.
In the classical limit, equations (1, 2, 3), the possible spin-flip excitations for a S=3/2 system of ΔSz=1, 2, 3 have distinct energies. Conversely, the spectra for the ΔSz excitations from ED calculations are mixed and rather similar with an overlapping single-peaked excitation. The only distinction between the different ΔSz processes from ED calculations is a slight variation in energy and an overall intensity-scaling factor in their DOS, as shown by the red, green and blue regions in Fig. 4. The mixing of ΔSz=1, 2, 3 is due to quantum fluctuations leading to a superposition of different spin-states that occurs due to the DM interaction being appreciable in strength in Cd2Os2O7, J/d=3, which is in turn related to the strong SOC intrinsic in Cd2Os2O7. The DM interaction mixes states with different spin projection Sz into both the ground state and the excited states. This mixing occurs to such an extent that the separate ΔSz=1, 2, 3 excitation channels become indistinguishable and result in spectra with broad tails and a maximum of intensity very close to the energy measured for EA of 160 meV.
The strong agreement between the observed magnetic excitation energy and that predicted from ED calculations on the basis of the inclusion of the J, d and D interactions predicted in ref. 24, with essentially no free parameters, indicates that this model robustly describes the essential physics of the system. Further experimental support for the magnetic origin of excitation EA is found when recalling the RIXS incident-energy dependence (Fig. 2b). The incident energy spectra showed both EA and EB had the same incident-energy resonance dependence indicating they both involve solely intra-t2g excitations. In addition, we observed EA is non-dispersive (Fig. 3d). This is indeed expected in a system that is predominantly of Ising type, since the AIAO structure is a lowest energy, rather than degenerate, ground state, and will suppress the propagation of a flipped spin that alters the magnetic ordering.
Inspecting the ED calculations in Fig. 4 shows the prediction of the strongest DOS contribution to be from the ΔSz=3 process. Such an excitation would usually be forbidden by RIXS spin-only selection rules that limits the possible measurable excitations to ΔSz=1 and 2 (ref. 27). The ΔSz=3 process, however, becomes experimentally allowed in Cd2Os2O7 in the intermediate RIXS process due to the creation of a 5d4 state on the Os ion (2p65d3→2p55d4) where SOC will dominate. In this intermediate state S is no longer a good quantum number, therefore the standard spin-only selection rules no longer apply making a ΔSz=3 excitation allowed and measurable with RIXS. Indeed this would be the first such case of a measured excitation with a ΔSz=3 component by any experimental technique, for example neutrons carry spin-1/2 and can only measure ΔSz=0 or 1 magnetic excitations. Nevertheless, the experimental RIXS cross section will expected to be dominated by the single-magnon followed by the two-magnon processes and then the ΔSz=3 triple-magnon component.
Discussion
The NPD and Os L-edge RIXS measurements have provided direct access to the 5d electrons, competing inter and intra-ion interactions, and probed the AIAO magnetic ground state and subsequent excitations in Cd2Os2O7. The results allow a detailed and general understanding of the role of SOC and magnetism in creating the MITs in both osmate (5d3) and iridate (5d5) pyrochlores where the behaviour is phenomenologically similar, but the electronic ground state is revealed as distinctly different.
First, we consider the electronic ground state. In the 5d5 iridates, there is one hole in the t2g shell giving rise to three nearly degenerate orbital configurations carrying orbital moment leff=1 and spin S=1/2, which SOC splits into a jeff=1/2 doublet and a jeff=3/2 quartet. This splitting has been observed in several RIXS measurements as a well-defined feature termed a spin-orbit exciton16,17,22. Conversely in Cd2Os2O7, there are three valence electrons that half-fill the t2g shell. Therefore, to the leading order Cd2Os2O7 carries a spin S=3/2 and no orbital moment leff=0. The orbital moment is quenched because there is only one possible orbital configuration with three spins aligned. The RIXS spectra of Cd2Os2O7 provides direct evidence of the different ground states in 5d5 (Ir) compared to 5d3 (Os) via the measurement of excitation EB in Cd2Os2O7 that reveals a t2g manifold with no observable splitting into jeff=3/2,1/2 bands. This occurs since SOC cannot affect the half-filled t2g shell, apart from second-order effects. In this strict sense, SOC plays a negligible role in creating the electronic S=3/2 ground state in 5d3 systems. Considering second-order effects in Cd2Os2O7, the leading correction comes from the fact that the eg states, while well-separated, are not infinitely far above the t2g shell. SOC can therefore admix eg states into the t2g S=3/2 ground state. This effect is governed by the ratio of the SOC λ (∼0.4 eV) (ref. 6) and the crystal field splitting 10Dq (∼4.5 eV). The leading order result of this mixing is a single-ion magnetic anisotropy: a splitting between the Sz=+/−1/2 and the Sz=+/−3/2 projections of the S=3/2 manifold, where z is the easy axis of the system. For Cd2Os2O7 this results in an easy-axis anisotropy of around 7 meV (ref. 24). Further consequences of the SOC exist when going beyond single-site considerations, such as the DM interaction. Therefore, while SOC does not dominate the mechanisms creating the electronic ground state of a single Os ion, in contrast to the jeff=1/2 Mott-like iridates, it can still strongly impact the physics of Cd2Os2O7.
The intrinsically large SOC in Cd2Os2O7 manifests in the stabilization of the AIAO magnetic ground state that was confirmed with NPD measurements. This non-degenerate magnetic ground state is selected in the frustrated pyrochlore structure due to the single-ion anisotropy in the system. A similar mechanism is expected to exist in pyrochlore iridates, although the AIAO ordering has not been directly measured on the Ir sublattice. Nevertheless, the AIAO magnetic ordering has been the focus of considerable interest in pyrochlore iridates due to the potential for exotic phenomena including Weyl semi-metal and topological insulating behaviour2,6,13,14,15. Analogous behaviour can be mapped over to pyrochlore osmates with AIAO ordering. In terms of the observed MITs in pyrochlore iridates, the AIAO ordering is predicted to play a direct role with the existence of either concurrent or proximate magnetic ordering6. Considering the phenomenologically similar behaviour between the pyrochlore iridates and the pyrochlore osmate Cd2Os2O7 suggests an analogous underlying mechanism for the magnetic MITs. Our results indicate neither of the divergent electronic ground states adopted within the 5d3 osmate and 5d5 iridate pyrochlore systems of orbital singlet with nearly quenched effective SOC and SOC-enhanced jeff=1/2, respectively, play a dominant role with regards to creating the MITs. Instead the underlying mechanism appears directly related to the enhanced SOC in both systems that produces the strong single-ion anisotropy and subsequent AIAO magnetic ordering.
The emergence of the magnetic excitation at EA=160 meV in the RIXS measurements of Cd2Os2O7 provides a measurable manifestation for the large SOC in 5d3 systems. The existence of this excitation from the AIAO ground state was shown to be a direct consequence of the strong DM exchange interaction and single-ion axial anisotropy that couple with the comparable energy of the magnetic exchange interaction; with the concomitant behaviour necessary to create the observed magnetic excitation. The coupling of these interactions on the Ising-like AIAO ground state results in a magnetic excitation that corresponds to a superposition of multiple spin-flip processes (ΔSz=1, 2, 3) that obeys the Hamiltonian described in equation (4), which includes comparable DM, single-ion axial anisotropy and magnetic exchange interactions.
Collectively, the neutron diffraction and RIXS measurements on Cd2Os2O7 have provided a unique and direct probe of the 5d electrons responsible for the concurrent magnetic order and MIT in both the metallic and insulating regimes, and accessed the role of SOC. The results revealed a mechanism of strong CEF (10Dq≈4.5 eV), moderate Hunds coupling (JH≈0.3 eV) and reduced effective SOC in the creation of the electronic ground state. While the SOC does not appreciably influence the electronic ground state manifold, it enhances the anisotropic magnetic couplings to create an AIAO magnetic ground state and the magnetic excitation out of this ground state at the MIT that corresponds to a superposition of multiple spin-flip processes. This reveals a non-trivial and variable role of effective SOC in 5d3-based systems compared to 5d5 systems, such as the Ir4+ iridates, where SOC plays a more consistently dominant role. The behaviour in Cd2Os2O7 suggests that in general a route beyond the Mott–Hubbard paradigm is required to open the insulating gap in 5d pyrochlores, with AIAO magnetism the likely driving mechanism.
Methods
NPD measurements
NPD measurements were performed on the HB-2A powder diffractometer at the High Flux Isotope Reactor (HFIR), Oak Ridge National Laboratory28. Isotopic 114Cd2Os2O7 was used to overcome the substantial neutron absorption from elemental cadmium. Measurements were performed using a wavelength of 2.41 Å between 4 and 250 K. The magnetic structure was refined using Fullprof and SARAh29 utilizing an irreducible representational analysis approach. The Γ3 irreducible representation was used for the final solution, after trying all possible irreducible representation solutions for a propagation vector of k=(0,0,0), and finding this to be the only solution that described the data. The solution corresponds to the all-in/all-out magnetic structure for the magnetic Os ion at the (0,0,0) site in the pyrochlore structure. This corresponds to the magnetic space group Fd-3m’ in Belov-Neronova-Smirnova (BNS) notation and standard setting. We obtained the ordered-magnetic moment from the Fullprof refinement by normalizing the magnetic scattering to the nuclear reflections and further checked the lower and upper error bounds were an accurate reflection of the data.
Resonant inelastic X-ray scattering
Single crystals of Cd2Os2O7 were measured with RIXS at the Os L3-edge (10.88 KeV) on Sector 30 at the Advanced Photon Source (APS) using the MERIX instrumentation30. The incident energy was accessed with two pre-sample monochromators, a primary diamond(111) monochromator and a secondary Si(400) monochromator. The energy of the beam scattered from the sample was discriminated with a Si(466) 2m diced analyzer. The detector was a MYTHEN strip detector. To reduce the elastic line, we performed inelastic measurements in horizontal geometry within a few degrees of 90°. The RIXS energy resolution was 130 meV FWHM. This is comparable to initial RIXS measurements on iridates that resolved both the SOC splitting of the t2g bands into jeff=1/2 and jeff=3/2 shells, and dispersive magnetic excitations16. The Cd2Os2O7 single crystal was oriented in the (HKK) scattering plane to access high-symmetry directions in the Brillouin zone. Measurements were performed in the same Brillouin zone, and all measurements were performed more than once. The fitting described in the text was on the basis of a least squares analysis. For the dispersion relation in Fig. 3e nominal error of 50 meV has been reported, that is larger than the error obtained by least squares, to account for the variation of the elastic line.
Full exact diagonalisation calculations
The ground state and all possible excited states of the Hamiltonian (equation (4)) with unitary vectors  and
and  were obtained for given 8-site and 4-site clusters with a parameter set reported in ref. 24. Using the states we calculated the excitation spectrum I(ω)=Sn|<yn|Ô| y0>|2d(ω−En+E0), where En are the n-th eigenstate and eigenenergy (n=0 corresponds to the ground state). The applied operator was taken as Ô=S+, (S+)2, (S+)3 for ΔSz=1, 2, 3 excitation channels, respectively. Additional calculations were run on a 4-site cluster, which is the minimum to reproduce the all-in/all-out magnetic structure, to test for finite size effects. The results between the 4-site and 8-site showed very little difference.
were obtained for given 8-site and 4-site clusters with a parameter set reported in ref. 24. Using the states we calculated the excitation spectrum I(ω)=Sn|<yn|Ô| y0>|2d(ω−En+E0), where En are the n-th eigenstate and eigenenergy (n=0 corresponds to the ground state). The applied operator was taken as Ô=S+, (S+)2, (S+)3 for ΔSz=1, 2, 3 excitation channels, respectively. Additional calculations were run on a 4-site cluster, which is the minimum to reproduce the all-in/all-out magnetic structure, to test for finite size effects. The results between the 4-site and 8-site showed very little difference.
Synthesis
Single crystals of Cd2Os2O7 of approximate dimensions 0.2 mm3 were grown as described in ref. 9 by sealing appropriate quantities of CdO, Os and KClO3 in a silica tube and heating at 800 °C for 1 week. Before the RIXS measurement, several crystals were characterized and aligned with an X-ray Laue. All RIXS measurements were performed on a single crystal of Cd2Os2O7. Polycrystalline 114Cd2Os2O7 was prepared with isotopic 114Cd for neutron measurements to negate the extremely high-neutron absorption of standard Cd using solid state techniques from 114CdO and OsO2 powders.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Additional information
How to cite this article: Calder, S. et al. Spin-orbit-driven magnetic structure and excitation in the 5d pyrochlore Cd2Os2O7. Nat. Commun. 7:11651 doi: 10.1038/ncomms11651 (2016).
References
Mott, N. F. Metal-Insulator Transitions Taylor & Francis (1974).
Pesin, D. & Balents, L. Mott physics and band topology in materials with strong spin-orbit interaction. Nat. Phys. 6, 376–381 (2010).
Kim, B. J. et al. Novel Jeff=1/2 Mott state induced by relativistic spin-orbit coupling in Sr2IrO4 . Phys. Rev. Lett. 101, 076402 (2008).
Kim, B. J. et al. Phase-sensitive observation of a spin-orbital mott state in Sr2IrO4 . Science 323, 1329–1332 (2009).
Wan, X., Turner, A. M., Vishwanath, A. & Savrasov, S. Y. Topological semimetal and Fermi-arc surface states in the electronic structure of pyrochlore iridates. Phys. Rev. B 83, 205101 (2011).
Witczak-Krempa, W., Chen, G., Kim, Y. B. & Balents, L. Correlated quantum phenomena in the strong spin-orbit regime. Annu. Rev. Conden. Matter Phys. 5, 57–82 (2014).
Shinaoka, H., Miyake, T. & Ishibashi, S. Noncollinear magnetism and spin-orbit coupling in 5d pyrochlore oxide Cd2Os2O7 . Phys. Rev. Lett. 108, 247204 (2012).
Yamaura, J. et al. Tetrahedral magnetic order and the metal-insulator transition in the pyrochlore lattice of Cd2Os2O7 . Phys. Rev. Lett. 108, 247205 (2012).
Mandrus, D. et al. Continuous metal-insulator transition in the pyrochlore Cd2Os2O7 . Phys. Rev. B 63, 195104 (2001).
Padilla, W. J., Mandrus, D. & Basov, D. N. Searching for the Slater transition in the pyrochlore Cd2Os2O7 with infrared spectroscopy. Phys. Rev. B 66, 035120 (2002).
Matsuda, Y. H. et al. Orbital magnetism in Cd2Os2O7 studied by X-ray magnetic circular dichroism. Phys. Rev. B 84, 174431 (2011).
Slater, J. C. Magnetic effects and the Hartree–Fock Equation. Phys. Rev 82, 538–541 (1951).
Lefrançois, E. et al. Anisotropy-tuned magnetic order in pyrochlore iridates. Phys. Rev. Lett. 114, 247202 (2015).
Sagayama, H. et al. Determination of long-range all-in-all-out ordering of Ir4+ moments in a pyrochlore iridate Eu2Ir2O7 by resonant X-ray diffraction. Phys. Rev. B 87, 100403 (R) (2013).
Ueda, K. et al. Magnetic field-induced insulator-semimetal transition in a pyrochlore Nd2Ir2O7 . Phys. Rev. Lett. 115, 056402 (2015).
Kim, J. et al. Magnetic excitation spectra of Sr2IrO4 probed by resonant inelastic X-ray scattering: establishing links to cuprate superconductors. Phys. Rev. Lett. 108, 177003 (2012).
Kim, J. et al. Large spin-wave energy gap in the bilayer iridate Sr3Ir2O7: evidence for enhanced dipolar interactions near the mott metal-insulator transition. Phys. Rev. Lett. 109, 157402 (2012).
Sala, M. M. et al. CaIrO3: a spin-orbit mott insulator beyond the jeff=1/2 ground state. Phys. Rev. Lett. 112, 176402 (2014).
Liu, X. et al. Testing the validity of the strong spin-orbit-coupling limit for octahedrally coordinated iridate compounds in a model system Sr3CuIrO6 . Phys. Rev. Lett. 109, 157401 (2012).
Gretarsson, H. et al. Crystal-field splitting and correlation effect on the electronic structure of A2IrO3 . Phys. Rev. Lett. 110, 076402 (2013).
Kim, J. et al. Excitonic quasiparticles in a spin-orbit Mott insulator. Nat. Commun. 5, 4453 (2014).
Hozoi, L. et al. Longer-range lattice anisotropy strongly competing with spin-orbit interactions in pyrochlore iridates. Phys. Rev. B 89, 11511 (2014).
Taylor, A. E. et al. Magnetic order and electronic structure of the 5d3 double perovskite Sr2ScOsO6 . Phys. Rev. B 91, 100406(R) (2015).
Bogdanov, N. A., Maurice, R., Rousochatzakis, I., van den Brink, J. & Hozoi, L. Magnetic state of pyrochlore Cd2Os2O7 emerging from strong competition of ligand distortions and longer-range crystalline anisotropy. Phys. Rev. Lett. 110, 127206 (2013).
Georges, A., Medici, L. D. & Mravlje, J. Strong correlations from Hund’s coupling. Annu. Rev. Condens. Matter Phys. 4, 137–178 (2013).
Abragam, A. & Bleaney, B. Electron Paramagnetic Resonance of Transition Ions Clarendon Press, (1970).
Ament, L. J. P., Veenendaal, M. V., Devereaux, T. P., Hill, J. P. & Brink, J. V. D. Resonant inelastic X-ray scattering studies of elementary excitations. Rev. Mod. Phys 83, 705–767 (2011).
Garlea, V. O. et al. The high-resolution powder diffractometer at the high flux isotope reactor. Appl. Phys. A 99, 531–535 (2010).
Wills, A. S. A new protocol for the determination of magnetic structures using Simulated Annealing and Representational Analysis- SARAh. Physica B 276, 680–681 (2000).
Gog, T. et al. Momentum-resolved resonant and nonresonant inelastic X-ray scattering at the advanced photon source. Synchrotron Radiat. News 22, 12 (2009).
Acknowledgements
We thank D.J. Singh for useful discussions. Work at ORNL’s High Flux Isotope reactor was supported by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy (DOE). Use of the Advanced Photon Source, an Office of Science User Facility operated for the U.S. DOE Office of Science by Argonne National Laboratory, was supported by the U.S. DOE under Contract No. DE-AC02-06CH11357. Work in London was supported by the EPSRC. Work in Dresden was supported by the German Research Foundation (SFB 1143 of the Deutsche Forschungsgemeinschaft). Work performed at Brookhaven National Laboratory was supported by the US DOE under contract no. DE-AC02-98CH10886. X.L. acknowledges financial support from MOST (No. 2015CB921302) and CAS (No: XDB07020200) of China. D.M. and J.-Q.Y. acknowledge support from the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Sciences and Engineering Division. Z.Z. was partially supported by the CEM and NSF MRSEC under Grant No. DMR-1420451.
Author information
Authors and Affiliations
Contributions
S.C. and A.D.C. conceived the investigation. S.C., J.G.V., X.L., C.D., M.H.U., D.C., A.D.C. performed the RIXS experiment, as well as conceiving the experiment along with J.P.H., D.F.M., J.v.d.B. and M.D.L. A.H.S. prepared the analyzer for the RIXS measurements. S.C. performed the neutron diffraction experiment. Z.Z., J-Q.Y. and D.M. prepared the samples. N.B., S.N. and J.v.d.B. performed the theoretical calculations. S.C. led the manuscript preparation and all authors contributed.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Calder, S., Vale, J., Bogdanov, N. et al. Spin-orbit-driven magnetic structure and excitation in the 5d pyrochlore Cd2Os2O7. Nat Commun 7, 11651 (2016). https://doi.org/10.1038/ncomms11651
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms11651
This article is cited by
-
Ferromagnetism above 1000 K in a highly cation-ordered double-perovskite insulator Sr3OsO6
Nature Communications (2019)
-
Coexistence of metallic and nonmetallic properties in the pyrochlore Lu2Rh2O7
npj Quantum Materials (2019)
-
Quartz-based flat-crystal resonant inelastic x-ray scattering spectrometer with sub-10 meV energy resolution
Scientific Reports (2018)
-
Strongly-coupled quantum critical point in an all-in-all-out antiferromagnet
Nature Communications (2018)
-
Two-magnon scattering in the 5d all-in-all-out pyrochlore magnet Cd2Os2O7
Nature Communications (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.