Abstract
Solar coronal mass ejections (CMEs) are the most significant drivers of adverse space weather on Earth, but the physics governing their propagation through the heliosphere is not well understood. Although stereoscopic imaging of CMEs with NASA's Solar Terrestrial Relations Observatory (STEREO) has provided some insight into their three-dimensional (3D) propagation, the mechanisms governing their evolution remain unclear because of difficulties in reconstructing their true 3D structure. In this paper, we use a new elliptical tie-pointing technique to reconstruct a full CME front in 3D, enabling us to quantify its deflected trajectory from high latitudes along the ecliptic, and measure its increasing angular width and propagation from 2 to 46  (∼0.2 AU). Beyond 7
(∼0.2 AU). Beyond 7  , we show that its motion is determined by an aerodynamic drag in the solar wind and, using our reconstruction as input for a 3D magnetohydrodynamic simulation, we determine an accurate arrival time at the Lagrangian L1 point near Earth.
, we show that its motion is determined by an aerodynamic drag in the solar wind and, using our reconstruction as input for a 3D magnetohydrodynamic simulation, we determine an accurate arrival time at the Lagrangian L1 point near Earth.
Similar content being viewed by others
Introduction
Coronal mass ejections (CMEs) are spectacular eruptions of plasma and magnetic field from the surface of the Sun into the heliosphere. Travelling at speeds of up to 2,500 km s−1 and with masses of up to 1016 g, they are recognized as drivers of geomagnetic disturbances and adverse space weather on Earth and on other planets in the solar system1,2. Affecting our magnetosphere with average magnetic field strengths of 13 nT and energies of ∼1025 J, they can cause telecommunication and Global Positioning System (GPS) errors, power grid failures and increased radiation risks to astronauts3. It is therefore important to understand the forces that determine their evolution, in order to better forecast their arrival time and impact on Earth and throughout the heliosphere.
Identifying the specific processes that trigger the eruption of CMEs is the subject of much debate, and many different models exist to explain these4,5,6. One common feature is that magnetic reconnection is responsible for the destabilization of magnetic flux ropes on the Sun, which then erupt through the corona into the solar wind to form CMEs7. In the low solar atmosphere, it is postulated that high-latitude CMEs undergo deflection as they are often observed at different position angles than their associated source region locations8. It has been suggested that field lines from polar coronal holes may guide high-latitude CMEs towards the equator9, or that the initial magnetic polarity of a flux rope relative to the background magnetic field influences its trajectory10,11. During this early phase, CMEs are observed to expand outwards from their launch site, although plane-of-sky measurements of their increasing sizes and angular widths are ambiguous in this regard12. This expansion has been modelled as being due to a pressure gradient between the flux rope and the background solar wind13,14. At larger distances in their propagation, CMEs are expected to interact with the solar wind and the interplanetary magnetic field. Studies that compare in situ CME velocity measurements with initial eruption speeds through the corona show that slow CMEs are accelerated towards the speed of the solar wind, and fast CMEs decelerated15,16. It has been suggested that this is due to the effects of drag on the CME in the solar wind17,18. However, the quantification of drag, along with that of both CME expansion and non-radial motion, is currently lacking, primarily because of the limits of observations from single fixed viewpoints with restricted fields of view. The projected two-dimensional nature of these images introduces uncertainties in kinematical and morphological analyses, and therefore the true three-dimensional (3D) geometry and dynamics of CMEs have been difficult to resolve. Efforts were made to infer 3D structure from two-dimensional images recorded by the large angle spectrometric coronagraph on board the Solar and Heliospheric Observatory, situated at the first Lagrangian point (L1), at which its orbital motion around the Sun is synchronous with that of the Earth's. These efforts were based on either a preassumed geometry of the CME19,20,21 or a comparison of observations with in situ and on-disk data22,23. Of note is the polarization technique used to reconstruct the 3D geometry of CMEs in large angle spectrometric coronagraph data24, although this is only valid for heights of up to 5  (1
(1  ).
).
Recently, new methods to track CMEs in 3D have been developed for the Solar Terrestrial Relations Observatory (STEREO) mission25. Launched by NASA in 2006, STEREO consists of two near-identical spacecrafts in heliocentric orbits ahead and behind the Earth, which drift away from the Sun–Earth line at a rate of ± 22° per year. This provides a unique twin perspective of the Sun and inner heliosphere, and enables the implementation of a variety of methods for studying CMEs in 3D26. Many of these techniques are applied within the context of an epipolar geometry27. One such technique consists of tie-pointing lines of sight across epipolar planes, and is best for resolving a single feature such as a coronal loop on-disk28. Under the assumption that the same feature may be tracked in coronagraph images, many CME studies have also used tie-pointing techniques with the COR1 and COR2 coronagraphs of the Sun-Earth Connection Coronal and Heliospheric Investigation (SECCHI29) aboard STEREO30,31,32. The additional use of SECCHI's Heliospheric Imagers (HI1/2) allows a study of CMEs out to distances of 1 astronomical unit (1 AU=149.6×106 km); however, a 3D analysis can only be carried out if the CME propagates along a trajectory between the two spacecrafts so that it is observed by both HI instruments. Otherwise, assumptions of its trajectory have to be inferred from either its association with a source region on-disk33 or its trajectory through the COR data15, or derived by assuming a constant velocity through the HI fields of view34. Triangulation of CME features using time-stacked intensity slices at a fixed latitude, named 'J-maps' because of the characteristic propagation signature of a CME, has also been developed35,36. This technique is hindered by the same limitation of standard tie-pointing techniques, namely, that the curvature of the feature is not considered, and the intersection of sight lines may not occur on the surface of the observed feature. Alternatively, forward modelling of a 3D flux rope based on a graduated cylinder model may be applied to STEREO observations37. Some of the parameters governing the model shape and orientation may be changed by the user to best fit the twin observations simultaneously, although the assumed flux rope geometry is not always appropriate. We have developed a new 3D triangulation technique that overcomes the limitations of previous methods by considering the curvature of the CME front in the data. This functions as a necessary third constraint on the reconstruction of the CME front from the combined observations of the twin STEREO spacecraft. Applying this to every image in the sequence enables us to investigate the changing dynamics and morphology of the CME as it propagates from the Sun into interplanetary space.
Results
CME observation
On 12 December 2008, an erupting prominence was observed by STEREO while the spacecraft was in near quadrature at 86.7° separation (Fig. 1a). The eruption were visible at 50–55° north from 03:00 UT in SECCHI/Extreme Ultraviolet Imager (EUVI) images, obtained in the 304 Å passband, in the northeast from the perspective of STEREO-(A)head and off the northwest limb from STEREO-(B)ehind. The prominence is considered to be the inner material of the CME, which was first observed in COR1-B at 05:35 UT (Fig. 1b). For our analysis, we use the two coronagraphs (COR1/2) and the inner HI1 (Fig. 1c). We characterize the propagation of the CME across the plane of sky by fitting an ellipse to the front of the CME in each image38 (Supplementary Movie 1). This ellipse fitting is applied to the leading edges of the CME but equal weight is given to the CME flank edges as they enter the field of view of each instrument. The 3D reconstruction is then performed using a method of elliptical tie pointing within epipolar planes containing the two STEREO spacecraft, illustrated in Figure 2 (see Methods section).
(a) Indicates the STEREO spacecraft locations, separated by an angle of 86.7° at the time of the event. (b) Shows the prominence eruption observed in EUVI-B off the northwest limb from approximately 03:00 UT, which is considered to be the inner material of the CME. The multiscale edge detection and corresponding ellipse characterization are overplotted in COR1. (c) Shows that the CME is Earth-directed, being observed off the east limb in STEREO-A and off the west limb in STEREO-B.
The reconstruction is performed using an elliptical tie-pointing technique within epipolar planes containing the two STEREO spacecraft27. For example, one of any number of planes will intersect the ellipse characterization of the CME at two points in each image from STEREO-A and B. (a) Illustrates how the resulting four sight lines intersect in 3D space to define a quadrilateral that constrains the CME front in that plane56,57. Inscribing an ellipse within the quadrilateral such that it is tangent to each sight line58,59 provides a slice through the CME that matches the observations from each spacecraft. (b) Illustrates how a full reconstruction is achieved by stacking multiple ellipses from the epipolar slices. As the positions and curvatures of these inscribed ellipses are constrained by the characterized curvature of the CME fronts in the stereoscopic image pair, the modelled CME front is considered to be an optimum reconstruction of the true CME front. (c) Illustrates how this is repeated for every frame of the eruption to build the reconstruction as a function of time and view the changes to the CME front as it propagates in 3D. Although the ellipse characterization applies to both the leading edges and, when observable, the flanks of the CME, only the outermost part of the reconstructed front is shown here for clarity, and illustrated in Supplementary Movie 2.
Non-radial CME motion
It is immediately evident from the reconstruction in Figure 2c (and Supplementary Movie 2) that the CME propagates non-radially away from the Sun. The CME flanks change from an initial latitude span of 16–46° to finally span approximately ± 30° of the ecliptic (Fig. 3b). The mean declination, θ, of the CME is well fitted by a power law of the form  as a result of this non-radial propagation. Tie pointing the prominence apex and fitting a power law to its declination angle result in
as a result of this non-radial propagation. Tie pointing the prominence apex and fitting a power law to its declination angle result in  , implying a source latitude of
, implying a source latitude of  in agreement with EUVI observations. Previous statistics on CME position angles have shown that, during solar minimum, they tend to be offset closer to the equator as compared with those of the associated prominence eruption39. The non-radial motion we quantify here may be evidence of the drawn-out magnetic dipole field of the Sun, an effect predicted at solar minimum because of the influence of solar wind pressure40,41. Other possible influences include changes to the internal current of the magnetic flux rope11, or the orientation of the magnetic flux rope with respect to the background field10, whereby magnetic pressure can function asymmetrically to deflect the flux rope poleward or equatorward depending on the field configurations.
in agreement with EUVI observations. Previous statistics on CME position angles have shown that, during solar minimum, they tend to be offset closer to the equator as compared with those of the associated prominence eruption39. The non-radial motion we quantify here may be evidence of the drawn-out magnetic dipole field of the Sun, an effect predicted at solar minimum because of the influence of solar wind pressure40,41. Other possible influences include changes to the internal current of the magnetic flux rope11, or the orientation of the magnetic flux rope with respect to the background field10, whereby magnetic pressure can function asymmetrically to deflect the flux rope poleward or equatorward depending on the field configurations.
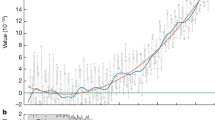
(a) Shows the velocity of the middle of the CME front with the corresponding drag model and, inset, the early acceleration peak. Measurement uncertainties are indicated by one standard deviation error bars. (b) Shows the declinations from the ecliptic (0°) of an angular spread across the front between the CME flanks, with a power-law fit indicative of non-radial propagation. It should be noted that the positions of the flanks are subject to large scatter: as the CME enters each field of view, the location of a tangent to its flanks is prone to moving back along the reconstruction in cases in which the epipolar slices completely constrain the flanks. Hence the 'Midtop/Midbottom of Front' measurements better convey the southward-dominated expansion. (c) Shows the angular width of the CME with a power-law expansion. For each instrument, the first three points of angular width measurement were removed as the CME was still predominantly obscured by each instrument's occulter.
CME angular width expansion
Over the height range of 2–46  , the CME angular width (Δθ=θmax−θmin) increases from ∼30° to ∼60° with a power law of the form
, the CME angular width (Δθ=θmax−θmin) increases from ∼30° to ∼60° with a power law of the form  (Fig. 3c). This angular expansion is evidence of an initial overpressure of the CME relative to the surrounding corona (coincident with its early acceleration inset in Fig. 3a). The expansion then tends to a constant during the later drag phase of CME propagation, as it expands to maintain pressure balance with heliocentric distance. It is theorized that the expansion may be attributed to two types of kinematic evolution, namely, spherical expansion due to simple convection with the ambient solar wind in a diverging geometry, and expansion due to a pressure gradient between the flux rope and solar wind13. It is also noted that the southern portions of the CME manifest the bulk of this expansion below the ecliptic (best observed by comparing the relatively constant 'Midtop of Front' measurements with the more consistently decreasing 'Midbottom of Front' measurements in Fig. 3b). Inspection of a Wang-Sheeley-Arge solar wind model run42 reveals higher speed solar wind flows (∼650 km s−1) emanating from open-field regions at high/low latitudes (approximately 30° north/south of the solar equator). Once the initial prominence/CME eruption occurs and is deflected into a non-radial trajectory, it undergoes asymmetric expansion in the solar wind. It is prevented from expanding upwards into the open-field high-speed stream at higher latitudes, and the high internal pressure of the CME relative to the slower solar wind near the ecliptic accounts for its expansion predominantly to the south. In addition, the northern portions of the CME attain greater distances from the Sun than the southern portions as a result of this propagation in varying solar wind speeds, an effect predicted to occur in previous hydrodynamic models14.
(Fig. 3c). This angular expansion is evidence of an initial overpressure of the CME relative to the surrounding corona (coincident with its early acceleration inset in Fig. 3a). The expansion then tends to a constant during the later drag phase of CME propagation, as it expands to maintain pressure balance with heliocentric distance. It is theorized that the expansion may be attributed to two types of kinematic evolution, namely, spherical expansion due to simple convection with the ambient solar wind in a diverging geometry, and expansion due to a pressure gradient between the flux rope and solar wind13. It is also noted that the southern portions of the CME manifest the bulk of this expansion below the ecliptic (best observed by comparing the relatively constant 'Midtop of Front' measurements with the more consistently decreasing 'Midbottom of Front' measurements in Fig. 3b). Inspection of a Wang-Sheeley-Arge solar wind model run42 reveals higher speed solar wind flows (∼650 km s−1) emanating from open-field regions at high/low latitudes (approximately 30° north/south of the solar equator). Once the initial prominence/CME eruption occurs and is deflected into a non-radial trajectory, it undergoes asymmetric expansion in the solar wind. It is prevented from expanding upwards into the open-field high-speed stream at higher latitudes, and the high internal pressure of the CME relative to the slower solar wind near the ecliptic accounts for its expansion predominantly to the south. In addition, the northern portions of the CME attain greater distances from the Sun than the southern portions as a result of this propagation in varying solar wind speeds, an effect predicted to occur in previous hydrodynamic models14.
CME drag in the inner heliosphere
Investigating the midpoint kinematics of the CME front, we find that the velocity profile increases from approximately 100 to 300 km s−1 over the first 2–5  , before rising more gradually to a scatter between 400 and 550 km s−1 as it propagates outwards (Fig. 3a). The acceleration peaks at approximately 100 m s−2 at a height of ∼3
, before rising more gradually to a scatter between 400 and 550 km s−1 as it propagates outwards (Fig. 3a). The acceleration peaks at approximately 100 m s−2 at a height of ∼3  , then decreases to scatter about zero. This early phase is generally attributed to the Lorentz force whereby the dominant outward magnetic pressure overcomes the internal and/or external magnetic field tension. The subsequent increase in velocity, at heights above ∼7
, then decreases to scatter about zero. This early phase is generally attributed to the Lorentz force whereby the dominant outward magnetic pressure overcomes the internal and/or external magnetic field tension. The subsequent increase in velocity, at heights above ∼7  for this event, is predicted by theory to result from the effects of drag17, as the CME is influenced by solar wind flows of ∼550 km s−1 emanating from latitudes ≳ ± 5° of the ecliptic (again from inspection of the Wang-Sheeley-Arge model). At large distances from the Sun, during this postulated drag-dominated epoch of CME propagation, the equation of motion can be cast in the following form:
for this event, is predicted by theory to result from the effects of drag17, as the CME is influenced by solar wind flows of ∼550 km s−1 emanating from latitudes ≳ ± 5° of the ecliptic (again from inspection of the Wang-Sheeley-Arge model). At large distances from the Sun, during this postulated drag-dominated epoch of CME propagation, the equation of motion can be cast in the following form:

This describes a CME of velocity vcme, mass Mcme and cross-sectional area Acme propagating through a solar wind flow of velocity vsw and density ρsw. The drag coefficient CD is found to be of the order of unity for typical CME geometries18, whereas the density and area are expected to vary as power-law functions of distance r. Thus, we parameterize the density and geometric variation of the CME and solar wind using a power law43 to obtain

where γ describes the drag regime, which can be either viscous (γ=1) or aerodynamic (γ=2), and α and β are constants primarily related to the cross-sectional area of the CME and the density ratio of the solar wind flow to the CME (ρsw/ρcme). The solar wind velocity is estimated from an empirical model44. We determine a theoretical estimate of the CME velocity as a function of distance by numerically integrating Equation (2) using a fourth order Runge–Kutta scheme and fitting the result to the observed velocities from ∼7 to 46  . The initial CME height, CME velocity, asymptotic solar wind speed and α, β and γ are obtained from a bootstrapping procedure that provides a final best fit to the observations and confidence intervals of the parameters (see Methods section). Best-fit values for α and β were found to be (
. The initial CME height, CME velocity, asymptotic solar wind speed and α, β and γ are obtained from a bootstrapping procedure that provides a final best fit to the observations and confidence intervals of the parameters (see Methods section). Best-fit values for α and β were found to be ( )×10−5 and
)×10−5 and  , which agree with values found in previous modelling work44. The best-fit value for the exponent of the velocity difference between CME and the solar wind, γ, was found to be
, which agree with values found in previous modelling work44. The best-fit value for the exponent of the velocity difference between CME and the solar wind, γ, was found to be  , which is clear evidence that aerodynamic drag (γ=2) functions during the propagation of the CME in interplanetary space.
, which is clear evidence that aerodynamic drag (γ=2) functions during the propagation of the CME in interplanetary space.
The drag model provides an asymptotic CME velocity of  km s−1 when extrapolated to 1 AU, which predicts the CME to arrive ∼1 day before the Advanced Composition Explorer (ACE) or WIND spacecraft detects it at the L1 point. We investigate this discrepancy by using our 3D reconstruction to simulate the continued propagation of the CME from the Alfvén radius (∼21.5
km s−1 when extrapolated to 1 AU, which predicts the CME to arrive ∼1 day before the Advanced Composition Explorer (ACE) or WIND spacecraft detects it at the L1 point. We investigate this discrepancy by using our 3D reconstruction to simulate the continued propagation of the CME from the Alfvén radius (∼21.5  ) to Earth using the ENLIL with Cone Model21 at NASA's Community Coordinated Modeling Center. ENLIL is a time-dependent 3D magnetohydrodynamic code that models CME propagation through interplanetary space. We use the height, velocity and width from our 3D reconstruction as initial conditions for the simulation, and find that the CME is actually slowed to ∼342 km s−1 at 1 AU. This is a result of its interaction with an upstream, slow-speed, solar wind flow at distances beyond 50
) to Earth using the ENLIL with Cone Model21 at NASA's Community Coordinated Modeling Center. ENLIL is a time-dependent 3D magnetohydrodynamic code that models CME propagation through interplanetary space. We use the height, velocity and width from our 3D reconstruction as initial conditions for the simulation, and find that the CME is actually slowed to ∼342 km s−1 at 1 AU. This is a result of its interaction with an upstream, slow-speed, solar wind flow at distances beyond 50  . This CME velocity is consistent with in situ measurements of solar wind speed (∼330 km s−1) from the ACE and WIND spacecraft at L1. Tracking the peak density of the CME front from the ENLIL simulation gives an arrival time at L1 of ∼08:09 UT on 16 December 2008. Accounting for the offset in CME front heights between our 3D reconstruction and ENLIL simulation at distances of 21.5
. This CME velocity is consistent with in situ measurements of solar wind speed (∼330 km s−1) from the ACE and WIND spacecraft at L1. Tracking the peak density of the CME front from the ENLIL simulation gives an arrival time at L1 of ∼08:09 UT on 16 December 2008. Accounting for the offset in CME front heights between our 3D reconstruction and ENLIL simulation at distances of 21.5  gives an arrival time in the range of 08:09–13:20 UT on 16 December 2008. This prediction interval agrees well with the earliest derived arrival times of the CME front plasma pileup ahead of the magnetic cloud flux rope from the in situ data of both ACE and WIND (Fig. 4) before its subsequent impact on Earth34,36.
gives an arrival time in the range of 08:09–13:20 UT on 16 December 2008. This prediction interval agrees well with the earliest derived arrival times of the CME front plasma pileup ahead of the magnetic cloud flux rope from the in situ data of both ACE and WIND (Fig. 4) before its subsequent impact on Earth34,36.
From top to bottom, the panels show proton density, bulk flow speed, proton temperature and magnetic field strength and components. The red dashed lines indicate the predicted window of CME arrival time from our ENLIL with Cone Model run (08:09–13:20 UT on 16 December 2008). We observed a magnetic cloud flux rope signature behind the front, highlighted by the blue dash-dotted lines.
Discussion
Since its launch, the dynamic twin viewpoints of STEREO have enabled studies of the true propagation of CMEs in 3D space. Our new elliptical tie-pointing technique uses the curvature of the CME front as a necessary third constraint on the two viewpoints to build an optimum 3D reconstruction of the front. Here, the technique is applied to an Earth-directed CME, to reveal numerous forces that take effect throughout its propagation.
The early acceleration phase results from the rapid release of energy when the CME dynamics are dominated by outward magnetic and gas pressure forces. Different models can reproduce the early acceleration profiles of CME observations, although it is difficult to distinguish between them with absolute certainty45,46. For this event, the acceleration phase coincides with a strong angular expansion of the CME in the low corona, which tends towards a constant in the later observed propagation in the solar wind. Although, statistically, expansion of CMEs is a common occurrence47, it is difficult to accurately determine the magnitude and rate of expansion across the two-dimensional plane-of-sky images for individual events. Some studies of these single-viewpoint images of CMEs use characterizations such as the cone model20,21 but assume the angular width to be constant (rigid cone), which is not always true early in the events12,38. Our 3D front reconstruction overcomes the difficulties in distinguishing expansion from image projection effects, and we show that early in this event there is a non-constant, power-law, angular expansion of the CME. Theoretical models of CME expansion generally reproduce constant radial expansion, based on the suspected magnetic and gas pressure gradients between the erupting flux rope and the ambient corona and solar wind14,48,49. To account for the angular expansion of the CME, a combination of internal overpressure relative to external gas and magnetic pressure dropoffs, along with convective evolution of the CME in the diverging solar wind geometry, must be considered13.
During this early-phase evolution, the CME is deflected from a high-latitude source region into a non-radial trajectory, as indicated by the changing inclination angle (Fig. 3b). Although projection effects again hinder interpretations of CME position angles in single images, statistical studies show that, relative to their source region locations, CMEs have a tendency to deflect towards lower latitudes during solar minimum39,50. It has been suggested that this results from the guiding of CMEs towards the equator by either the magnetic fields emanating from polar coronal holes8,9 or the flow pattern of the background coronal magnetic field and solar wind/streamer influences19,51. Other models show that the internal configuration of the erupting flux rope can have an important effect on its propagation through the corona. The orientation of the flux rope, either normal or inverse polarity, will determine where magnetic reconnection is more likely to occur, and therefore change the magnetic configuration of the system to guide the CME either equator- or poleward10. Alternatively, modelling the filament as a toroidal flux rope located above a midlatitude polarity inversion line results in non-radial motion and acceleration of the filament, because of the guiding action of the coronal magnetic field on the current motion11. Both these models have a dependence on the chosen background magnetic field configuration, and so the suspected drawn-out magnetic dipole field of the Sun by the solar wind40,41 may be the dominant factor in deflecting the prominence/CME eruption into this observed non-radial trajectory.
At larger distances from the Sun (>7  ), the effects of drag become important as the CME velocity approaches that of the solar wind. The interaction between the moving magnetic flux rope and the ambient solar wind has been suggested to have a key role in CME propagation at large distances at which the Lorentz driving force and the effects of gravity become negligible4. Comparisons of initial CME speeds and in situ detections of arrival times have shown that velocities converge on the solar wind speed15,16. For this event, we find that the drag force is indeed sufficient to accelerate the CME to the solar wind speed, and quantify that the kinematics are consistent with the quadratic regime of aerodynamic drag (turbulent, as opposed to viscous, effects dominate). The importance of drag becomes further apparent through the CME interaction with a slow-speed solar wind stream ahead of it, slowing it to a speed that accounts for the observed arrival time at L1 near Earth. This agrees with the conjecture that Sun–Earth transit time is more closely related to the solar wind speed than the initial CME speed52. Other kinematic studies of this CME through the HI fields of view quote velocities of 411 ± 23 km s−1 (Ahead) and 417 ± 15 km s−1 (Behind) when assumed to have zero acceleration during this late phase of propagation34, or an average of 363 ± 43 km s−1 when triangulated in time-elongation J-maps36. These speeds through the HI fields of view, lower than those quantified through the COR1/2 fields of view, agree somewhat with the deceleration of the CME to match the slow-speed solar wind ahead of it in our magnetohydrodynamic simulation. Ultimately, we are able to predict a more accurate arrival time of the CME front at L1.
), the effects of drag become important as the CME velocity approaches that of the solar wind. The interaction between the moving magnetic flux rope and the ambient solar wind has been suggested to have a key role in CME propagation at large distances at which the Lorentz driving force and the effects of gravity become negligible4. Comparisons of initial CME speeds and in situ detections of arrival times have shown that velocities converge on the solar wind speed15,16. For this event, we find that the drag force is indeed sufficient to accelerate the CME to the solar wind speed, and quantify that the kinematics are consistent with the quadratic regime of aerodynamic drag (turbulent, as opposed to viscous, effects dominate). The importance of drag becomes further apparent through the CME interaction with a slow-speed solar wind stream ahead of it, slowing it to a speed that accounts for the observed arrival time at L1 near Earth. This agrees with the conjecture that Sun–Earth transit time is more closely related to the solar wind speed than the initial CME speed52. Other kinematic studies of this CME through the HI fields of view quote velocities of 411 ± 23 km s−1 (Ahead) and 417 ± 15 km s−1 (Behind) when assumed to have zero acceleration during this late phase of propagation34, or an average of 363 ± 43 km s−1 when triangulated in time-elongation J-maps36. These speeds through the HI fields of view, lower than those quantified through the COR1/2 fields of view, agree somewhat with the deceleration of the CME to match the slow-speed solar wind ahead of it in our magnetohydrodynamic simulation. Ultimately, we are able to predict a more accurate arrival time of the CME front at L1.
A cohesive physical picture for how the CME erupts, propagates and expands in the solar atmosphere remains to be fully developed and understood from a theoretical perspective. Realistic magnetohydrodynamic models of the Sun's global magnetic field and solar wind are required to explain all processes that take effect, along with a need for adequate models of the complex flux rope geometries within CMEs. In addition, ambitious space exploration missions, such as Solar Orbiter53 (ESA) and Solar Probe+54 (NASA), will be required to give us a better understanding of the fundamental plasma processes responsible for driving CMEs and determining their adverse effects on Earth.
Methods
CME front detection and characterization
For the coronagraph images of COR1/2, a multiscale filter was used to determine a scale at which the signal-to-noise ratio of the CME was deemed optimal for the pixel-chaining algorithm to highlight the edges in the images55. To specifically determine the CME front, running and fixed difference masks were overlaid on the multiscale edge detections of both the Ahead and Behind viewpoints simultaneously, enabling us to confidently point and click along the relevant CME front edges in each image. For the Heliospheric images of HI1, a modified running difference was used to enhance the faint CME features by correcting for the apparent background stellar motion between frames15. The CME was scaled to an appropriate level for pointing and clicking along its front. Once the CME fronts were determined across each instrument plane of sky, an ellipse was fit to each front to characterize the changing morphology of the CME38.
Elliptical tie pointing
Three-dimensional information may be gleaned from two independent viewpoints of a feature using tie-pointing techniques to triangulate lines of sight in space27. However, when the object is known to be a curved surface, sight lines will be tangent to it and not necessarily intersect upon it. Consequently, CMEs cannot be reconstructed by tie pointing alone, but rather their localization may be constrained by intersecting sight lines tangent to the leading edges of a CME56,57. It is possible to extract the intersection of a given epipolar plane through the ellipse fits in both the Ahead and Behind images, resulting in a quadrilateral in 3D space. Inscribing an ellipse within the quadrilateral, such that it is tangent to all four sides58,59, provides a slice through the CME that matches the observations from each spacecraft. A full reconstruction is achieved by stacking ellipses from numerous epipolar slices. As the positions and curvatures of these inscribed ellipses are constrained by the characterized curvature of the CME front in the stereoscopic image pair, the modelled CME front is considered as an optimum reconstruction of the true CME front. This is repeated for every frame of the eruption to build the reconstruction as a function of time and view the changes to the CME front as it propagates in 3D.
Following Horwitz59, we inscribe an ellipse within a quadrilateral using the following steps (see Fig. 5):
• Apply an isometry to the plane such that the quadrilateral has vertices (0, 0), (A, B), (0, C), (s, t), where, in the case of an affine transformation, we set A=1, B=0 and C=1, with s and t as variables.
• Set the ellipse centre point (h, k) by fixing h somewhere along the open line segment connecting the midpoints of the diagonals of the quadrilateral and hence determine k from the equation of a line, for example

• To solve for the ellipse tangent to the four sides of the quadrilateral, we can solve for the ellipse tangent to the three sides of a triangle the vertices of which are the complex points

and the two ellipse foci are then the zeroes of the equation

the discriminant of which can be denoted by r (h)=r1 (h)+ir2 (h) where


Thus, we need to determine the quartic polynomial u (h)=|r (h)|2=r1 (h)2+r2 (h)2 and we can then solve for the ellipse semimajor axis a and semiminor axis b from the equations


by parameterizing R=a2−b2 and W=a2b2 to obtain

• Knowing the axes, we can generate the ellipse and float its tilt angle δ until it sits tangent to each side of the quadrilateral, using the inclined ellipse equation

where ω′=ω+δ and ω is the angle from the semimajor axis to a radial line ρ on the ellipse.
Drag modelling
The evolution of CMEs as they propagate from the Sun through the heliosphere is a complex process, simplified by using a parameterized drag model. Comparing Equation (1) and Equation (2)

where CD and Mcme are approximately constant, and Acme and ρsw are functions of distance expected to have a power-law form. We can therefore represent their combined behaviour as a single power law, as in Equation (12). For example, if we assume a density profile of ρsw (r)=ρ0r−2, and a cylindrical CME of area Acme (r)=A0r, then from Equation (12) we expect β=1. The α parameter, representative of the strength of the interaction, is then determined by the constants A0, Mcme and CD, such that high-mass, small-volume CMEs are less affected by drag than are low-mass, large-volume CMEs. This method of parameterization has been shown to reproduce the kinematic profiles of a large number of events44. We assume an additional parameter γ to indicate the type of drag, suggested to be either linear (γ=1) or quadratic (γ=2). Although this parameterization may obscure some of the complex interplay between the various quantities, it does not affect the most crucial part that we are trying to test: Is aerodynamic drag an appropriate model and, if so, which regime (linear or quadratic) best characterizes the kinematics?
A bootstrapping technique60 was used to obtain statistically significant parameter ranges from the drag model of Equation (2). This technique involves the following steps:
1. An initial fit to the data y is obtained, yielding the model fit  with parameters
with parameters  .
.
2. The residuals of the fit are calculated:  .
.
3. The residuals are randomly resampled to yield ∈*.
4. The model is then fit to a new data vector y*=y+∈* and the parameters  are stored.
are stored.
5. Steps 3–4 are repeated many times (10,000).
6. Confidence intervals on the parameters are determined from the resulting distributions.
In our case, the model parameters were the initial height hcme of the CME at the start of the modelling; the speed vsw of the solar wind at 1 AU; the velocity vcme of the CME at the start of the modelling; and the drag parameters α, β and γ. To test for self-consistency, we allowed the observationally known parameters of initial CME height and velocity to vary in the bootstrapping procedure, and recovered comparable values. The parameters α and β were in reasonable agreement with values from previous studies44.
Additional information
How to cite this article: Byrne, J.P. et al. Propagation of an Earth-directed coronal mass ejection in three dimensions. Nat. Commun. 1:74 doi: 10.1038/ncomms1077 (2010).
References
Schwenn, R., Dal Lago, A., Huttunen, E. & Gonzalez, W. D. The association of coronal mass ejections with their effects near the Earth. Ann. Geophys. 23, 1033–1059 (2005).
Prangé, R. et al. An interplanetary shock traced by planetary auroral storms from the Sun to Saturn. Nature 432, 78–81 (2004).
Severe Space Weather Events—Understanding Societal and Economic Impacts Workshop Report, National Research Council (National Academies Press, 2008).
Chen, J. Theory of prominence eruption and propagation: interplanetary consequences. J. Geophys. Res. 101, 27499–27520 (1996).
Antiochos, S. K., DeVore, C. R. & Klimchuk, J. A. A model for solar coronal mass ejections. Astrophys. J. 510, 485–493 (1999).
Kliem, B. & Török, T. Torus instability. Phys. Rev. Lett. 96, 255002 (2006).
Moore, R. L. & Sterling, A. C. in Solar Eruptions and Energetic Particles Vol 165 (eds. Gopalswamy, N., Mewaldt, R. & Torsti, J.) 43–57 (American Geophysical Union, 2006).
Xie, H. et al. On the origin, 3D structure and dynamic evolution of CMEs near solar minimum. Sol. Phys. 259, 143–161 (2009).
Kilpua, E. K. J. et al. STEREO observations of interplanetary coronal mass ejections and prominence deflection during solar minimum period. Ann. Geophys. 27, 4491–4503 (2009).
Chané, E., Jacobs, C., van der Holst, B., Poedts, S. & Kimpe, D. On the effect of the initial magnetic polarity and of the background wind on the evolution of CME shocks. Astron. Astrophys. 432, 331–339 (2005).
Filippov, B. P., Gopalswamy, N. & Lozhechkin, A. V. Non-radial motion of eruptive filaments. Sol. Phys. 203, 119–130 (2001).
Gopalswamy, N., Dal Lago, A., Yashiro, S. & Akiyama, S. The expansion and radial speeds of coronal mass ejections. Cen. Eur. Astrophys. Bull. 33, 115–124 (2009).
Riley, P. & Crooker, N. U. Kinematic treatment of coronal mass ejection evolution in the solar wind. Astrophys. J. 600, 1035–1042 (2004).
Odstrčil, D. & Pizzo, V. J. Three-dimensional propagation of coronal mass ejections in a structured solar wind flow 2. CME launched adjacent to the streamer belt. J. Geophys. Res. 104, 493–504 (1999).
Maloney, S. A., Gallagher, P. T. & McAteer, R. T. J. Reconstructing the 3-D trajectories of CMEs in the inner Heliosphere. Sol. Phys. 256, 149–166 (2009).
González-Esparza, J. A., Lara, A., Pérez-Tijerina, E., Santillán, A. & Gopalswamy, N. A numerical study on the acceleration and transit time of coronal mass ejections in the interplanetary medium. J. Geophys. Res. (Space Physics) 108, 1039 (2003).
Tappin, S. J. The deceleration of an interplanetary transient from the Sun to 5 AU. Sol. Phys. 233, 233–248 (2006).
Cargill, P. J. On the aerodynamic drag force acting on interplanetary coronal mass ejections. Sol. Phys. 221, 135–149 (2004).
Cremades, H. & Bothmer, V. On the three-dimensional configurations of coronal mass ejections. Astron. Astrophys. 422, 307–322 (2004).
Zhao, X. P., Plunkett, S. P. & Liu, W. Determination of geometrical and kinematical properties of halo coronal mass ejections using the cone model. J. Geophys. Res. 107, 1223 (2002).
Xie, H., Ofman, L. & Lawrence, G. Cone model for halo CMEs: application to space weather forecasting. J. Geophys. Res. 109, 3109 (2004).
Démoulin, P., Nakwacki, M. S., Dasso, S. & Mandrini, C. H. Expected in situ velocities from a hierarchical model for expanding interplanetary coronal mass ejections. Sol. Phys. 250, 347–374 (2008).
Howard, T. A., Nandy, D. & Koepke, A. C. Kinematics properties of solar coronal mass ejections: correction for projection effects in spacecraft coronagraph measurements. J. Geophys. Res. (Space Physics) 113, 1104 (2008).
Moran, T. G. & Davila, J. M. Three-dimensional polarimetric imaging of coronal mass ejections. Science 305, 66–71 (2004).
Kaiser, M. L. et al. The STEREO mission: an introduction. Space Sci. Rev. 136, 5–16 (2008).
Mierla, M. et al. On the 3-D reconstruction of coronal mass ejections using coronagraph data. Ann. Geophys. 28, 203–215 (2010).
Inhester, B. Stereoscopy basics for the STEREO mission (arXiv: astro-ph/0612649, 2006).
Aschwanden, M. J., Wülser, J. P., Nitta, N. V. & Lemen, J. R. First three-dimensional reconstruction of coronal loops with the STEREO A and B spacecraft. I. Geometry. Astrophys. J. 679, 827–842 (2008).
Howard, R. A. et al. Sun earth connection coronal and heliospheric investigation (SECCHI). Space Sci. Rev. 136, 67–115 (2008).
Liewer, P. C. et al. Stereoscopic analysis of the 19 May 2007 erupting filament. Sol. Phys. 256, 57–72 (2009).
Srivastava, N., Inhester, B., Mierla, M. & Podlipnik, B. 3D reconstruction of the leading edge of the 20 May 2007 partial halo CME. Sol. Phys. 259, 213–225 (2009).
Wood, B. E., Howard, R. A., Thernisien, A., Plunkett, S. P. & Socker, D. G. Reconstructing the 3D morphology of the 17 May 2008 CME. Sol. Phys. 259, 163–178 (2009).
Howard, T. A. & Tappin, S. J. Three-dimensional reconstruction of two solar coronal mass ejections using the STEREO spacecraft. Sol. Phys. 252, 373–383 (2008).
Davis, C. J. et al. Stereoscopic imaging of an Earth-impacting solar coronal mass ejection: a major milestone for the STEREO mission. Geophys. Res. Lett. 36, 8102 (2009).
Davis, C. J., Kennedy, J. & Davies, J. A. Assessing the accuracy of CME speed and trajectory estimates from STEREO observations through a comparison of independent methods. Sol. Phys. 263, 209–222 (2010).
Liu, Y. et al. Geometric triangulations of imaging observations to track coronal mass ejections continuously out to 1 AU. Astrophys. J. Lett. 710, L82–L87 (2010).
Thernisien, A., Vourlidas, A. & Howard, R.A. Forward modeling of coronal mass ejections using STEREO/SECCHI data. Sol. Phys. 256, 111–130 (2009).
Byrne, J. P., Gallagher, P. T., McAteer, R. T. J. & Young, C. A. The kinematics of coronal mass ejections using multiscale methods. Astron. Astrophys. 495, 325–334 (2009).
Gopalswamy, N. et al. Prominence eruptions and coronal mass ejection: a statistical study using microwave observations. Astrophys. J. 586, 562–578 (2003).
Pneuman, G. W. & Kopp, R. A. Gas-magnetic field interactions in the solar corona. Sol. Phys. 18, 258–270 (1971).
Banaszkiewicz, M., Axford, W.T. & McKenzie, J. F. An analytic solar magnetic field model. Astron. Astrophys. 337, 940–944 (1998).
Arge, C. N. & Pizzo, V. J. Improvement in the prediction of solar wind conditions using near-real time solar magnetic field updates. J. Geophys. Res. 105, 10465–10480 (2000).
Vršnak, B. & Gopalswamy, N. Influence of the aerodynamic drag on the motion of interplanetary ejecta. J. Geophys. Res. 107, 1019 (2002).
Vršnak, B. Deceleration of coronal mass ejections. Sol. Phys. 202, 173–189 (2001).
Schrijver, C. J., Elmore, C., Kliem, B., Török, T. & Title, A. M. Observations and modelling of the early acceleration phase of erupting filaments involved in coronal mass ejections. Astrophys. J. 674, 586–595 (2008).
Lin, C.-H., Gallagher, P. T. & Raftery, C. L. Investigating the driving mechanisms of coronal mass ejections. Astron. Astrophys. 516, A44 (2010).
Bothmer, V. & Schwenn, R. Eruptive prominences as sources of magnetic clouds in the solar wind. Space Sci. Rev. 70, 215–220 (1994).
Berdichevsky, D. B., Lepping, R. P. & Farrugia, C. J. Geometric considerations of the evolution of magnetic flux ropes. Phys. Rev. E 67, 036405 (2003).
Cargill, P. J., Schmidt, J., Spicer, D. S. & Zalesak, S. T. Magnetic structure of overexpanding coronal mass ejections: numerical models. J. Geophys. Res. 105, 7509–7520 (2000).
Yashiro, S. et al. A catalog of white light coronal mass ejections observed by the SOHO spacecraft. J. Geophys. Res. (Space Physics) 109, 7105 (2004).
MacQueen, R. M., Hundhausen, A. J. & Conover, C. W. The propagation of coronal mass ejection transients. J. Geophys. Res. 91, 31–38 (1986).
Vršnak, B., Vrbanec, D., Čalogović, J. & Žic, T. The role of aerodynamic drag in dynamics of coronal mass ejections. IAU Symposium 257, 271–277 (2009).
Hassler, D. et al. Solar Orbiter: Exploring the Sun-heliosphere Connection. ESA/SRE(2009)5 (2009).
McComas, D. J. et al. Solar Probe Plus: Report of the Science and Technology Definition Team (STDT). NASA/TM–2008–214161, NASA (2008).
Young, C. A. & Gallagher, P. T. Multiscale edge detection in the corona. Sol. Phys. 248, 457–469 (2008).
Pizzo, V. J. & Biesecker, D. A. Geometric localization of STEREO CMEs. Geophys. Res. Lett. 31, 21802 (2004).
deKoning, C. A., Pizzo, V. J. & Biesecker, D. A. Geometric localization of CMEs in 3D space using STEREO beacon data: first results. Sol. Phys. 256, 167–181 (2009).
Horwitz, A. Finding ellipses and hyperbolas tangent to two, three, or four given lines. Southwest J. Pure Appl. Math. 1, 6–32 (2002).
Horwitz, A. Ellipses of maximal area and of minimal eccentricity inscribed in a convex quadrilateral. Austral. J. Math. Anal. Appl. 2, 1–12 (2005).
Efron, B. & Tibshirani, R. J. An Introduction To The Bootstrap (Chapman & Hall/CRC, 1993).
Acknowledgements
This work is supported by the Science Foundation Ireland under Grants no. 07-RFP-PHYF399 and 729S0DAZ. R.T.J.M.A. was a Marie Curie Fellow at TCD. The STEREO/SECCHI project is an international consortium of the Naval Research Laboratory (USA), Lockheed Martin Solar and Astrophysics Lab (USA), NASA Goddard Space Flight Center (USA), Rutherford Appleton Laboratory (UK), University of Birmingham (UK), Max-Planck-Institut für Sonnen-systemforschung (Germany), Centre Spatial de Liege (Belgium), Institut d'Optique Théorique et Appliquée (France) and Institut d'Astrophysique Spatiale (France). Simulation results have been provided by the Community Coordinated Modeling Center at Goddard Space Flight Center through their public Runs on Request system (http://ccmc.gsfc.nasa.gov). The CCMC is a multiagency partnership between NASA, AFMC, AFOSR, AFRL, AFWA, NOAA, NSF and ONR. The ENLIL with Cone Model was developed by D. Odstrcil at the University of Colorado at Boulder. We acknowledge the use of WIND data.
Author information
Authors and Affiliations
Contributions
J.P.B. developed the method and performed the analysis. S.A.M carried out the drag modelling and bootstrapping procedure and contributed to the analysis. J.M.R. developed the visualization suite. R.T.J.M.A. guided the data prepping. P.T.G. supervised the research. J.P.B., S.A.M., R.T.J.M.A. and P.T.G. discussed the results and implications and contributed to the paper at all stages.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Movie 1
STEREO-Ahead and Behind images of the 12 December 2008 coronal mass ejection. The frames show: the multiscale edge detections on COR1/2 (red lines), and running-difference front detections on HI1 (red points); the ellipse characterisations (blue); and the resulting 3D coronal mass ejection front reconstructions back-projected onto the plane-of-sky (white). The white semi-circles near the centre of each image indicate the limb of the Sun. (MOV 9887 kb)
Supplementary Movie 2
The 3D coronal mass ejection front reconstruction as it propagates along the Sun-Earth line into interplanetary space at distances of 2-46 RSun. The non-radial trajectory and expansion of the coronal mass ejection are very apparent as it propagates away from its high-latitude source region and expands through the ecliptic plane. The relative positions of the STEREO spacecraft and the planets Earth, Mercury and Venus are indicated (as in the schematic of Fig. 1a). (AVI 9668 kb)
Rights and permissions
About this article
Cite this article
Byrne, J., Maloney, S., McAteer, R. et al. Propagation of an Earth-directed coronal mass ejection in three dimensions. Nat Commun 1, 74 (2010). https://doi.org/10.1038/ncomms1077
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/ncomms1077
This article is cited by
-
Rapid Rotation of an Erupting Prominence and the Associated Coronal Mass Ejection on 13 May 2013
Solar Physics (2023)
-
Propagation of coronal mass ejections from the Sun to the Earth
Journal of Astrophysics and Astronomy (2023)
-
Propagation characteristics of coronal mass ejections (CMEs) in the corona and interplanetary space
Reviews of Modern Plasma Physics (2022)
-
Comparing the Heliospheric Cataloging, Analysis, and Techniques Service (HELCATS) Manual and Automatic Catalogues of Coronal Mass Ejections Using Solar Terrestrial Relations Observatory/Heliospheric Imager (STEREO/HI) Data
Solar Physics (2022)
-
Earth-affecting solar transients: a review of progresses in solar cycle 24
Progress in Earth and Planetary Science (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.