Introduction

Understanding how to obtain and measure electron temperatures approaching 1 mK has the potential to open a new regime for studying nanoelectronics and pave the way towards pioneering sub-millikelvin techniques1. This would benefit numerous areas of activity; for example, investigations of the fractional quantum Hall effect in two-dimensional electron gases2,3 and solid-state quantum technologies including superconducting and semiconducting qubits4,5. To access these temperatures one must minimize parasitic heating and internal Joule heating, and maximize the coupling to cold contact wires and phonons in the host lattice, all the while overcoming the decrease in electron–phonon coupling and electrical heat conduction as temperatures drop6.

Here we study Coulomb blockade thermometers (CBTs) that have been designed to operate significantly below 10 mK and demonstrate cooling of electrons in a nanoelectronic device to below 4 mK. A CBT consists of an array of Coulomb-blockaded metallic islands connected by tunnel junctions. The conductance of the array is temperature dependent, due to the balance between thermal excitations and an electrostatic barrier to single electron tunnelling across the islands7,8. CBTs typically function over a decade of temperature and have previously been demonstrated to work at temperatures as low as 7.5 mK (refs 9, 10). Perhaps most importantly, they can be viewed as a primary thermometer of their internal electron temperature. We have used CBTs as a diagnostic tool to quantify and optimize the thermal environment of a nanoelectronic device and to unambiguously determine the local electron temperature. In the future, similar CBTs could be used to probe the electron temperature of nearby samples with thermal contact provided by direct electrical connections. Furthermore, the techniques that are used to cool the CBTs can be used to cool other nanoelectronic samples.

Results

Structure of the thermometer devices

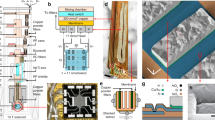
The structure of the CBTs studied here is shown in Fig. 1. Devices are fabricated using an ex situ tunnel junction process11, which provides excellent tunnel junction uniformity12, and has also been used to fabricate superconducting qubits13 (see Methods for details). Efficient thermal coupling between electrons and phonons in the metallic islands of the CBT is critical for reaching low electron temperatures14,15. The electron–phonon heat flow Pep is described by the material-dependent electron–phonon coupling constant Σ and the volume of the metallic island Ω,

Figure 1: Details of the CBT device structure.
figure 1

(a) Optical micrograph of the CBT with equivalent circuit diagram and schematic cross-section of the structure. Scale bar on the optical micrograph, 10 μm. The CBT is formed of 32 × 20 metallic islands of capacitance CΣ connected in an array by tunnel junctions of resistance RT, as shown in the circuit diagram. Connection to the array is made via on-chip RC filters comprising a meandering electrode sandwiched between large-area grounded metal films, separated by 250 nm SiOx. Each filter has a distributed resistance R≈500 Ω and capacitance C≈10 pF. The schematic cross-section shows one Al2O3 tunnel junction connecting two Al islands, with Au thermalization blocks on top of each. (b) Scanning electron microscopic (SEM) image showing Au thermalization blocks. Scale bar, 20 μm. (c) The sidewalls of four adjacent Au blocks. Scale bar, 4 μm. (d) One tunnel junction connecting two adjacent blocks. Scale bar, 1 μm.

Full size image

where Te is the electron temperature and Tp is the phonon temperature16. To minimize Te, the island volume should be large and the material chosen to maximize Σ. We use electroplated Au on top of the CBT islands to increase their volume to nominal 5 × 205 × 38.5 μm3 (see Methods for details). The effective electron–phonon coupling in these islands, with a relatively large volume and a high coupling constant17 in Au Σ=2.4 × 109 WK−5 m−3, is estimated to be more than two orders of magnitude larger than in previous CBTs fabricated using the ex situ junction process18.

In addition to efficient thermalization of the CBT itself, it is important to cool the incoming leads through robust thermal anchoring and heavy electromagnetic filtering19. We improve the chain of thermalization and filtering by including on-chip resistive meander structures in line with all electrical contacts. These form a distributed resistive-capacitive chain with a cutoff frequency ≈40 MHz. Similar filters based on a large area capacitor and tunnel junctions in series have previously been incorporated in a CBT18.

CBT characteristics above 7 mK

Figure 2 shows the behaviour of a CBT fabricated using the process described above, focusing on temperatures between 7 and 80 mK. The sensor is measured in both a commercial cryogen-free dilution refrigerator (Bluefors Cryogenics LD250) with a base temperature ≈7 mK and in a custom dilution refrigerator manufactured at Lancaster University20 with a base temperature ≈2.5 mK. The conductance of the CBT is measured in a current-driven four-wire configuration, with the drive current and voltage amplification provided by an Aivon PA10 amplifier. A small AC excitation (typically 5 pA≤IAC≤100 pA) is added to the DC bias IDC, allowing the differential conductance G to be measured with a lock-in amplifier.

Figure 2: CBT behaviour between 80 and 7 mK in two dilution refrigerators.
figure 2

(a) CBT conductance G versus measured bias voltage VDC at four temperatures. Symbols show measured values and lines show best fits to the calculated ideal conductance. The warmest measurements (crosses, circles and squares) are fitted simultaneously to calibrate the sensor, giving CΣ=236.6 fF and RT=22.42 kΩ. The coldest measurement (triangles) is fitted using this calibration. The minimum electron temperatures are in close agreement with the refrigerator temperature measured by a RuO2 thermometer: 59.9, 40.1, 20.0 and 7.2 mK respectively. The uncertainties on are calculated from uncertainties in the fitted parameters. (b) CBT electron temperature Te versus refrigerator temperature Tmxc. Symbols show from fits to conductance dips measured in the cryogen-free refrigerator (circles) and the custom refrigerator (triangles). Error bars are within the symbols. The solid curve shows Te determined by monitoring the conductance G0 (at VDC=0) as the cryo-free fridge cools over 35 min from 52 to 9 mK, showing that the CBT has a stronger thermal link to the refrigerator than the RuO2 thermometer, leading to the thermal lag (Tmxc≥Te) during this time. The dashed line shows Te=Tmxc.

Full size image

In both refrigerators, the CBT is in a vacuum and housed in a gold-plated copper package (Aivon SH-1) that is attached to the mixing chamber plate. The package includes RC filters with a cutoff frequency ≈300 kHz. Electrical contacts to the CBT are thermalized in additional cold RC filters potted in Eccosorb CR 124 (Aivon Therma), which are also attached to the mixing chamber plate. The filters have a cutoff frequency ≈15 kHz.

As shown in Fig. 2a, the CBT conductance dips around zero bias and the dip becomes deeper and narrower at lower temperatures. Its full-width at half maximum is related to temperature by V1/2≈5.439NkBT/e, where N is the number of tunnel junctions in series7. This result does not account for self-heating in the sensor and so is only applicable when Te=Tp≡T. A more practical parameter to determine temperature is the zero-bias conductance G0, which has an approximate analytic relation to temperature21

where uN≡EC/kBT is the dimensionless inverse temperature, EC≡[(N−1)/N]e2/CΣ is the charging energy of the system, CΣ is the total capacitance of each island and GT is the asymptotic conductance. When uN<2.5, the temperature measurement error is <2.5% (ref. 15). Thus, if CΣ and GT are known, it is possible to determine T by measuring only G0. The most complete method to determine temperature is using a full tunnelling model to calculate G(VDC) numerically7. We use this last approach to find CΣ and GT for the device, and these parameters are then used to find the temperature from subsequent measurements.

Numerical calculations of conductance are made using an algorithm derived from the free, open-source library pyCBT (see Methods for further details). In addition, we account for overheating in the sensor by predicting the electron temperature Te in the islands using a model for the heat flow P into each island,

where the first term is Joule heating at tunnel junctions of resistance RT, the second term is heat flow to phonons and P0 accounts for parasitic heating. For a given phonon temperature, the minimum electron temperature is found at VDC=0. If P0 is small, then .

Figure 2a shows the result of fitting the calculated G(VDC) simultaneously to three measurements made between 20 and 60 mK. The fit parameters are RT, CΣ and TP for each measurement. The fit is found to be insensitive to the value of P0 and hence parasitic heating is assumed to be negligible at these temperatures. Having calibrated the CBT, the fitted CΣ is used to fit further measurements with Tp and RT as the free parameters. An example is given in Fig. 2a, where the electron temperature is found to be 7.2±0.1 mK at a refrigerator temperature of 7.2 mK. Figure 2b shows that the electron temperature measured by the CBT is in close agreement with the refrigerator temperature Tmxc in both refrigerators between 7 and 80 mK. Details of how Tmxc was measured in each fridge can be found in the Methods section.

CBT characteristics below 7 mK

We investigate the behaviour of the CBT below 7 mK in the custom dilution refrigerator. Figure 3a shows the electron temperature of the sensor when in vacuum gradually cooling below 4 mK, while the refrigerator was held at Tmxc≲2.8 mK. Here, Te is determined from the value of G0, which is found by measuring G over a small range of VDC (≈30 μV) close to VDC=0. We observe an extremely long equilibration time (over 3 days) but a rapid cooling of the CBT following a heating event (a refill of the liquid helium bath that briefly heats the CBT above 5.5 mK and the fridge above 3.5 mK). This suggests that the thermal contact between the CBT and the refrigerator is relatively strong, and that its slow cooling is probably due to heat leak from an external warm object.

Figure 3: Thermalization of two CBTs at a refrigerator temperature ≤2.8 mK.
figure 3

(a) Cooling of one CBT in vacuum (circles) and one immersed in the 3He/4He refrigerant of the dilution refrigerator (triangles). In both cases, the CBTs are cooling after being warmed above 10 mK by temporarily increasing the refrigerant temperature. The CBT in vacuum is extremely slow to thermalize. By comparison, the CBT immersed in 3He/4He thermalizes significantly faster. (b) Cooling of the immersed CBT after it has been heated by a large DC drive current (50, 40 and 30 nA for run 1, 2 and 3, respectively). Fitting to an exponential decay (solid line) yields a time constant of 570 s and a saturation temperature of 3.8 mK. (c) Schematic of the immersion cell used to cool a CBT in the 3He/4He mixture of a dilution refrigerator.

Full size image

A second CBT was immersed in the 3He/4He refrigerant of the custom dilution refrigerator to improve thermal coupling and better isolate external sources of heating. A schematic of the immersion cell is shown in the Fig. 3c. Sintered silver blocks increase the thermal contact between the refrigerant and the incoming contact wires2. Several sinters are attached to the sensor package, to each of the four measurement wires and to a grounding wire for the package and the RC filters. The immersed CBT is found to equilibrate much faster, as shown in Fig. 3a, reaching Te≈3.8 mK at Tmxc≈2.7 mK. It is important to note that even when Te is elevated above Tp and Tmxc, the CBT remains a primary thermometer of its internal electron temperature.

To study the CBT at , the time needed for the sensor to reach thermal equilibrium after a change of Joule heating needs to be known. Figure 3b shows the relaxation of Te after the CBT has been heated by a large drive current for long enough to reach thermal equilibrium (>30 min). The subsequent value of Te is measured by scanning close to VDC=0, where Joule heating should be negligible. The relaxation of Te is found to have a time constant of 570 s.

Figure 4a shows the calibration of the immersed sensor. The three warmest measurements are fitted simultaneously to determine CΣ=209.5 fF and RT=23.21 kΩ. The fitted temperatures agree with Tmxc to within 6%. Given the agreement between the fitted and Tmxc, we can assume that parasitic heating is still negligible down to 10 mK.

Figure 4: Characteristics of a CBT immersed in 3He/4He refrigerant.
figure 4

(a) Fitting to the warmest three measurements gives CΣ=209.5 fF and RT=23.21 kΩ. The fitted minimum electron temperatures for the warmest three curves are in reasonable agreement with the refrigerator temperatures as measured by the vibrating wire resonator (VWR) thermometer: 29.4, 19.0 and 10.5 mK, respectively. (b) Measured electron temperature in the CBT as the refrigerator cooled steadily from 10 to 2.7 mK over a period of 12 h. The solid curve shows a fit of the form , yielding an exponent x=2.7. The dot-dashed curve shows a best fit of . The dashed line shows Te=Tmxc. (c) The measured Te as the refrigerator was temporarily cooled in single-shot mode to 2.2 mK, reaching a lowest Te below 3.7 mK.

Full size image

The coldest measurement in Fig. 4a is fitted using the above values, yielding a minimum electron temperature of 3.86±0.01 mK. This measurement was made over a period of 7 h, to ensure that the CBT was in thermal equilibrium at each value of VDC. At these temperatures, the parasitic heating of the CBT is now significant and does not match the refrigerator temperature of Tmxc=2.7 mK. To fit this conductance dip, the thermal model, equation 3, is used with Tp=Tmxc, and with the parasitic heating P0 and the electron–phonon coupling ΣΩ as free parameters.

Figure 4b shows how the CBT electron temperature diverges from the refrigerator temperature below ≈7 mK. Here the value of Te is found by measuring G0 close to VDC=0 and so Joule heating can be neglected. The lowest temperature reported by the CBT is below 3.7 mK when operating the fridge in single-shot mode (see Fig. 4c).

Discussion

The overheating of the sensor at VDC=0 constrains the value of P0(ΣΩ)−1 in the fit to the coldest measurement in Fig. 4a. However, the parasitic heating is not large enough to reliably separate the values of P0 and ΣΩ in the fitting. Qualitatively, the fits suggest that P0≥300aW per island and ΣΩ is at least four times larger than expected from the nominal size of the thermalization blocks and the literature value of Σ for Au17. It is not possible to determine an upper bound on P0 without constraining ΣΩ. It is worth noting that the power required to measure the CBT conductance (∼1aW per island due to Joule heating from IAC) is much lower than our estimate of P0. As such, we believe that CBTs of this type can be operated at still lower temperatures by further reducing the parasitic heating.

The functional form of Te versus Tmxc, as shown in Fig. 4b, should have the same temperature dependence as the dominant thermalization mechanism, that is, T5 for electron–phonon coupling. However, other power laws have been observed9. Here we find that the best fit of gives x=2.7 and a saturated Te of c1/x=3.4 mK. The fitted exponent x cannot be confirmed by fits to the conductance dips in Fig. 4a, because the overheating is still relatively weak, even at the lowest temperatures, and there is little effect on the shape of the dip. We find that a thermal model with a T3 thermalization term fits the conductance dips equally well as a model using T5.

The saturation of the measured CBT temperature below 7 mK could be caused by parasitic heating of the islands or excess voltage noise across the tunnel junctions. It is possible that the operating temperature could be lowered by reducing parasitic heating through better shielding and by lowering the voltage noise in the measurement circuit. To understand the cause of saturation in more detail, or to test an improved measurement environment, this sensor would need to be cooled closer to 1 mK.

In conclusion, the CBTs described here have been shown to operate as reliable primary thermometers of electron temperature down to 3.7 mK. The large thermalization blocks incorporated in the device and a relatively low level of parasitic heating ensure that the electron subsystem in the sensor is well coupled to the phonon subsystem down to ≈7 mK. An immersion cell is shown to improve thermal coupling between a CBT and a dilution refrigerator. This allows the onset of overheating to be observed below 7 mK, and although the presence of overheating can be seen, the effect is sufficiently weak that the sensor will need to be cooled further to fully characterize the thermalization mechanisms.

Methods

Device fabrication

The CBT devices are fabricated using an ex situ tunnel junction process11. The Al films that define the CBT circuit have a thickness of 250 nm. Tunnel junctions between sections of Al are formed by an insulating layer of 250 nm SiOx deposited by plasma-enhanced chemical vapour deposition (PECVD). The junctions have a nominal diameter 0.8 μm and a resistivity ∼10 kΩ μm2. The substrate is undoped Si with 300 nm thermal oxide on the surface.

The island thickness achievable with the ex situ tunnel junction process or other deposition techniques used for tunnel junction devices is typically up to 1 μm. Thicker films suffer from stress build-up, causing poor adhesion between the film and the substrate. This is a severe problem at mK temperatures where poor adhesion can lead to poor thermalization and even mechanical failure due to thermal motion during cool down. We avoid these problems by using a combination of the ex situ process followed by masked electroplating of Au on top of the CBT islands22, which we refer to as thermalization blocks. Electroplating can produce ∼10 μm-thick, low-stress films and here we choose a nominal thickness of 5 μm for the thermalization blocks.

Refrigerator thermometry

Two different dilution refrigerators are used in the experiments described above. In the commercial refrigerator, the mixing chamber temperature Tmxc is measured by a calibrated RuO2 resistor (Sensor model RU-1000-BF0.007 supplied and calibrated by Bluefors Cryogenics) in contact with the mixing chamber plate. In the custom refrigerator, Tmxc is measured using a conventional vibrating wire resonator viscometer immersed in the saturated dilute phase of the 3He/4He refrigerant in the mixing chamber23,24. The vibrating wire resonator is validated by comparison with a calibrated RuO2 resistor (calibrated to 20 mK and supplied by Lake Shore Cryogenics). This resistor is thermally connected to the refrigerant via an immersed pad of sintered silver.

Data and software availability

All data used in this paper are available at http://dx.doi.org/10.17635/lancaster/researchdata/31, including descriptions of the data sets. The python-based pyCBT software library is freely available from Aivon Oy at https://github.com/AivonOy/pyCBT.

Additional information

How to cite this article: Bradley, D. I. et al. Nanoelectronic primary thermometry below 4 mK. Nat. Commun. 7:10455 doi: 10.1038/ncomms10455 (2016).