Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Tension between reducing sea-level rise and global warming through solar-radiation management

Nature Climate Change volume 2, pages 97–100 (2012)Cite this article

Subjects

Abstract

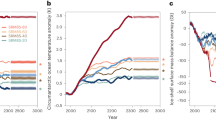
Geoengineering using solar-radiation management (SRM) is gaining interest as a potential strategy to reduce future climate change impacts1,2,3. Basic physics and past observations suggest that reducing insolation will, on average, cool the Earth. It is uncertain, however, whether SRM can reduce climate change stressors such as sea-level rise or rates of surface air temperature change1,4,5,6. Here we use an Earth system model of intermediate complexity to quantify the possible response of sea levels and surface air temperatures to projected climate forcings7 and SRM strategies. We find that SRM strategies introduce a potentially strong tension between the objectives to reduce (1) the rate of temperature change and (2) sea-level rise. This tension arises primarily because surface air temperatures respond faster to radiative forcings than sea levels. Our results show that the forcing required to stop sea-level rise could cause a rapid cooling with a rate similar to the peak business-as-usual warming rate. Furthermore, termination of SRM was found to produce warming rates up to five times greater than the maximum rates under the business-as-usual CO2 scenario, whereas sea-level rise rates were only 30% higher. Reducing these risks requires a slow phase-out of many decades and thus commits future generations.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Hindcasts and projections of surface air temperature, rate of temperature change, and sea-level rise.
Figure 2: Sensitivity of global average temperature and sea-level rise to controls on the geoengineering scenarios.
Figure 3: The maximum warming rate for the period 2030–2100 as a function of the target forcing and the rate of phase-out.
Figure 4: The response of the maximum rate of temperature change and the maximum sea-level rise to the SRM scenarios.

Similar content being viewed by others

References

  1. Wigley, T. M. L. A combined mitigation/geoengineering approach to climate stabilization. Science 314, 452–454 (2006).

    Article  CAS  Google Scholar 

  2. Robock, A., Oman, L. & Stenchikov, G. L. Regional climate responses to geoengineering with tropical and Arctic SO2 injections. J. Geophys. Res. 113, D16101 (2008).

    Article  Google Scholar 

  3. Crutzen, P. J. Albedo enhancement by stratospheric sulphur injections: A contribution to resolve a policy dilemma? Climatic Change 77, 211–219 (2006).

    Article  CAS  Google Scholar 

  4. Jones, A., Haywood, J. & Boucher, O. A comparison of the climate impacts of geoengineering by stratospheric SO2 injection and by brightening of marine stratocumulus cloud. Atmos. Sci. Lett. 12, 176–183 (2011).

    Article  Google Scholar 

  5. Bala, G., Duffy, P. B. & Taylor, K. E. Impact of geoengineering schemes on the global hydrological cycle. Proc. Natl Acad. Sci. USA 105, 7664–7669 (2008).

    Article  CAS  Google Scholar 

  6. Goes, M., Tuana, N. & Keller, K. The economics (or lack thereof) of aerosol geoengineering. Climatic Change 109, 719–744 (2011).

    Article  Google Scholar 

  7. Moss, R. H. et al. The next generation of scenarios for climate change research and assessment. Nature 463, 747–756 (2010).

    Article  CAS  Google Scholar 

  8. Shepherd, J. et al. Geoengineering the Climate: Science, Governace and Uncertainty (The Royal Society, 2009).

    Google Scholar 

  9. Matthews, H. D. & Caldeira, K. Transient climate-carbon simulations of planetary geoengineering. Proc. Natl Acad. Sci. USA 104, 9949–9954 (2007).

    Article  CAS  Google Scholar 

  10. Lunt, D. J., Ridgwell, A., Valdes, P. J. & Seale, A. ‘Sunshade World’: A fully coupled GCM evaluation of the climatic impacts of geoengineering. Geophys. Res. Lett. 35, L12710 (2008).

    Article  Google Scholar 

  11. Latham, J. et al. Global temperature stabilization via controlled albedo enhancement of low-level maritime clouds. Phil. Trans. R. Soc. A 366, 3969–3987 (2008).

    Article  Google Scholar 

  12. Ricke, K. L., Morgan, M. G. & Allen, M. R. Regional climate response to solar-radiation management. Nature Geosci. 3, 537–541 (2010).

    Article  CAS  Google Scholar 

  13. Moore, J. C., Jevrejeva, S. & Grinsted, A. Efficacy of geoengineering to limit twenty first century sea-level rise. Proc. Natl Acad. Sci. USA 107, 15699–15703 (2010).

    Article  CAS  Google Scholar 

  14. Barrett, S. The incredible economics of geoengineering. Environ. Res. Econom. 39, 45–54 (2008).

    Article  Google Scholar 

  15. Moreno-Cruz, J. B., Ricke, K. L. & Keith, D. W. A simple model to account for regional inequalities in the effectiveness of solar radiation management. Climatic Change http://dx.doi.org10.1007/s10584-011-0103-z (2011).

  16. Schelling, T. C. The economic diplomacy of geoengineering. Climatic Change 33, 303–307 (1996).

    Article  Google Scholar 

  17. Millard-Ball, A. The Tuvalu Syndrome Can Geoengineering solve climate’s collective action problem? Climate Change http://dx.doi.org/10.1007/s10584-10011-10102-10580 (2011).

  18. Lempert, R. J., Schlesinger, M. E., Bankes, S. C. & Andronova, N. G. The impacts of climate variability on near-term policy choices and the value of information. Climatic Change 45, 129–161 (2000).

    Article  Google Scholar 

  19. van Dantzig, D. Economic decision problems for flood prevention. Econometrica 24, 276–287 (1956).

    Article  Google Scholar 

  20. Meehl, G. A. et al. in IPCC Climate Change 2007: The Physical Science Basis (eds Solomon, S. et al.) (Cambridge Univ. Press, 2007).

    Google Scholar 

  21. Weaver, A. J. et al. The UVic Earth System Climate Model: Model description, climatology, and applications to past, present and future climates. Atmos.-Ocean 39, 361–428 (2001).

    Article  Google Scholar 

  22. Goes, M. et al. What is the skill of different ocean tracers in reducing uncertainties about projections of the Atlantic Meridional Overturning Circulation. J. Geophys. Res. 115, C12006.

  23. Lenton, T. M. & Vaughan, N. E. The radiative forcing potential of different climate geoengineering options. Atmos. Chem. Phys. 9, 5539–5561 (2009).

    Article  CAS  Google Scholar 

  24. Yohe, G. W. Uncertainty, short-term hedging and the tolerable window approach. Glob. Environ. Change Human Policy Dim. 7, 303–315 (1997).

    Article  Google Scholar 

  25. Jevrejeva, S., Grinsted, A., Moore, J. C. & Holgate, S. Nonlinear trends and multiyear cycles in sea level records. J. Geophys. Res. 111, C09012 (2006).

    Article  Google Scholar 

  26. Brohan, P., Kennedy, J. J., Harris, I., Tett, S. F. B. & Jones, P. D. Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850. J. Geophys. Res. 111, D12106 (2006).

    Article  Google Scholar 

Download references

Acknowledgements

This study was partially supported by the World University Network, the Penn State Center for Climate Risk Management, and the Center for Climate and Energy Decision Making (SES-0949710, through a cooperative agreement between the National Science Foundation and Carnegie Mellon University). P.J.I. acknowledges support from a Natural Environment Research Council PhD studentship. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the funding entities.

Author information

Authors and Affiliations

  1. School of Geographical Sciences, University of Bristol, University Road, Bristol BS8 1SS, UK

    P. J. Irvine

  2. Department of Geosciences, Pennsylvania State University, University Park, Pennsylvania 16802, USA

    R. L. Sriver & K. Keller

Authors
  1. P. J. Irvine
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. L. Sriver
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. Keller
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors jointly designed the study and wrote the paper. P.J.I. performed the model simulations and data analyses.

Corresponding author

Correspondence to P. J. Irvine.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Rights and permissions

Reprints and permissions

About this article

Cite this article

Irvine, P., Sriver, R. & Keller, K. Tension between reducing sea-level rise and global warming through solar-radiation management. Nature Clim Change 2, 97–100 (2012). https://doi.org/10.1038/nclimate1351

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nclimate1351

This article is cited by

Search

Advanced search

Quick links

Nature Briefing Anthropocene

Sign up for the Nature Briefing: Anthropocene newsletter — what matters in anthropocene research, free to your inbox weekly.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing: Anthropocene