Abstract
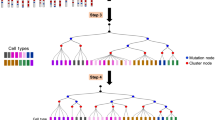
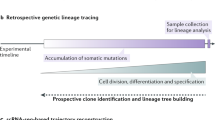
A key goal of developmental biology is to understand how a single cell is transformed into a full-grown organism comprising many different cell types. Single-cell RNA-sequencing (scRNA-seq) is commonly used to identify cell types in a tissue or organ1. However, organizing the resulting taxonomy of cell types into lineage trees to understand the developmental origin of cells remains challenging. Here we present LINNAEUS (lineage tracing by nuclease-activated editing of ubiquitous sequences)—a strategy for simultaneous lineage tracing and transcriptome profiling in thousands of single cells. By combining scRNA-seq with computational analysis of lineage barcodes, generated by genome editing of transgenic reporter genes, we reconstruct developmental lineage trees in zebrafish larvae, and in heart, liver, pancreas, and telencephalon of adult fish. LINNAEUS provides a systematic approach for tracing the origin of novel cell types, or known cell types under different conditions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
$209.00 per year
only $17.42 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Grün, D. & van Oudenaarden, A. Design and analysis of single-cell sequencing experiments. Cell 163, 799–810 (2015).
Woodworth, M.B., Girskis, K.M. & Walsh, C.A. Building a lineage from single cells: genetic techniques for cell lineage tracking. Nat. Rev. Genet. 18, 230–244 (2017).
Spanjaard, B. & Junker, J.P. Methods for lineage tracing on the organism-wide level. Curr. Opin. Cell Biol. 49, 16–21 (2017).
Trapnell, C. et al. The dynamics and regulators of cell fate decisions are revealed by pseudotemporal ordering of single cells. Nat. Biotechnol. 32, 381–386 (2014).
Setty, M. et al. Wishbone identifies bifurcating developmental trajectories from single-cell data. Nat. Biotechnol. 34, 637–645 (2016).
Haghverdi, L., Büttner, M., Wolf, F.A., Buettner, F. & Theis, F.J. Diffusion pseudotime robustly reconstructs lineage branching. Nat. Methods 13, 845–848 (2016).
Barker, N. et al. Identification of stem cells in small intestine and colon by marker gene Lgr5. Nature 449, 1003–1007 (2007).
Livet, J. et al. Transgenic strategies for combinatorial expression of fluorescent proteins in the nervous system. Nature 450, 56–62 (2007).
Lu, R., Neff, N.F., Quake, S.R. & Weissman, I.L. Tracking single hematopoietic stem cells in vivo using high-throughput sequencing in conjunction with viral genetic barcoding. Nat. Biotechnol. 29, 928–933 (2011).
Naik, S.H. et al. Diverse and heritable lineage imprinting of early haematopoietic progenitors. Nature 496, 229–232 (2013).
Sun, J. et al. Clonal dynamics of native haematopoiesis. Nature 514, 322–327 (2014).
Frumkin, D., Wasserstrom, A., Kaplan, S., Feige, U. & Shapiro, E. Genomic variability within an organism exposes its cell lineage tree. PLoS Comput. Biol. 1, e50 (2005).
Lodato, M.A. et al. Somatic mutation in single human neurons tracks developmental and transcriptional history. Science 350, 94–98 (2015).
Ju, Y.S. et al. Somatic mutations reveal asymmetric cellular dynamics in the early human embryo. Nature 543, 714–718 (2017).
Pei, W. et al. Polylox barcoding reveals haematopoietic stem cell fates realized in vivo. Nature 548, 456–460 (2017).
McKenna, A. et al. Whole-organism lineage tracing by combinatorial and cumulative genome editing. Science 353, aaf7907 (2016).
Frieda, K.L. et al. Synthetic recording and in situ readout of lineage information in single cells. Nature 541, 107–111 (2017).
Junker, J.P. et al. Massively parallel clonal analysis using CRISPR/Cas9 induced genetic scars. Preprint at bioRxiv https://doi.org/10.1101/056499 (2017).
Schmidt, S.T., Zimmerman, S.M., Wang, J., Kim, S.K. & Quake, S.R. Quantitative analysis of synthetic cell lineage tracing using nuclease barcoding. ACS Synth. Biol. 6, 936–942 (2017).
Pan, Y.A. et al. Zebrabow: multispectral cell labeling for cell tracing and lineage analysis in zebrafish. Development 140, 2835–2846 (2013).
Klein, A.M. et al. Droplet barcoding for single-cell transcriptomics applied to embryonic stem cells. Cell 161, 1187–1201 (2015).
Satija, R., Farrell, J.A., Gennert, D., Schier, A.F. & Regev, A. Spatial reconstruction of single-cell gene expression data. Nat. Biotechnol. 33, 495–502 (2015).
Villarreal, D.D. et al. Microhomology directs diverse DNA break repair pathways and chromosomal translocations. PLoS Genet. 8, e1003026 (2012).
Schier, A.F. & Talbot, W.S. Molecular genetics of axis formation in zebrafish. Annu. Rev. Genet. 39, 561–613 (2005).
Wiens, J.J. Missing data and the design of phylogenetic analyses. J. Biomed. Inform. 39, 34–42 (2006).
Jagannathan-Bogdan, M. & Zon, L.I. Hematopoiesis. Development 140, 2463–2467 (2013).
Kimmel, C.B. & Warga, R.M. Indeterminate cell lineage of the zebrafish embryo. Dev. Biol. 124, 269–280 (1987).
Keegan, B.R., Meyer, D. & Yelon, D. Organization of cardiac chamber progenitors in the zebrafish blastula. Development 131, 3081–3091 (2004).
Alemany, A. et al. Whole-organism clone tracing using single-cell sequencing. Nature doi:10.1038/nature25969 (2018).
Raj, B. et al. Simultaneous single-cell profiling of lineages and cell types in the vertebrate brain. Nat. Biotechnol. doi:10.1038/nbt.4103 (2018).
Kivioja, T. et al. Counting absolute numbers of molecules using unique molecular identifiers. Nat. Methods 9, 72–74 (2012).
Li, H. Aligning sequence reads, clone sequences and assembly contigs with BWA-MEM. Preprint at https://arxiv.org/abs/1303.3997 (2013).
Wang, G.C. & Wang, Y. Frequency of formation of chimeric molecules as a consequence of PCR coamplification of 16S rRNA genes from mixed bacterial genomes. Appl. Environ. Microbiol. 63, 4645–4650 (1997).
Waltman, L. & van Eck, N.J. A smart local moving algorithm for large-scale modularity-based community detection. Eur. Phys. J. B 86, 471 (2013).
van der Maaten, L. & Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605 (2008).
Amir, A.D. et al. viSNE enables visualization of high dimensional single-cell data and reveals phenotypic heterogeneity of leukemia. Nat. Biotechnol. 31, 545–552 (2013).
McDavid, A. et al. Data exploration, quality control and testing in single-cell qPCR-based gene expression experiments. Bioinformatics 29, 461–467 (2013).
Howe, D.G. et al. ZFIN, the Zebrafish Model Organism Database: increased support for mutants and transgenics. Nucleic Acids Res. 41, D854–D860 (2013).
Kane, D.A. & Kimmel, C.B. The zebrafish midblastula transition. Development 119, 447–456 (1993).
Kobitski, A.Y. et al. An ensemble-averaged, cell density-based digital model of zebrafish embryo development derived from light-sheet microscopy data with single-cell resolution. Sci. Rep. 5, 8601–8610 (2015).
Acknowledgements
We thank R. Opitz, M. Guedes Simoes, D. Panakova, T. Durovic, and J. Ninkovic for help with cell-type identification. We also acknowledge support by MDC/BIMSB core facilities (zebrafish, genomics, bioinformatics), and we thank J. Richter for help with zebrafish experiments. Work in J.P.J.'s laboratory was funded by a European Research Council Starting Grant (ERC-StG 715361 SPACEVAR), a Fondation Leducq Transatlantic Networks Grant (16CVD03), and a Helmholtz Incubator grant (Sparse2Big ZT-I-0007). B.H. was supported by a PhD fellowship from Studienstiftung des deutschen Volkes.
Author information
Authors and Affiliations
Contributions
J.P.J., B.S. and B.H. conceived and designed the project. B.H., N.M. and S.J. optimized dissection and dissociation protocols. B.H. developed the experimental approach for combined scar and transcriptome detection, and B.H. and N.M. performed experiments. B.S. developed computational methods and analyzed the data, with support by P.O.-C. J.P.J. and N.N. guided experiments, and J.P.J. guided analysis. J.P.J. and B.S. wrote the manuscript, with input from all other authors. All authors discussed and interpreted results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Text and Figures
Supplementary Figures 1–20, Supplementary Table 1 and Supplementary Note 1 (PDF 13066 kb)
Supplementary Dataset 1
Technical information for all sequenced libraries (XLSX 10 kb)
Supplementary Dataset 2
Cell type information for 5 dpf larvae (XLSX 40 kb)
Supplementary Dataset 3
Scar detection statistics for 5 dpf larvae (XLSX 14 kb)
Supplementary Dataset 4
Cell type information for adult organs (XLSX 40 kb)
Supplementary Dataset 5
Scar detection statistics for adult organs (XLSX 13 kb)
Supplementary Dataset 6
Statistics connection enrichment analysis (XLSX 146 kb)
Rights and permissions
About this article
Cite this article
Spanjaard, B., Hu, B., Mitic, N. et al. Simultaneous lineage tracing and cell-type identification using CRISPR–Cas9-induced genetic scars. Nat Biotechnol 36, 469–473 (2018). https://doi.org/10.1038/nbt.4124
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nbt.4124
This article is cited by
-
The implications of single-cell RNA-seq analysis in prostate cancer: unraveling tumor heterogeneity, therapeutic implications and pathways towards personalized therapy
Military Medical Research (2024)
-
Dissecting the spatiotemporal diversity of adult neural stem cells
Molecular Systems Biology (2024)
-
Extracting, filtering and simulating cellular barcodes using CellBarcode tools
Nature Computational Science (2024)
-
Developmental progression of DNA double-strand break repair deciphered by a single-allele resolution mutation classifier
Nature Communications (2024)
-
Gene-expression memory-based prediction of cell lineages from scRNA-seq datasets
Nature Communications (2024)