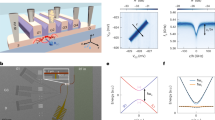
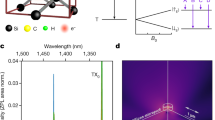
Abstract
Electron spins in silicon quantum dots are attractive systems for quantum computing owing to their long coherence times and the promise of rapid scaling of the number of dots in a system using semiconductor fabrication techniques. Although nearest-neighbour exchange coupling of two spins has been demonstrated, the interaction of spins via microwave-frequency photons could enable long-distance spin–spin coupling and connections between arbitrary pairs of qubits (‘all-to-all’ connectivity) in a spin-based quantum processor. Realizing coherent spin–photon coupling is challenging because of the small magnetic-dipole moment of a single spin, which limits magnetic-dipole coupling rates to less than 1 kilohertz. Here we demonstrate strong coupling between a single spin in silicon and a single microwave-frequency photon, with spin–photon coupling rates of more than 10 megahertz. The mechanism that enables the coherent spin–photon interactions is based on spin–charge hybridization in the presence of a magnetic-field gradient. In addition to spin–photon coupling, we demonstrate coherent control and dispersive readout of a single spin. These results open up a direct path to entangling single spins using microwave-frequency photons.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Tyryshkin, A. M. et al. Electron spin coherence exceeding seconds in high-purity silicon. Nat. Mater. 11, 143–147 (2012)
Saeedi, K. et al. Room-temperature quantum bit storage exceeding 39 minutes using ionized donors in silicon-28. Science 342, 830–833 (2013)
Loss, D. & DiVincenzo, D. P. Quantum computation with quantum dots. Phys. Rev. A 57, 120–126 (1998)
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005)
Neumann, P. et al. Multipartite entanglement among single spins in diamond. Science 320, 1326–1329 (2008)
Dehollain, J. P. et al. Bell’s inequality violation with spins in silicon. Nat. Nanotechnol. 11, 242–246 (2016)
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961–1019 (2013)
Veldhorst, M. et al. An addressable quantum dot qubit with fault-tolerant control-fidelity. Nat. Nanotechnol. 9, 981–985 (2014)
Takeda, K. et al. A fault-tolerant addressable spin qubit in a natural silicon quantum dot. Sci. Adv. 2, e1600694 (2016)
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015)
Zajac, D. M. et al. Resonantly driven CNOT gate for electron spins. Science 359, 439–442 (2018)
Watson, T. F. et al. A programmable two-qubit quantum processor in silicon. Nature https://doi.org/10.1038/nature25766 (2018)
McNeil, R. P. G. et al. On-demand single-electron transfer between distant quantum dots. Nature 477, 439–442 (2011)
Baart, T. A. et al. Single-spin CCD. Nat. Nanotechnol. 11, 330–334 (2016)
Bertrand, B. et al. Fast spin information transfer between distant quantum dots using individual electrons. Nat. Nanotechnol. 11, 672–676 (2016)
Flentje, H. et al. Coherent long-distance displacement of individual electron spins. Nat. Commun. 8, 501 (2017)
Baart, T. A., Fujita, T., Reichl, C., Wegscheider, W. & Vandersypen, L. M. K. Coherent spin-exchange via a quantum mediator. Nat. Nanotechnol. 12, 26–30 (2016)
Bruhat, L. E . et al. Strong coupling between an electron in a quantum dot circuit and a photon in a cavity. Preprint at https://arxiv.org/abs/1612.05214 (2016)
Mi, X., Cady, J. V., Zajac, D. M., Deelman, P. W. & Petta, J. R. Strong coupling of a single electron in silicon to a microwave photon. Science 355, 156–158 (2017)
Stockklauser, A. et al. Strong coupling cavity QED with gate-defined double quantum dots enabled by a high impedance resonator. Phys. Rev. X 7, 011030 (2017)
Thompson, R. J., Rempe, G. & Kimble, H. J. Observation of normal-mode splitting for an atom in an optical cavity. Phys. Rev. Lett. 68, 1132–1135 (1992)
Brune, M. et al. Quantum Rabi oscillation: a direct test of field quantization in a cavity. Phys. Rev. Lett. 76, 1800–1803 (1996)
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004)
Blais, A., Huang, R.-S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: an architecture for quantum computation. Phys. Rev. A 69, 062320 (2004)
Childress, L., Sorensen, A. S. & Lukin, M. D. Mesoscopic cavity quantum electrodynamics with quantum dots. Phys. Rev. A 69, 042302 (2004)
Imamoğlu, A. Cavity QED based on collective magnetic dipole coupling: spin ensembles as hybrid two-level systems. Phys. Rev. Lett. 102, 083602 (2009)
Schuster, D. I. et al. High-cooperativity coupling of electron-spin ensembles to superconducting cavities. Phys. Rev. Lett. 105, 140501 (2010)
Amsüss, R. et al. Cavity QED with magnetically coupled collective spin states. Phys. Rev. Lett. 107, 060502 (2011)
Bienfait, A. et al. Controlling spin relaxation with a cavity. Nature 531, 74–77 (2016)
Eichler, C. et al. Electron spin resonance at the level of 104 spins using low impedance superconducting resonators. Phys. Rev. Lett. 118, 037701 (2017)
Trif, M., Golovach, V. N. & Loss, D. Spin dynamics in InAs nanowire quantum dots coupled to a transmission line. Phys. Rev. B 77, 045434 (2008)
Cottet, A. & Kontos, T. Spin quantum bit with ferromagnetic contacts for circuit QED. Phys. Rev. Lett. 105, 160502 (2010)
Hu, X., Liu, Y.-x. & Nori, F. Strong coupling of a spin qubit to a superconducting stripline cavity. Phys. Rev. B 86, 035314 (2012)
Beaudoin, F., Lachance-Quirion, D., Coish, W. A. & Pioro-Ladriere, M. Coupling a single electron spin to a microwave resonator: controlling transverse and longitudinal couplings. Nanotechnology 27, 464003 (2016)
Frey, T. et al. Dipole coupling of a double quantum dot to a microwave resonator. Phys. Rev. Lett. 108, 046807 (2012)
Petersson, K. D. et al. Circuit quantum electrodynamics with a spin qubit. Nature 490, 380–383 (2012)
Viennot, J. J., Dartiailh, M. C., Cottet, A. & Kontos, T. Coherent coupling of a single spin to microwave cavity photons. Science 349, 408–411 (2015)
Kawakami, E. et al. Electrical control of a long-lived spin qubit in a Si/SiGe quantum dot. Nat. Nanotechnol. 9, 666–670 (2014)
Burkard, G. & Imamoglu, A. Ultra-long-distance interaction between spin qubits. Phys. Rev. B 74, 041307 (2006)
Jin, P.-Q., Marthaler, M., Shnirman, A. & Schon, G. Strong coupling of spin qubits to a transmission line resonator. Phys. Rev. Lett. 108, 190506 (2012)
Benito, M., Mi, X., Taylor, J. M., Petta, J. R. & Burkard, G. Input-output theory for spin-photon coupling in Si double quantum dots. Phys. Rev. B 96, 235434 (2017)
Schuster, D. I. et al. ac Stark shift and dephasing of a superconducting qubit strongly coupled to a cavity field. Phys. Rev. Lett. 94, 123602 (2005)
Mi, X. et al. Circuit quantum electrodynamics architecture for gate-defined quantum dots in silicon. Appl. Phys. Lett. 110, 043502 (2017)
Mi, X., Peterfalvi, C. G., Burkard, G. & Petta, J. R. High-resolution valley spectroscopy of Si quantum dots. Phys. Rev. Lett. 119, 176803 (2017)
Probst, S. et al. Inductive-detection electron-spin resonance spectroscopy with 65 spins/√Hz sensitivity. Appl. Phys. Lett. 111, 202604 (2017)
Majer, J. et al. Coupling superconducting qubits via a cavity bus. Nature 449, 443–447 (2007)
Sillanpää, M. A., Park, J. I. & Simmonds, R. W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 449, 438–442 (2007)
Zajac, D. M., Hazard, T. M., Mi, X., Wang, K. & Petta, J. R. A reconfigurable gate architecture for Si/SiGe quantum dots. Appl. Phys. Lett. 106, 223507 (2015)
Elzerman, J. M. et al. Single-shot read-out of an individual electron spin in a quantum dot. Nature 430, 431–435 (2004)
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012)
Debnath, S. et al. Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66 (2016)
Nigg, S. E ., Fuhrer, A . & Loss, D. Superconducting grid-bus surface code architecture for hole-spin qubits. Phys. Rev. Lett. 118, 147701 (2017)
Samkharadze, N . et al. Strong spin-photon coupling in silicon. Preprint at https://arxiv.org/abs/1711.02040 (2017)
Landig, A. J . et al. Coherent spin-qubit photon coupling. Preprint at https://arxiv.org/abs/1711.01932 (2017)
Wallraff, A. et al. Approaching unit visibility for control of a superconducting qubit with dispersive readout. Phys. Rev. Lett. 95, 060501 (2005)
Wallraff, A., Stockklauser, A., Ihn, T., Petta, J. R. & Blais, A. Comment on “Vacuum Rabi splitting in a semiconductor circuit QED system”. Phys. Rev. Lett. 111, 249701 (2013)
Rau, I., Johansson, G. & Shnirman, A. Cavity quantum electrodynamics in superconducting circuits: Susceptibility at elevated temperatures. Phys. Rev. B 70, 054521 (2004)
Yoneda, J . et al. A >99:9% fidelity quantum-dot spin qubit with coherence limited by charge noise. Preprint at https://arxiv.org/abs/1708.01454 (2017)
Samkharadze, N. et al. High-kinetic-inductance superconducting nanowire resonators for circuit QED in a magnetic field. Phys. Rev. Appl. 5, 044004 (2016)
Acknowledgements
We thank A. J. Sigillito for technical assistance and M. J. Gullans for discussions. This work was supported by the US Department of Defense under contract H98230-15-C0453, Army Research Office grant W911NF-15-1-0149, and the Gordon and Betty Moore Foundations EPiQS Initiative through grant GBMF4535. Devices were fabricated in the Princeton University Quantum Device Nanofabrication Laboratory.
Author information
Authors and Affiliations
Contributions
X.M. fabricated the sample and performed the measurements. X.M., D.M.Z. and J.R.P. developed the design and fabrication process for the DQD. X.M. and S.P. developed the niobium cavity fabrication process. M.B., G.B., J.M.T. and J.R.P. developed the theory for the experiment. X.M., M.B. and J.M.T. analysed the data. X.M., J.R.P., G.B. and J.M.T. wrote the manuscript with input from the other authors. J.R.P. planned and supervised the experiment.
Corresponding author
Ethics declarations
Competing interests
X.M., J.R.P., D.M.Z. and Princeton University have filed a provisional US patent application related to spin–photon transduction.
Additional information
Reviewer Information Nature thanks T. Meunier and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Extended Data Figure 1 Micromagnet design.
To-scale drawing of the micromagnet design, superimposed on top of the SEM image of the DQD. The coordinate axes and the direction of the externally applied magnetic field  are indicated at the bottom. In this geometry, the DQD electron experiences a homogeneous z field
are indicated at the bottom. In this geometry, the DQD electron experiences a homogeneous z field  . The total x field Bx that is experienced by the electron is spatially dependent, being approximately
. The total x field Bx that is experienced by the electron is spatially dependent, being approximately  (
( ) when the electron is in the L (R) dot (
) when the electron is in the L (R) dot ( ) and
) and  when the electron is delocalized between the DQDs (ε = 0). The y field By for the DQD electron is expected to be small compared to the other field components for this magnet design.
when the electron is delocalized between the DQDs (ε = 0). The y field By for the DQD electron is expected to be small compared to the other field components for this magnet design.
Extended Data Figure 2 Photon number calibration.
The ESR resonance frequency fESR, measured using the phase response of the cavity Δϕ in the dispersive regime (Fig. 4b), is plotted as a function of the estimated power at the input port of the cavity P (data). The device is configured with gs/(2π) = 2.4 MHz and spin–photon detuning Δ/(2π) ≈ −18 MHz. The dashed line shows a fit to  , where nph is the average number of photons in the cavity, plotted as the top x axis. The experiments are conducted with P ≈ −133 dBm (0.05 fW), which corresponds to nph ≈ 0.6. The error bars indicate the uncertainties in the centre frequency of the ESR transition.
, where nph is the average number of photons in the cavity, plotted as the top x axis. The experiments are conducted with P ≈ −133 dBm (0.05 fW), which corresponds to nph ≈ 0.6. The error bars indicate the uncertainties in the centre frequency of the ESR transition.
Extended Data Figure 3 DQD stability diagrams.
The cavity transmission amplitude A/A0 (a, c) and phase response Δϕ (b, d) are plotted as functions of VP1 and VP2 for DQD1 (a, b) and DQD2 (c, d), obtained with f = fc. The (1, 0) ↔ (0, 1) transitions are clearly identified on the basis of these measurements and subsequently tuned close to resonance with the cavity for the experiments described in the main text. The red circles indicate the locations of the (1, 0) ↔ (0, 1) transitions of the two DQDs.
Extended Data Figure 4 Spin decoherence rates at different DQD tunnel couplings.
ESR line, as measured in the cavity phase response Δϕ(fs), is shown for different values of 2tc/h in the low-power limit (data). ε = 0 for every dataset. Dashed lines are fits with Lorentzian functions and γs/(2π) is determined as the half-width at half-maximum of each Lorentzian. The spin–photon detuning |Δ|≈10 gs for each dataset, to ensure that the system is in the dispersive regime.
Extended Data Figure 5 Spin–photon coupling strengths at different DQD tunnel couplings.
a, b, Vacuum Rabi splittings for 2tc/h < fc (a) and 2tc/h > fc (b), obtained by varying  until a pair of resonance peaks with approximately equal heights emerges in the cavity transmission spectrum A/A0. gs/(2π) is then estimated as half the frequency difference between the two peaks. ε = 0 for every dataset. gs is difficult to measure for 5.2 GHz < 2tc/h < 6.7 GHz owing to the small values of A/A0 that arise from the large spin decoherence rates γs in this regime.
until a pair of resonance peaks with approximately equal heights emerges in the cavity transmission spectrum A/A0. gs/(2π) is then estimated as half the frequency difference between the two peaks. ε = 0 for every dataset. gs is difficult to measure for 5.2 GHz < 2tc/h < 6.7 GHz owing to the small values of A/A0 that arise from the large spin decoherence rates γs in this regime.
Extended Data Figure 6 Spin relaxation at ε = 0.
The time-averaged phase response of the cavity Δϕ is shown as a function of wait time TM (data), measured using the pulse sequence illustrated in Fig. 4c. The microwave burst time is fixed at τB = 80 ns. The dashed line shows a fit using the function ϕ0 + ϕ1(T1/TM)[1 − exp(−TM/T1)], which yields a spin relaxation time of T1 ≈ 3.2 μs. The experimental conditions are the same as for Fig. 4d.
Extended Data Figure 7 Theoretical fits to vacuum Rabi splittings.
The calculated cavity transmission spectra (black solid lines) are superimposed on the experimentally measured vacuum Rabi splittings shown in Fig. 2b, c (data). The calculations are produced with gc/(2π) = 40 MHz (gc/(2π) = 37 MHz), κ/(2π) = 1.8 MHz, γc/(2π) = 105 MHz (γc/(2π) = 120 MHz),  ,
,  and 2tc/h = 7.4 GHz for DQD1 (DQD2). For comparison, A(f)/A0, simulated for a two-level charge qubit with a decoherence rate of γc/(2π) = 2.4 MHz coupled to a cavity with κ/(2π) = 1.8 MHz at a rate gc/(2π) = 5.5 MHz, is shown in a for thermal photon numbers of nth = 0.02 (black dashed line) and nth = 0.5 (red dashed line).
and 2tc/h = 7.4 GHz for DQD1 (DQD2). For comparison, A(f)/A0, simulated for a two-level charge qubit with a decoherence rate of γc/(2π) = 2.4 MHz coupled to a cavity with κ/(2π) = 1.8 MHz at a rate gc/(2π) = 5.5 MHz, is shown in a for thermal photon numbers of nth = 0.02 (black dashed line) and nth = 0.5 (red dashed line).
Extended Data Figure 8 Prospect for long-range spin–spin coupling.
Source data
Rights and permissions
About this article
Cite this article
Mi, X., Benito, M., Putz, S. et al. A coherent spin–photon interface in silicon. Nature 555, 599–603 (2018). https://doi.org/10.1038/nature25769
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature25769
This article is cited by
-
Modeling Si/SiGe quantum dot variability induced by interface disorder reconstructed from multiperspective microscopy
npj Quantum Information (2024)
-
Strong coupling between a microwave photon and a singlet-triplet qubit
Nature Communications (2024)
-
Direct manipulation of a superconducting spin qubit strongly coupled to a transmon qubit
Nature Physics (2023)
-
Probing two-qubit capacitive interactions beyond bilinear regime using dual Hamiltonian parameter estimations
npj Quantum Information (2023)
-
Strong coupling between a photon and a hole spin in silicon
Nature Nanotechnology (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.