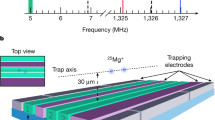
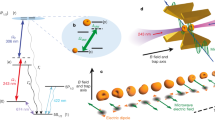
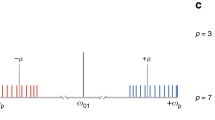
Abstract
Quantum bits (qubits) based on individual trapped atomic ions are a promising technology for building a quantum computer1. The elementary operations necessary to do so have been achieved with the required precision for some error-correction schemes2,3,4. However, the essential two-qubit logic gate that is used to generate quantum entanglement has hitherto always been performed in an adiabatic regime (in which the gate is slow compared with the characteristic motional frequencies of the ions in the trap3,4,5,6,7), resulting in logic speeds of the order of 10 kilohertz. There have been numerous proposals of methods for performing gates faster than this natural ‘speed limit’ of the trap8,9,10,11,12. Here we implement one such method11, which uses amplitude-shaped laser pulses to drive the motion of the ions along trajectories designed so that the gate operation is insensitive to the optical phase of the pulses. This enables fast (megahertz-rate) quantum logic that is robust to fluctuations in the optical phase, which would otherwise be an important source of experimental error. We demonstrate entanglement generation for gate times as short as 480 nanoseconds—less than a single oscillation period of an ion in the trap and eight orders of magnitude shorter than the memory coherence time measured in similar calcium-43 hyperfine qubits. The power of the method is most evident at intermediate timescales, at which it yields a gate error more than ten times lower than can be attained using conventional techniques; for example, we achieve a 1.6-microsecond-duration gate with a fidelity of 99.8 per cent. Faster and higher-fidelity gates are possible at the cost of greater laser intensity. The method requires only a single amplitude-shaped pulse and one pair of beams derived from a continuous-wave laser. It offers the prospect of combining the unrivalled coherence properties2,13, operation fidelities2,3,4 and optical connectivity14 of trapped-ion qubits with the submicrosecond logic speeds that are usually associated with solid-state devices15,16.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Wineland, D. J. et al. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. J. Res. Natl Inst. Stand. Technol. 103, 259–328 (1998)
Harty, T. P. et al. High-fidelity preparation, gates, memory, and readout of a trapped-ion quantum bit. Phys. Rev. Lett. 113, 220501 (2014)
Ballance, C. J. et al. High-fidelity quantum logic gates using trapped-ion hyperfine qubits. Phys. Rev. Lett. 117, 060504 (2016)
Gaebler, J. P. et al. High-fidelity universal gate set for 9Be+ ion qubits. Phys. Rev. Lett. 117, 060505 (2016)
Turchette, Q. A. et al. Deterministic entanglement of two trapped ions. Phys. Rev. Lett. 81, 3631–3634 (1998)
Leibfried, D. et al. Experimental demonstration of a robust, high-fidelity geometric two ion-qubit phase gate. Nature 422, 412–415 (2003)
Benhelm, J. et al. Towards fault-tolerant quantum computing with trapped ions. Nat. Phys. 4, 463–466 (2008)
García-Ripoll, J. J., Zoller, P. & Cirac, J. I. Speed optimized two-qubit gates with laser coherent control techniques for ion trap quantum computing. Phys. Rev. Lett. 91, 157901 (2003)
Duan, L.-M. Scaling ion trap quantum computation through fast quantum gates. Phys. Rev. Lett. 93, 100502 (2004)
García-Ripoll, J. J., Zoller, P. & Cirac, J. I. Coherent control of trapped ions using off-resonant lasers. Phys. Rev. A 71, 062309 (2005)
Steane, A. M. et al. Pulsed force sequences for fast phase-insensitive quantum gates in trapped ions. New J. Phys. 16, 053049 (2014)
Palmero, M. et al. Fast phase gates with trapped ions. Phys. Rev. A 95, 022328 (2017)
Wang, Y. et al. Single-qubit quantum memory exceeding ten-minute coherence time. Nat. Photon. 11, 646–650 (2017)
Moehring, D. L. et al. Entanglement of single-atom quantum bits at a distance. Nature 449, 68–71 (2007)
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014)
Veldhorst, M. et al. A two-qubit logic gate in silicon. Nature 526, 410–414 (2015)
Fowler, A. G. et al. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012)
Monroe, C. & Kim, J. Scaling the ion trap quantum processor. Science 339, 1164–1169 (2013)
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013)
Lin, Y. et al. Sympathetic electromagnetically-induced-transparency laser cooling of motional modes in an ion chain. Phys. Rev. Lett. 110, 153002 (2013)
Bowler, R. et al. Coherent diabatic ion transport and separation in a multizone trap array. Phys. Rev. Lett. 109, 080502 (2012)
Ruster, T. et al. Experimental realization of fast ion separation in segmented Paul traps. Phys. Rev. A 90, 033410 (2014)
Noek, R. et al. High speed, high fidelity detection of an atomic hyperfine qubit. Opt. Lett. 38, 4735–4738 (2013)
Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. Nature 417, 709–711 (2002)
Turchette, Q. A. et al. Heating of trapped ions from the quantum ground state. Phys. Rev. A 61, 063418 (2000)
Ruster, T. et al. A long-lived Zeeman trapped-ion qubit. Appl. Phys. B 122, 254 (2016)
Wong-Campos, J. D., Moses, S. A., Johnson, K. G. & Monroe, C. Demonstration of two-atom entanglement with ultrafast optical pulses. Phys. Rev. Lett. 119, 230501 (2017)
Ozeri, R. et al. Errors in trapped-ion quantum gates due to spontaneous photon scattering. Phys. Rev. A 75, 042329 (2007)
McDonnell, M. J. et al. Long-lived mesoscopic entanglement outside the Lamb-Dicke regime. Phys. Rev. Lett. 98, 063603 (2007)
Schmidt, P. O. et al. Spectroscopy using quantum logic. Science 309, 749–752 (2005)
Meyer, V. et al. Measurement of the 1s–2s energy interval in muonium. Phys. Rev. Lett. 84, 1136–1139 (2000)
Machnes, S. et al. Superfast laser cooling. Phys. Rev. Lett. 104, 183001 (2010)
Schäfer, V. M. et al. Optical injection and spectral filtering of high-power ultraviolet laser diodes. Opt. Lett. 40, 4265–4268 (2015)
Degenhardt, C. et al. Influence of chirped excitation pulses in an optical clock with ultracold calcium atoms. IEEE Trans. Instrum. Meas. 54, 771–775 (2005)
Gulde, S. T. Experimental Realization of Quantum Gates and the Deutsch–Josza Algorithm with Trapped 40Ca+-Ions. PhD thesis, Univ. Innsbruck (2003)
Woodrow, S. R. Linear Paul Trap Design for High-fidelity, Scalable Quantum Information Processing. MSc thesis, Univ. Oxford (2015)
Allcock, D. T. C. et al. Dark-resonance Doppler cooling and high fluorescence in trapped Ca-43 ions at intermediate magnetic field. New J. Phys. 18, 023043 (2016)
Sackett, C. A. et al. Experimental entanglement of four particles. Nature 404, 256–259 (2000)
Acknowledgements
This work was supported by the UK EPSRC ‘Networked Quantum Information Technologies’ Hub, and the UK Defence, Science and Technology Laboratory. V.M.S. acknowledges funding from Balliol College, Oxford. C.J.B. acknowledges funding from Magdalen College, Oxford. We thank S. R. Woodrow for work on the trap design, T. P. Harty for contributions to the apparatus and W. Zhang for the loan of the AWG. We acknowledge the use of the University of Oxford Advanced Research Computing facility (https://doi.org/10.5281/zenodo.22558). The experiments benefitted from the use of the ARTIQ control system (https://doi.org/10.5281/zenodo.591804).
Author information
Authors and Affiliations
Contributions
C.J.B. performed the numerical modelling. V.M.S. and C.J.B. designed and performed the experiments and analysed the data. K.T. built the ion trap and characterized the fast AOMs. L.J.S. and T.G.B. built optical and control systems. V.M.S., C.J.B., A.M.S. and D.M.L. wrote the manuscript, which all authors discussed.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
Rights and permissions
About this article
Cite this article
Schäfer, V., Ballance, C., Thirumalai, K. et al. Fast quantum logic gates with trapped-ion qubits. Nature 555, 75–78 (2018). https://doi.org/10.1038/nature25737
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature25737
This article is cited by
-
Speed limit of quantum metrology
Scientific Reports (2023)
-
Robust oscillator-mediated phase gates driven by low-intensity pulses
Communications Physics (2023)
-
Noisy intermediate-scale quantum computers
Frontiers of Physics (2023)
-
Entangling gates for trapped-ion quantum computation and quantum simulation
Journal of the Korean Physical Society (2023)
-
XIRAC-Q: a near-real-time quantum operating system scheduling structure based on Shannon information theorem
Quantum Information Processing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.