Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level

Nature volume 549, pages 360–364 (2017)Cite this article

Subjects

Abstract

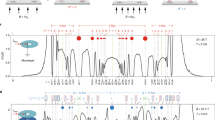
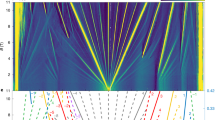
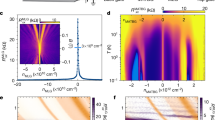
Non-Abelian anyons are a type of quasiparticle with the potential to encode quantum information in topological qubits protected from decoherence1. Experimental systems that are predicted to harbour non-Abelian anyons include p-wave superfluids, superconducting systems with strong spin–orbit coupling, and paired states of interacting composite fermions that emerge at even denominators in the fractional quantum Hall (FQH) regime. Although even-denominator FQH states have been observed in several two-dimensional systems2,3,4, small energy gaps and limited tunability have stymied definitive experimental probes of their non-Abelian nature. Here we report the observation of robust even-denominator FQH phases at half-integer Landau-level filling in van der Waals heterostructures consisting of dual-gated, hexagonal-boron-nitride-encapsulated bilayer graphene. The measured energy gap is three times larger than observed previously3,4. We compare these FQH phases with numerical and theoretical models while simultaneously controlling the carrier density, layer polarization and magnetic field, and find evidence for the paired Pfaffian phase5 that is predicted to host non-Abelian anyons. Electric-field-controlled level crossings between states with different Landau-level indices reveal a cascade of FQH phase transitions, including a continuous phase transition between the even-denominator FQH state and a compressible composite fermion liquid. Our results establish graphene as a pristine and tunable experimental platform for studying the interplay between topology and quantum criticality, and for detecting non-Abelian qubits.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Fractional quantum Hall (FQH) effect in an all van der Waals heterostructure.
Figure 2: The state.
Figure 3: Interlayer correlated FQH states.

Similar content being viewed by others

References

  1. Kitaev, A. Yu. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003)

    Article  CAS  ADS  MathSciNet  Google Scholar 

  2. Willett, R. et al. Observation of an even-denominator quantum number in the fractional quantum Hall effect. Phys. Rev. Lett. 59, 1776–1779 (1987)

    Article  CAS  ADS  Google Scholar 

  3. Ki, D.-K., Fal’ko, V. I., Abanin, D. A. & Morpurgo, A. F. Observation of even denominator fractional quantum Hall effect in suspended bilayer graphene. Nano Lett. 14, 2135–2139 (2014)

    Article  CAS  ADS  Google Scholar 

  4. Falson, J. et al. Even-denominator fractional quantum Hall physics in ZnO. Nat. Phys. 11, 347–351 (2015)

    Article  CAS  Google Scholar 

  5. Moore, G. & Read, N. Nonabelions in the fractional quantum Hall effect. Nucl. Phys. B 360, 362–396 (1991)

    Article  ADS  MathSciNet  Google Scholar 

  6. Jain, J. K. Composite-fermion approach for the fractional quantum Hall effect. Phys. Rev. Lett. 63, 199–202 (1989)

    Article  CAS  ADS  Google Scholar 

  7. Halperin, B. I., Lee, P. A. & Read, N. Theory of the half-filled Landau level. Phys. Rev. B 47, 7312–7343 (1993)

    Article  CAS  ADS  Google Scholar 

  8. Willett, R. L., Ruel, R. R., West, K. W. & Pfeiffer, L. N. Experimental demonstration of a Fermi surface at one-half filling of the lowest Landau level. Phys. Rev. Lett. 71, 3846–3849 (1993)

    Article  CAS  ADS  Google Scholar 

  9. Kang, W., Stormer, H. L., Pfeiffer, L. N., Baldwin, K. W. & West, K. W. How real are composite fermions? Phys. Rev. Lett. 71, 3850–3853 (1993)

    Article  CAS  ADS  Google Scholar 

  10. Read, N. & Green, D. Paired states of fermions in two dimensions with breaking of parity and time-reversal symmetries and the fractional quantum Hall effect. Phys. Rev. B 61, 10267–10297 (2000)

    Article  CAS  ADS  Google Scholar 

  11. Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008)

    Article  CAS  ADS  MathSciNet  Google Scholar 

  12. Papic´, Z. & Abanin, D. A. Topological phases in the zeroth Landau level of bilayer graphene. Phys. Rev. Lett. 112, 046602 (2014)

    Article  ADS  Google Scholar 

  13. Lee, K. et al. Chemical potential and quantum Hall ferromagnetism in bilayer graphene. Science 345, 58–61 (2014)

    Article  CAS  ADS  Google Scholar 

  14. Maher, P. et al. Tunable fractional quantum Hall phases in bilayer graphene. Science 345, 61–64 (2014)

    Article  CAS  ADS  Google Scholar 

  15. Hunt, B. M. et al. Direct measurement of discrete valley and orbital quantum numbers in bilayer graphene. Nat. Commun. (in the press)

  16. Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. Compressibility of the two-dimensional electron gas: measurements of the zero-field exchange energy and fractional quantum Hall gap. Phys. Rev. B 50, 1760–1778 (1994)

    Article  CAS  ADS  Google Scholar 

  17. Levin, M., Halperin, B. I. & Rosenow, B. Particle-hole symmetry and the Pfaffian state. Phys. Rev. Lett. 99, 236806 (2007)

    Article  ADS  Google Scholar 

  18. Lee, S.-S., Ryu, S., Nayak, C. & Fisher, M. P. A. Particle-hole symmetry and the ν = 5/2 quantum Hall state. Phys. Rev. Lett. 99, 236807 (2007)

    Article  ADS  Google Scholar 

  19. Halperin, B. I. Theory of the quantized Hall conductance. Helv. Phys. Acta 56, 75–102 (1983)

    CAS  Google Scholar 

  20. Kumar, A., Csáthy, G. A., Manfra, M. J., Pfeiffer, L. N. & West, K. W. Nonconventional odd-denominator fractional quantum Hall states in the second Landau level. Phys. Rev. Lett. 105, 246808 (2010)

    Article  CAS  ADS  Google Scholar 

  21. Apalkov, V. M. & Chakraborty, T. Stable Pfaffian state in bilayer graphene. Phys. Rev. Lett. 107, 186803 (2011)

    Article  ADS  Google Scholar 

  22. Metlitski, M. A., Mross, D. F., Sachdev, S. & Senthil, T. Cooper pairing in non-Fermi liquids. Phys. Rev. B 91, 115111 (2015)

    Article  ADS  Google Scholar 

  23. Rezayi, H. R. & Simon, S. H. Breaking of particle-hole symmetry by Landau level mixing in the ν = 5/2 quantized Hall State. Phys. Rev. Lett. 106, 116801 (2011)

    Article  ADS  Google Scholar 

  24. Zaletel, M. P., Mong, R. S. K., Pollmann, F. & Rezayi, E. H. Infinite density matrix renormalization group for multicomponent quantum Hall systems. Phys. Rev. B 91, 045115 (2015)

    Article  ADS  Google Scholar 

  25. Rezayi, E. H. Landau level mixing and the ground state of the ν = 5/2 quantum Hall effect. Phys. Rev. Lett. 119, 026801 (2017)

    Article  ADS  Google Scholar 

  26. Levin, M. & Halperin, B. I. Collective states of non-Abelian quasiparticles in a magnetic field. Phys. Rev. B 79, 205301 (2009)

    Article  ADS  Google Scholar 

  27. von Keyserlingk, C. W., Simon, S. H. & Rosenow, B. Enhanced bulk-edge Coulomb coupling in fractional Fabry–Perot interferometers. Phys. Rev. Lett. 115, 126807 (2015)

    Article  CAS  ADS  Google Scholar 

  28. Wei, D. S. Mach–Zehnder interferometry using spin- and valley-polarized quantum Hall edge states in graphene. Sci. Adv. 3, e1700600 (2017)

    Article  ADS  Google Scholar 

  29. Cooper, N. R. & Stern, A. Observable bulk signatures of non-Abelian quantum Hall states. Phys. Rev. Lett. 102, 176807 (2009)

    Article  CAS  ADS  Google Scholar 

  30. Barkeshli, M., Nayak, C., Papic, Z., Young, A. & Zaletel, M. Fractionalized exciton Fermi surfaces and condensates in two-component quantized Hall states. Preprint at https://arxiv.org/abs/1611.01171 (2016)

Download references

Acknowledgements

We acknowledge experimental assistance of B. Odegard and J. Island, and discussions with M. Barkeshli, C. Dean, E.-A. Kim, R. Mong, C. Nayak, Z. Papic, S. Simon and A. Stern. Magnetocapacitance measurements were funded by the NSF under DMR-1636607. A portion of the nanofabrication and the transport measurements were funded by the ARO under proposal 69188PHH. A.F.Y. acknowledges the support of the David and Lucile Packard Foundation. Measurements above 14 T were performed at the National High Magnetic Field Laboratory, which is supported by National Science Foundation cooperative agreement number DMR-1157490 and the State of Florida. The numerical simulations were performed on computational resources supported by the Princeton Institute for Computational Science and Engineering (PICSciE). E.M.S. acknowledges the support of the Elings Fellowship. K.W. and T.T. acknowledge support from the Elemental Strategy Initiative conducted by the MEXT, Japan and JSPS KAKENHI grant number JP15K21722.

Author information

Authors and Affiliations

  1. Department of Physics, University of California, Santa Barbara, 93106, California, USA

    A. A. Zibrov, C. Kometter, H. Zhou & A. F. Young

  2. California Nanosystems Institute, University of California at Santa Barbara, Santa Barbara, 93106, California, USA

    E. M. Spanton

  3. Advanced Materials Laboratory, National Institute for Materials Science, Tsukuba, 305-0044, Ibaraki, Japan

    T. Taniguchi & K. Watanabe

  4. Department of Physics, Princeton University, Princeton, 08544, New Jersey, USA

    M. P. Zaletel

Authors
  1. A. A. Zibrov
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C. Kometter
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. H. Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. E. M. Spanton
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. T. Taniguchi
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. K. Watanabe
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. M. P. Zaletel
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. A. F. Young
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

A.A.Z., E.M.S. and H.Z. fabricated devices A, B and C, respectively. T.T. and K.W. synthesized the hexagonal boron nitride crystals. A.F.Y. and C.K. built the measurement electronics. A.A.Z., H.Z., E.M.S. and A.F.Y. acquired and analysed the experimental data. M.P.Z. performed the DMRG calculations. A.A.Z., M.P.Z. and A.F.Y. wrote the paper.

Corresponding author

Correspondence to A. F. Young.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Additional information

Reviewer Information Nature thanks D. Abanin, K. Park, K. Yang and the other anonymous reviewer(s) for their contribution to the peer review of this work.

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

This file contains methods, figures S1-S17 and tables S1-S3. (PDF 27030 kb)

PowerPoint slides

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zibrov, A., Kometter, C., Zhou, H. et al. Tunable interacting composite fermion phases in a half-filled bilayer-graphene Landau level. Nature 549, 360–364 (2017). https://doi.org/10.1038/nature23893

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature23893

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing