Abstract
Mosquitoes exhibit unusual wing kinematics; their long, slender wings flap at remarkably high frequencies for their size (>800 Hz)and with lower stroke amplitudes than any other insect group1. This shifts weight support away from the translation-dominated, aerodynamic mechanisms used by most insects2, as well as by helicopters and aeroplanes, towards poorly understood rotational mechanisms that occur when pitching at the end of each half-stroke. Here we report free-flight mosquito wing kinematics, solve the full Navier–Stokes equations using computational fluid dynamics with overset grids, and validate our results with in vivo flow measurements. We show that, although mosquitoes use familiar separated flow patterns, much of the aerodynamic force that supports their weight is generated in a manner unlike any previously described for a flying animal. There are three key features: leading-edge vortices (a well-known mechanism that appears to be almost ubiquitous in insect flight), trailing-edge vortices caused by a form of wake capture at stroke reversal, and rotational drag. The two new elements are largely independent of the wing velocity, instead relying on rapid changes in the pitch angle (wing rotation) at the end of each half-stroke, and they are therefore relatively immune to the shallow flapping amplitude. Moreover, these mechanisms are particularly well suited to high aspect ratio mosquito wings.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
Change history
05 April 2017
The y-axis units were corrected in Fig. 3.
References
Simões, P. M. V., Ingham, R. A., Gibson, G. & Russell, I. J. A role for acoustic distortion in novel rapid frequency modulation behaviour in free-flying male mosquitoes. J. Exp. Biol. 219, 2039–2047 (2016)
Chin, D. D. & Lentink, D. Flapping wing aerodynamics: from insects to vertebrates. J. Exp. Biol. 219, 920–932 (2016)
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. Leading-edge vortices in insect flight. Nature 384, 626–630 (1996)
Somps, C. & Luttges, M. Dragonfly flight: novel uses of unsteady separated flows. Science 228, 1326–1329 (1985)
Bomphrey, R. J., Srygley, R. B., Taylor, G. K., Nudds, R. L. & Thomas, A. L. R. Visualising the flow around insect wings. Phys. Fluids 14, S4 (2002)
Thomas, A. L. R., Taylor, G. K., Srygley, R. B., Nudds, R. L. & Bomphrey, R. J. Dragonfly flight: free-flight and tethered flow visualizations reveal a diverse array of unsteady lift-generating mechanisms, controlled primarily via angle of attack. J. Exp. Biol. 207, 4299–4323 (2004)
Bomphrey, R. J., Taylor, G. K. & Thomas, A. L. R. Smoke visualization of free-flying bumblebees indicates independent leading-edge vortices on each wing pair. Exp. Fluids 46, 811–821 (2009)
Srygley, R. B. & Thomas, A. L. R. Unconventional lift-generating mechanisms in free-flying butterflies. Nature 420, 660–664 (2002)
Videler, J. J., Stamhuis, E. J. & Povel, G. D. E. Leading-edge vortex lifts swifts. Science 306, 1960–1962 (2004)
Warrick, D. R., Tobalske, B. W. & Powers, D. R. Aerodynamics of the hovering hummingbird. Nature 435, 1094–1097 (2005)
Hedenström, A. et al. Bat flight generates complex aerodynamic tracks. Science 316, 894–897 (2007)
Nakata, T., Liu, H. & Bomphrey, R. J. A CFD-informed quasi-steady model of flapping wing aerodynamics. J. Fluid Mech. 783, 323–343 (2015)
Whitney, J. P. & Wood, R. J. Aeromechanics of passive rotation in flapping flight. J. Fluid Mech. 660, 197–220 (2010)
Ellington, C. P. The aerodynamics of hovering insect flight. V.A vortex theory. Phil. Trans. R. Soc. Lond. B 305, 115–144 (1984)
Dickinson, M. H., Lehmann, F.-O. & Sane, S. P. Wing rotation and the aerodynamic basis of insect flight. Science 284, 1954–1960 (1999)
Sane, S. P. & Dickinson, M. H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Exp. Biol. 205, 1087–1096 (2002)
Aono, H., Liang, F. & Liu, H. Near- and far-field aerodynamics in insect hovering flight: an integrated computational study. J. Exp. Biol. 211, 239–257 (2008)
Fry, S. N., Sayaman, R. & Dickinson, M. H. The aerodynamics of hovering flight in Drosophila. J. Exp. Biol. 208, 2303–2318 (2005)
Cator, L. J., Arthur, B. J., Harrington, L. C. & Hoy, R. R. Harmonic convergence in the love songs of the dengue vector mosquito. Science 323, 1077–1079 (2009)
Altshuler, D. L ., Dickson, W. B ., Vance, J. T ., Roberts, S. P & Dickinson, M. H. Short-amplitude high-frequency wing strokes determine the aerodynamics of honeybee flight. Proc. Natl Acad. Sci. USA 102, 18213–18218 (2005)
Willmott, A. P. & Ellington, C. P. The mechanics of flight in the hawkmoth Manduca sexta. I. Kinematics of hovering and forward flight. J. Exp. Biol. 200, 2705–2722 (1997)
Liu, H. Integrated modeling of insect flight: From morphology, kinematics to aerodynamics. J. Comput. Phys. 228, 439–459 (2009)
Vance, J. T. & Roberts, S. P. The effects of artificial wing wear on the flight capacity of the honey bee Apis mellifera. J. Insect Physiol. 65, 27–36 (2014)
Phillips, N., Knowles, K. & Bomphrey, R. J. The effect of aspect ratio on the leading-edge vortex over an insect-like flapping wing. Bioinspir. Biomim. 10, 056020 (2015)
Walker, S. M., Thomas, A. L. R. & Taylor, G. K. Photogrammetric reconstruction of high-resolution surface topographies and deformable wing kinematics of tethered locusts and free-flying hoverflies. J. R. Soc. Interface http://dx.doi.org/10.1098/rsif.2008.0245 (2009)
Walker, S. M., Thomas, A. L. R. & Taylor, G. K. Operation of the alula as an indicator of gear change in hoverflies. J. R. Soc. Interface http://dx.doi.org/10.1098/rsif.2011.0617 (2011)
Cheer, A. Y. L. & Koehl, M. A. R. Paddles and rakes: fluid-flow through bristled appendages of small organisms. J. Theor. Biol. 129, 17–39 (1987)
Nakata, T. & Liu, H. A fluid-structure interaction model of insect flight with flexible wings. J. Comput. Phys. 231, 1822–1847 (2012)
Berman, G. J. & Wang, Z. J. Energy-minimizing kinematics in hovering insect flight. J. Fluid Mech. 582, 153–168 (2007)
Acknowledgements
The authors were supported by the EPSRC (EP/H004025/1 and EP/M003698/1), BBSRC (BB/J001244/1). R.J.B. was supported by an EPSRC Career Acceleration Fellowship. S.M.W. was supported by a Royal Society University Research Fellowship. The work reported in this paper was funded by the Autonomous Systems Underpinning Research (ASUR) programme under the auspices of the Defence Science and Technology Laboratory (Dstl), UK Ministry of Defence. The authors acknowledge useful discussions with I. Russell and G. Gibson, P. Simoes for rearing the mosquitoes, and F. Albert-Davie and M. Inglis for assistance during raw data collection. The authors thank G. Taylor for the loan of four high-speed cameras purchased on European Research Council (ERC) grant 204513, and H. Liu for the permission to use the simulator and surface pressure distribution of the fruit fly wing.
Author information
Authors and Affiliations
Contributions
R.J.B. and S.M.W. conceived the experimental design; N.P. and S.M.W. designed and constructed the apparatus and N.P. led the data collection; all authors contributed to data collection; S.M.W. processed the raw data to extract detailed kinematics; T.N. performed the CFD simulations; N.P., T.N. and R.J.B. collected and processed the PIV data; R.J.B. drafted the manuscript; all authors contributed to data interpretation and manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks S. Swartz and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Extended data figures and tables
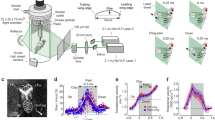
Extended Data Figure 1 Mosquito kinematics acquisition rig, wing lengths and mean kinematic patterns.
a, b, CAD representation (a) and photograph of the apparatus (b) used to record the body motion and wing kinematics of mosquitoes. The recording volume lies at the intersection of the fields of view of eight high-speed cameras, each creating a silhouette image of the mosquito by the shadow from high power IR-LED illumination. c, Wing-length estimates for mosquitoes captured in each of 15 sequences (M01-M15). Each estimate shows the median as a black line with shading representing the 95% confidence interval based upon all wingbeats from each sequence. Green and blue boxes group sequences that could not be reliably separated using Tukey’s honestly significant difference criterion, although they may come from different individuals of very similar size. As such, our fully processed data set of 15 sequences comprises between 12 and 15 individual mosquitoes. d, Mean wingbeat kinematics for all wingbeats in each of 15 recorded sequences. With reference to c, M01, M06 and M09, coloured green, may be from the same individual. Similarly, M05 and M11, coloured blue, may also be from a single individual.
Extended Data Figure 2 Wing surface pressure distribution and fluid flow visualized by streamlines showing consistency across each of the 15 mosquito sequences.
Each image corresponds to key instant t1. Formation of the trailing-edge vortex owing to capture of the induced flow from the preceding upstroke causes a distinct region of low pressure on the posterior portion of the wing.
Extended Data Figure 3 Wing surface pressure distribution and fluid flow visualized by streamlines showing consistency across each of the 15 mosquito sequences.
Each image corresponds to key instant t2. The downstroke force peak is dominated by a leading-edge vortex and corresponding low pressure on the anterior portion of the wing. The trailing-edge vortex has usually shed by this point in the stroke cycle.
Extended Data Figure 4 Wing surface pressure distribution and fluid flow visualized by streamlines showing consistency across each of the 15 mosquito sequences.
Each image corresponds to key instant t3. A low-pressure region is evident on the posterior portion of the wing caused by lift from rotational drag as the wing rotates around an axis close to the leading edge.
Extended Data Figure 5 Wing surface pressure distribution and fluid flow visualized by streamlines showing consistency across each of the 15 mosquito sequences.
Each image corresponds to key instant t4. Formation of a trailing-edge vortex on the aerodynamic upper, (anatomical ventral) surface of the wing during the upstroke due to capture of the induced flow from the preceding downstroke causes a distinct region of low pressure on the posterior portion of the wing.
Extended Data Figure 6 Wing surface pressure distribution and fluid flow visualized by streamlines showing consistency across each of the 15 mosquito sequences.
Each image corresponds to key instant t5. A low-pressure region exists over much of the aerodynamic upper, (anatomical ventral) surface of the wing as the result of a combination of rotational drag (caused by wing rotation around an axis close to the leading edge) and the remnants of the leading-edge vortex of the upstroke (which is no longer coherent in most examples but is retained in M03, M04, M06, M08, M11).
Extended Data Figure 7 Comparison of the local flow conditions at the trailing edge of the wings of mosquitoes and fruit flies during pronation (t/T = 0.09).
The comparatively higher local angle of attack of the mosquito wing is caused by the induced flow from the preceding upstroke. This is a product of kinematic tuning and a form of wake capture that leads to roll up of a transient, coherent, trailing-edge vortex. The vortex contributes to weight support along much of the length of the slender mosquito wing, despite it having little ground velocity during the rotational phase of the stroke cycle.
Extended Data Figure 8 Comparison of computed CFD lift force (black) compared against a simple quasi-steady model (grey) for each of 15 mosquito flight sequences.
Orange shading shows where the quasi-steady model over-predicts the force estimate from the CFD simulation, whereas green shows under-prediction. (See also Fig. 3)
Extended Data Figure 9 Lift and drag polars from high-fidelity CFD simulations of the mosquito wing model in continuous rotational sweep at four Reynolds numbers.
These were used to create dynamic lift coefficients for the blade element modelling with quasi-steady assumption. Coefficients are calculated for the third rotation, to account for the reduction in effective angle of attack when wings operate in the induced downwash from the preceding wing stroke.
Extended Data Figure 10 Morphology extraction and the CFD grid used for simulations.
a, b, We used the mean wing planform of three mosquitoes, extracted from microscope images of recently excised wings, to generate the wing grids used in our CFD simulations. c, d, The body shape was approximated from the silhouettes in the raw video data by fitting ellipses normal to the central axis of the body taken from each of the eight camera views. e, f, Local and background grids used for CFD. g, CFD grid and time-step independence was verified after performing simulations with variable cell density and time-step intervals.
Supplementary information
Wing stroke cycle
Video showing the experimental apparatus, raw data, wing geometry routine, kinematics, vortex wake (using isosurfaces of the Q-criterion), and pressure distribution and instantaneous flow fields at key instants (t1-t5) throughout the wing stroke cycle. (MOV 29036 kb)
Rights and permissions
About this article
Cite this article
Bomphrey, R., Nakata, T., Phillips, N. et al. Smart wing rotation and trailing-edge vortices enable high frequency mosquito flight. Nature 544, 92–95 (2017). https://doi.org/10.1038/nature21727
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature21727
This article is cited by
-
Bio-inspired Flapping Wing Aerodynamics: A Review
Journal of the Indian Institute of Science (2024)
-
Surfactants alter mosquito’s flight and physical condition
Scientific Reports (2023)
-
Investigate the Wake Flow on Houseflies with Particle-Tracking-Velocimetry and Schlieren Photography
Journal of Bionic Engineering (2023)
-
Novel flight style and light wings boost flight performance of tiny beetles
Nature (2022)
-
Physical models and vortex dynamics of swimming and flying: a review
Acta Mechanica (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.