Abstract
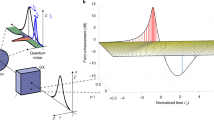
Squeezed states1,2,3,4 of electromagnetic radiation have quantum fluctuations below those of the vacuum field. They offer a unique resource for quantum information systems5 and precision metrology6, including gravitational wave detectors, which require unprecedented sensitivity7. Since the first experiments on this non-classical form of light8,9, quantum analysis has been based on homodyning techniques and photon correlation measurements10,11. These methods currently function in the visible to near-infrared and microwave12 spectral ranges. They require a well-defined carrier frequency, and photons contained in a quantum state need to be absorbed or amplified. Quantum non-demolition experiments13,14 may be performed to avoid the influence of a measurement in one quadrature, but this procedure comes at the expense of increased uncertainty in another quadrature. Here we generate mid-infrared time-locked patterns of squeezed vacuum noise. After propagation through free space, the quantum fluctuations of the electric field are studied in the time domain using electro-optic sampling with few-femtosecond laser pulses15,16. We directly compare the local noise amplitude to that of bare (that is, unperturbed) vacuum. Our nonlinear approach operates off resonance and, unlike homodyning or photon correlation techniques, without absorption or amplification of the field that is investigated. We find subcycle intervals with noise levels that are substantially less than the amplitude of the vacuum field. As a consequence, there are enhanced fluctuations in adjacent time intervals, owing to Heisenberg’s uncertainty principle, which indicate generation of highly correlated quantum radiation. Together with efforts in the far infrared17,18, this work enables the study of elementary quantum dynamics of light and matter in an energy range at the boundary between vacuum and thermal background conditions.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Stoler, D. Equivalence classes of minimum uncertainty packets. Phys. Rev. D 1, 3217–3219 (1970)
Hollenhorst, J. N. Quantum limits on resonant-mass gravitational-radiation detectors. Phys. Rev. D 19, 1669–1679 (1979)
Walls, D. F. Squeezed states of light. Nature 306, 141–146 (1983)
Loudon, R. & Knight, P. L. Squeezed light. J. Mod. Opt. 34, 709–759 (1987)
Braunstein, S. L. & van Loock, P. Quantum information with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005)
Caves, C. M. Quantum-mechanical noise in an interferometer. Phys. Rev. D 23, 1693–1708 (1981)
The LIGO Scientific Collaboration. Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light. Nat. Photon. 7, 613–619 (2013)
Slusher, R. E., Hollberg, L. W., Yurke, B., Mertz, J. C. & Valley, J. F. Observation of squeezed states generated by four-wave mixing in an optical cavity. Phys. Rev. Lett. 55, 2409–2412 (1985)
Wu, L.-A., Kimble, H. J., Hall, J. L. & Wu, H. Generation of squeezed states by parametric down conversion. Phys. Rev. Lett. 57, 2520–2523 (1986)
Altepeter, J. B., James, D. F. V. & Kwiat, P. G. in Quantum State Estimation (eds Paris, M. G. A. & Rˇehácˇek, J. ) 113–145 (Lecture Notes in Physics Vol. 649, Springer, 2004)
Lvovsky, A. I. & Raymer, M. G. Continuous-variable optical quantum-state tomography. Rev. Mod. Phys. 81, 299–332 (2009)
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013)
Levenson, M. D., Shelby, R. M., Reid, M. & Walls, D. F. Quantum nondemolition detection of optical quadrature amplitudes. Phys. Rev. Lett. 57, 2473–2476 (1986)
La Porta, A., Slusher, R. E. & Yurke, B. Back-action evading measurements of an optical field using parametric down conversion. Phys. Rev. Lett. 62, 28–31 (1989)
Riek, C. et al. Direct sampling of electric-field vacuum fluctuations. Science 350, 420–423 (2015)
Moskalenko, A. S., Riek, C., Seletskiy, D. V., Burkard, G. & Leitenstorfer, A. Paraxial theory of direct electro-optic sampling of the quantum vacuum. Phys. Rev. Lett. 115, 263601 (2015)
Esposito, M. et al. Photon number statistics uncover the fluctuations in non-equilibrium lattice dynamics. Nat. Commun. 6, 10249 (2015)
Benea-Chelmus, I.-C. et al. Subcycle measurement of intensity correlations in the terahertz frequency range. Phys. Rev. A 93, 043812 (2016)
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963)
Huber, R., Brodschelm, A., Tauser, F. & Leitenstorfer, A. Generation and field-resolved detection of femtosecond electromagnetic pulses tunable up to 41 THz. Appl. Phys. Lett. 76, 3191–3193 (2000)
Wasilewski, W., Lvovsky, A. I., Banaszek, K. & Radzewicz, C. Pulsed squeezed light: simultaneous squeezing of multiple modes. Phys. Rev. A 73, 063819 (2006)
Shaked, Y., Pomerantz, R., Vered, R. Z. & Pe’er, A. Observing the nonclassical nature of ultra-broadband bi-photons at ultrafast speed. New J. Phys. 16, 053012 (2014)
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987)
Lu, E. Y. C. Quantum correlations in two-photon amplification. Lett. Nuovo Cimento 3, 585–589 (1972)
Yablonovitch, E. Accelerating reference frame for electromagnetic waves in a rapidly growing plasma: Unruh–Davies–Fulling–DeWitt radiation and the nonadiabatic Casimir effect. Phys. Rev. Lett. 62, 1742–1745 (1989)
Smithey, D. T., Beck, M., Raymer, M. G. & Faridani, A. Measurement of the Wigner distribution and the density matrix of a light mode using optical homodyne tomography: applications to squeezed states and the vacuum. Phys. Rev. Lett. 70, 1244–1247 (1993)
Günter, G. et al. Sub-cycle switch-on of ultrastrong light–matter interaction. Nature 458, 178–181 (2009)
Kira, M., Koch, S. W., Smith, R. P., Hunter, A. E. & Cundiff, S. T. Quantum spectroscopy with Schrödinger-cat states. Nat. Phys. 7, 799–804 (2011)
Gallot, G. & Grischkowsky, D. Electro-optic detection of terahertz radiation. J. Opt. Soc. Am. B 16, 1204–1212 (1999)
Brida, D., Krauss, G., Sell, A. & Leitenstorfer, A. Ultrabroadband Er:fiber lasers. Laser Photonics Rev. 8, 409–428 (2014)
Adler, F., Sell, A., Sotier, F., Huber, R. & Leitenstorfer, A. Attosecond relative timing jitter and 13 fs tunable pulses from a two-branch Er:fiber laser. Opt. Lett. 32, 3504–3506 (2007)
Boyd, R. W. Nonlinear Optics 3rd edn, Chs 9, 11 (Academic Press, 2008)
Knight, P. & Allen, L. Concepts of Quantum Optics 71–72 (Pergamon Press, 1983)
Acknowledgements
We thank W. Belzig and D. Brida for discussions. Support by ERC Advanced Grant 290876 ‘UltraPhase’, by DFG via SFB767 and by NSF via a Postdoc Fellowship for D.V.S. (award number 1160764) is acknowledged.
Author information
Authors and Affiliations
Contributions
A.L. conceived the idea and wrote the first version of the paper. C.R., D.V.S. and A.L. designed the experiment. C.R., P.S., M.S. and D.V.S. performed the measurements and analysed the data. A.S.M. and G.B. worked out the theoretical description. All authors discussed the results and contributed to the writing of the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks M. Bellini, J. Faist, D. Fausti and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Figure 1 Sketch of the complete set-up underlying the experiments.
A mode-locked Er:fibre laser oscillator (Er:OSC) forms a train of femtosecond pulses at a repetition rate of 40 MHz (green). After a fibre-optic beam splitter, an electro-optic modulator (EOM) removes every second pulse in the pump branch (top), reducing the repetition rate to 20 MHz, and 12-fs pulses of centre wavelength λc = 1,550 nm are generated by an Er:doped-fibre amplifier (pump EDFA) with subsequent pulse compression (orange pulse train). A pulse energy Epump = 3.5 nJ is applied to pump the GaSe generation crystal (GX). The pulse train seeding the probe amplifier (probe EDFA) is left at a rate of 40 MHz and compressed to a duration of 5.8 fs and centre wavelength λc = 1,150 nm (blue pulse train). Eventually, a pulse energy of 120 pJ from this branch is available for probing the electro-optic effect in the AgGaS2 detector crystal (DX). Details on the laser technology are found in ref. 30. The NIR pump beam is focused into the GX by an off-axis parabolic mirror (sketched in yellow). A MIR electric field transient (red beam path) is generated by the second-order nonlinearity of the GX, collimated by another parabolic mirror and sent through a thin GaSb wafer acting as low-pass filter (LPF). This component is inserted at Brewster’s angle for minimum loss of the MIR field and complete suppression of the NIR pump. The probe pulse train travels over a variable optical delay stage (VD) to set the relative timing tD between pump and probe. It is reflected as s-polarized at a silicon beam combiner (BC), which is also inserted at Brewster’s angle with respect to the p-polarized MIR field. Both beams are focused to co-propagate inside the DX. The probe pulse train is then collimated by a final off-axis parabola and sent through an ellipsometer that consists of an achromatic quarter-wave plate (λ/4) and a Wollaston prism (WP). A balanced pair of photodiodes (BPD) detects a differential photocurrent, which is proportional to the MIR electric field amplitude that has been co-propagating with the probe. In total, only Eprobe = 80 pJ of probe pulse energy arrives at the BPD, owing to optical losses. Signals are demodulated at the Nyquist frequency of 20 MHz by a radio-frequency lock-in amplifier (RF lock-in) referenced to the EOM that picks every second pulse out of the pump pulse train. Signal collection and control of the VD are carried out by a personal computer (PC). An in-depth evaluation of the electro-optic sampling scheme is found in ref. 29.
Extended Data Figure 2 Explaining the concept of differential quantum sampling.
a, Lock-in demodulation scheme for obtaining coherent amplitude and RDN. Individual readout values for the differential photocurrent ΔI/I are sketched as a function of real time. The readouts carrying signal due to pumping of the GX are red and the sub-pulse train sampling bare vacuum input is shown in blue. The time interval of 25 ns between each probe pulse is given by the inverse of the probe repetition rate of 40 MHz. Demodulation of the coherent field amplitude EMIR is visualized in the top panel: the phase of the lock-in measurement at a reference frequency of 20 MHz is set such that the maximum difference between the average amplitude in the signal pulse train (red shading) and the reference pulse train (blue shading) is detected. Operating at the Nyquist frequency of the probe pulse train offers optimal performance in terms of amplitude and timing stability. Measurement of the RDN is illustrated in the bottom panel: we exploit two orthogonal readout phases at a reference frequency of 10 MHz to determine the level of fluctuations in the signal (red) and reference (blue) channels. In both cases, the standard deviation is computed; it corresponds to a convolution of the identical shot noise ΔESN in each channel and the noise due to the quantum fluctuations of the MIR electric field, which includes the pump-induced modulation of the quantum noise ΔErms in the signal channel and the bare vacuum noise ΔEvac in the reference channel. The sketch on the right-hand side corresponds to a delay time with strong anti-squeezing: here the r.m.s. width of the noise distribution in the signal channel (red) is larger than that of the reference noise (blue). This case would result in a positive value for the RDN. b, Individual readouts from the signal and reference channels. Raw data of a single scan over delay time tD from the two separate noise channels of the differential detection scheme, collected within 150 s. The blue curve results from the reference channel, which has a radio-frequency phase set such that only the standard deviation of electro-optic readouts ΔI/I with no pump pulse present in the generation crystal is probed at a reference frequency of 10 MHz (blue sub-pulse train and dashed line in a). Detecting only the bare vacuum input, this channel shows no dependence on the relative time delay tD between pumping and probing. In contrast, the channel with radio-frequency phase adjusted to sample the relative noise in the sub-pulse train that contains signals from the emitter excited by a pump pulse is plotted in red (noise signal, phase offset of 90° with respect to the reference channel; see red pulse train and line in a). Positions showing strong overshoot noise with respect to the vacuum reference are evident and indicate ‘anti-squeezing’, as sketched in an exaggerated way on the right-hand side of the bottom panel in a. But also delay times with the noise level of the red signal channel falling substantially below the blue reference data are clearly discernible, corresponding to ‘squeezing’ of the electric field with respect to the bare quantum vacuum. The data depicted in Figs 2 and 3 were processed in real time in the differential way described by equation (4) to obtain the RDN, subtracting any small variations that occur in the absolute noise floor of the laser or electro-optic detector. Statistics may be enhanced by averaging over multiple such scans.
Extended Data Figure 3 Radio-frequency noise spectrum of the electro-optic detector.
The relative noise spectral density at the output of the differential photodetector BPD, that is, at the input of the radio-frequency lock-in amplifier (see Extended Data Fig. 1), is shown. The black curve was recorded with the probe beam blocked and represents the electronic background (dark) noise of the system. The blue curve shows the noise spectrum under full illumination of the balanced photodiodes by the probe pulse train of repetition rate 40 MHz, but in the absence of any electro-optic signal input. The electronic low-pass filter is designed for a broad plateau of constant amplification and flat phase around the centre frequency of 10 MHz used for detection of the RDN (see Extended Data Fig. 2). The roll-off at a frequency of 20 MHz still leaves sufficient sensitivity for low-noise collection of the mean signal amplitudes, but results in a change in the radio-frequency phase angle with respect to the noise detection at 10 MHz, which needs to be adjusted correctly. The optical phase angle between the measured coherent field transients and the RDN patterns is not affected by this dispersion, because it results exclusively from scanning of the optical delay time tD. The red dashed line represents the relative shot-noise level calculated for a Poisson input of 5 × 108 photoelectrons generated per probe pulse. It demonstrates that the broad noise plateau around 10 MHz is dominated by the shot noise of the probe photon flux, ensuring independence of the RDN signal from the measurement bandwidth set by the lock-in amplifier. Strong suppression of the 40 MHz signal from the fundamental pulse train is evident from the small maximum in the blue curve and helps to ensure adequate linearity of the electronic system.
Extended Data Figure 4 Excluding nonlinearities in the readout electronics and technical noise of the coherent transients as potential spurious sources of RDN signals.
A universal check for any influence in the noise readout due to the presence of finite coherent field amplitudes is as follows. We exchange the roles of the two photodiodes at the input of the differential detector by rotating the Wollaston prism (WP) in the ellipsometer by an angle of 180° (see Extended Data Fig. 1). In this way, the polarity of the classical electric transients is inverted electronically but not physically (in contrast to Fig. 2, in which the pump polarization on the generation crystal has been rotated by 90°), resulting in the blue and red curves in the top panel. If the differential noise traces depicted in the bottom panel were artefacts due to some response of the electronic noise detection to either the amplitude or the slope of the mean readout, then we would expect those signals to also invert sign, but this is not the case. The high degree of agreement between the blue and red noise traces in the bottom panel, corresponding to the original and electronically inverted transients in the top panel, is a good indication of the linearity of our readout scheme. The result of this procedure implies that our noise traces must have an optical origin and that they do not result from any spurious processes in the readout electronics. The noise patterns in the bottom panel also cannot result from amplitude or phase noise of the coherent transients: in both cases, the periodicity of the noise would follow the second harmonic of the coherent transients and no negative signals with respect to bare vacuum noise would be expected.
Rights and permissions
About this article
Cite this article
Riek, C., Sulzer, P., Seeger, M. et al. Subcycle quantum electrodynamics. Nature 541, 376–379 (2017). https://doi.org/10.1038/nature21024
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature21024
This article is cited by
-
Discovery of ultrafast spontaneous spin switching in an antiferromagnet by femtosecond noise correlation spectroscopy
Nature Communications (2023)
-
Relativistic Bohmian trajectories of photons via weak measurements
Nature Communications (2022)
-
Detection of quantum-vacuum field correlations outside the light cone
Nature Communications (2022)
-
A six-octave optical frequency comb from a scalable few-cycle erbium fibre laser
Nature Photonics (2021)
-
Analysis of Subcycle Electro-Optic Sampling Without Background
Journal of Infrared, Millimeter, and Terahertz Waves (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.