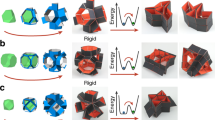
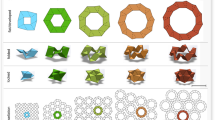
Abstract
Advances in fabrication technologies are enabling the production of architected materials with unprecedented properties. Most such materials are characterized by a fixed geometry, but in the design of some materials it is possible to incorporate internal mechanisms capable of reconfiguring their spatial architecture, and in this way to enable tunable functionality. Inspired by the structural diversity and foldability of the prismatic geometries that can be constructed using the snapology origami technique, here we introduce a robust design strategy based on space-filling tessellations of polyhedra to create three-dimensional reconfigurable materials comprising a periodic assembly of rigid plates and elastic hinges. Guided by numerical analysis and physical prototypes, we systematically explore the mobility of the designed structures and identify a wide range of qualitatively different deformations and internal rearrangements. Given that the underlying principles are scale-independent, our strategy can be applied to the design of the next generation of reconfigurable structures and materials, ranging from metre-scale transformable architectures to nanometre-scale tunable photonic systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
$29.99 / 30 days
cancel any time
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout






Similar content being viewed by others
References
Reis, P. M., Jaeger, H. M. & van Hecke, M. Designer matter: a perspective. Extreme Mech. Lett. 5, 25–29 (2015)
Sarrao, J. & Crabtree, G. Progress in mesoscale science. MRS Bull. 40, 919–922 (2015)
Christensen, J., Kadic, M., Kraft, O. & Wegener, M. Vibrant times for mechanical metamaterials. MRS Commun. 5, 453–462 (2015)
Pendry, J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000)
Smith, D. R., Pendry, J. B. & Wiltshire, M. C. K. Metamaterials and negative refractive index. Science 305, 788–792 (2004)
Lakes, R. Foam structures with a negative Poisson’s ratio. Science 235, 1038–1040 (1987)
Zheng, X. et al. Ultralight, ultrastiff mechanical metamaterials. Science 344, 1373–1377 (2014)
Meza, L. R., Das, S. & Greer, J. R. Strong, lightweight, and recoverable three-dimensional ceramic nanolattices. Science 345, 1322–1326 (2014)
Ergin, T., Stenger, N., Brenner, P., Pendry, J. B. & Wegener, M. Three-dimensional invisibility cloak at optical wavelengths. Science 328, 337–339 (2010)
Bückmann, T., Kadic, M., Schittny, R. & Wegener, M. Mechanical cloak design by direct lattice transformation. Proc. Natl Acad. Sci. USA 112, 4930–4934 (2015)
Miura, K. Method of Packaging and Deployment of Large Membranes in Space. Report No. 618, https://repository.exst.jaxa.jp/dspace/handle/a-is/7293 (Institute of Space and Astronautical Science, 1985)
Wei, Z. Y., Guo, Z. V., Dudte, L., Liang, H. Y. & Mahadevan, L. Geometric mechanics of periodic pleated origami. Phys. Rev. Lett. 110, 215501 (2013)
Schenk, M. & Guest, S. D. Geometry of miura-folded metamaterials. Proc. Natl Acad. Sci. USA 110, 3276–3281 (2013)
Silverberg, J. L. et al. Using origami design principles to fold reprogrammable mechanical metamaterials. Science 345, 647–650 (2014)
Lv, C., Krishnaraju, D., Konjevod, G., Yu, H. & Jiang, H. Origami based mechanical metamaterials. Sci. Rep. 4, 5979 (2014)
Waitukaitis, S., Menaut, R., Chen, B. G. & van Hecke, M. Origami multistability: from single vertices to metasheets. Phys. Rev. Lett. 114, 055503 (2015)
Dudte, L. H., Vouga, E., Tachi, T. & Mahadevan, L. Programming curvature using origami tessellations. Nat. Mater. 15, 583–588 (2016)
Silverberg, J. L. et al. Origami structures with a critical transition to bistability arising from hidden degrees of freedom. Nat. Mater. 14, 389–393 (2015)
Hawkes, E. et al. Programmable matter by folding. Proc. Natl Acad. Sci. USA 107, 12441–12445 (2010)
Tachi, T. & Miura, K. Rigid-foldable cylinders and cells. J. Int. Assoc. Shell Spat. Struct. 53, 217–226 (2012)
Filipov, E. T., Tachi, T. & Paulino, G. H. Origami tubes assembled into stiff, yet reconfigurable structures and metamaterials. Proc. Natl Acad. Sci. USA 112, 12321–12326 (2015)
Cheung, K. C., Tachi, T., Calisch, S. & Miura, K. Origami interleaved tube cellular materials. Smart Mater. Struct. 23, 094012 (2014)
Yasuda, H. & Yang, J. Re-entrant origami-based metamaterials with negative poisson’s ratio and bistability. Phys. Rev. Lett. 114, 185502 (2015)
Goldman, F. Using the snapology technique to teach convex polyhedra. In Origami Vol. 5 (eds Wang-Iverson, P., Lang, R. & Yim, M. ) 99–110 (CRC Press, 2011)
Strobl, H. Special Snapologyhttp://www.knotology.eu/PPP-Jena2010e/start.html (2010)
Overvelde, J. T. B. et al. A three-dimensional actuated origami-inspired transformable metamaterial with multiple degrees of freedom. Nat. Commun. 7, 10929 (2016)
Felton, S., Tolley, M., Demaine, E., Rus, D. & Wood, R. A method for building self-folding machines. Science 345, 644–646 (2014)
Andreini, A. Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative. Mem. Soc. Ital. Sci. 14, 75–129 (1907)
Pearce, P. & Pearce, S. Polyhedra Primer (Nostrand Reinhold, 1978)
Grunbaum, B. Uniform tilings of 3-space. Geombinatorics 4, 49–56 (1994)
Laliberté, T. & Gosselin, C. Construction, mobility analysis and synthesis of polyhedra with articulated faces. J. Mech. Robot. 6, 011007 (2013)
Bauer, J., Hengsbach, S., Tesari, I., Schwaiger, R. & Kraft, O. High-strength cellular ceramic composites with 3D microarchitecture. Proc. Natl Acad. Sci. USA 111, 2453–2458 (2014)
Meza, L. R. et al. Resilient 3D hierarchical architected metamaterials. Proc. Natl Acad. Sci. USA 112, 11502–11507 (2015)
Leong, T. G. et al. Tetherless thermobiochemically actuated microgrippers. Proc. Natl Acad. Sci. USA 106, 703–708 (2009)
Liu, Y., Boyles, J. K., Genzer, J. & Dickey, M. D. Self-folding of polymer sheets using local light absorption. Soft Matter 8, 1764–1769 (2012)
Laflin, K. E., Morris, C. J., Muqeem, T. & Gracias, D. H. Laser triggered sequential folding of microstructures. Appl. Phys. Lett. 101, 131901 (2012)
Shenoy, V. B. & Gracias, D. H. Self-folding thin-film materials: from nanopolyhedra to graphene origami. MRS Bull. 37, 847–854 (2012)
Cho, J. H. et al. Nanoscale origami for 3D optics. Small 7, 1943–1948 (2011)
Xu, S. et al. Assembly of micro/nanomaterials into complex, three-dimensional architectures by compressive buckling. Science 347, 154–159 (2015)
Kim, J., Hanna, J. A., Byun, M., Santangelo, C. D. & Hayward, R. C. Designing responsive buckled surfaces by halftone gel lithography. Science 335, 1201–1205 (2012)
Acknowledgements
This work was supported by the Materials Research Science and Engineering Center under NSF Award number DMR-1420570. K.B. also acknowledges support from the National Science Foundation (CMMI-1149456-CAREER). We thank M. Mixe and S. Shuham for assistance in the fabrication of the cardboard prototypes, and R. Wood for the use of his laboratory.
Author information
Authors and Affiliations
Contributions
J.T.B.O., C.H. and K.B. proposed and designed the research; J.T.B.O. performed the numerical calculations; J.T.B.O., C.H. and J.C.W. designed and fabricated the models; J.T.B.O. performed the experiments; J.T.B.O. and K.B. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks J. Paik, D. Pasini and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, which Includes Supplementary Methods, a Supplementary Discussion, Supplementary Figures 1-12, Supplementary Table 1 and additional references. The fabrication approaches used to make the cardboard prototypes and 3D printed prototypes are described. Also described are the numerical algorithm that were implemented in Matlab (i) to predict the number of degrees of freedom and corresponding deformation modes of 3D prismatic architected materials with rigid faces, and (ii) to characterize the elastic response of 3D prismatic architected materials with deformable faces. (PDF 40377 kb)
Supplementary Data
This zipped file contains the Matlab code used to generate the prismatic architected materials and determine their mobility and deformation modes. A detailed description of the code is given in the Supplementary Information. (ZIP 33 kb)
Strategy to design prismatic architected materials
Space-filling and periodic assemblies of convex polyhedra are used as a template to construct prismatic architected materials. After selecting a space-filling tessellation, we focus on a unit cell and separate the polyhedra while ensuring that the normals of all periodically-placed face pairs remain aligned. We then extrude the edges of the polyhedra in the direction normal to their faces to construct the extruded unit cell, which is then used to form the architected material. (MP4 1670 kb)
Reconfigurability of prismatic architected materials
Three prototypes of the 3D prismatic architected materials were constructed using cardboard for the rigid faces and double-sided tape for flexible hinges. Depending on the space-filling assembly of polyhedra used as a template, the resulting architected material has different deformation modes or is completely rigid. (MP4 10101 kb)
Enhancing the reconfigurability of prismatic architected materials.
To alter the reconfigurability of the architected materials, we reduce their connectivity by extruding only selected face pairs of the unit cell, while making the remaining faces rigid. As an example, the architected material based on the space-filling assembly of truncated octahedra can made reconfigurable by extruding only 6 of its faces and making the remaining 8 faces rigid. (MP4 9512 kb)
Different modes observed in prismatic architected materials.
A variety of qualitatively different deformation modes can be achieved in the proposed prismatic architected materials besides shear, including internal reconfigurations that do not alter the macroscopic shape of the materials, and uniform expansion along one or two principal directions. (MP4 8025 kb)
3D printed reconfigurable architected materials.
Using multi-material additive manufacturing we fabricated two of the proposed prismatic architected materials. The faces were fabricated using a rigid material, while the hinges were given a finite size and printed using a softer material. The two architectures that were printed are characterized by respectively zero and one deformation modes. (MP4 7133 kb)
Rights and permissions
About this article
Cite this article
Overvelde, J., Weaver, J., Hoberman, C. et al. Rational design of reconfigurable prismatic architected materials. Nature 541, 347–352 (2017). https://doi.org/10.1038/nature20824
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature20824
This article is cited by
-
Electrothermally controlled origami fabricated by 4D printing of continuous fiber-reinforced composites
Nature Communications (2024)
-
Obtaining auxetic and isotropic metamaterials in counterintuitive design spaces: an automated optimization approach and experimental characterization
npj Computational Materials (2024)
-
Zero modes activation to reconcile floppiness, rigidity, and multistability into an all-in-one class of reprogrammable metamaterials
Nature Communications (2024)
-
Hydrogel muscles powering reconfigurable micro-metastructures with wide-spectrum programmability
Nature Materials (2023)
-
Approximating complex 3D curves using origami spring structures
Communications Engineering (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.