Abstract
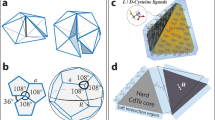
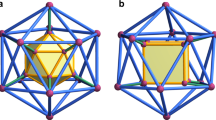
Rational control of the self-assembly of large structures is one of the key challenges in chemistry1,2,3,4,5,6,7,8,9, and is believed to become increasingly difficult and ultimately impossible as the number of components involved increases. So far, it has not been possible to design a self-assembled discrete molecule made up of more than 100 components. Such molecules—for example, spherical virus capsids10—are prevalent in nature, which suggests that the difficulty in designing these very large self-assembled molecules is due to a lack of understanding of the underlying design principles. For example, the targeted assembly of a series of large spherical structures containing up to 30 palladium ions coordinated by up to 60 bent organic ligands11,12,13,14,15,16 was achieved by considering their topologies17. Here we report the self-assembly of a spherical structure that also contains 30 palladium ions and 60 bent ligands, but belongs to a shape family that has not previously been observed experimentally17. The new structure consists of a combination of 8 triangles and 24 squares, and has the symmetry of a tetravalent Goldberg polyhedron18,19. Platonic and Archimedean solids have previously been prepared through self-assembly, as have trivalent Goldberg polyhedra, which occur naturally in the form of virus capsids20 and fullerenes21. But tetravalent Goldberg polyhedra have not previously been reported at the molecular level, although their topologies have been predicted using graph theory. We use graph theory to predict the self-assembly of even larger tetravalent Goldberg polyhedra, which should be more stable, enabling another member of this polyhedron family to be assembled from 144 components: 48 palladium ions and 96 bent ligands.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Conn, M. M. & Rebek, J. Self-assembling capsules. Chem. Rev. 97, 1647–1668 (1997)
Caulder, D. L. & Raymond, K. N. Supermolecules by design. Acc. Chem. Res. 32, 975–982 (1999)
Saalfrank, R. W., Maid, H. & Scheurer, A. Supramolecular coordination chemistry: the synergistic effect of serendipity and rational design. Angew. Chem. Int. Ed. 47, 8794–8824 (2008)
Forgan, R. S., Sauvage, J.-P. & Stoddart, J. F. Chemical topology: complex molecular knots, links, and entanglements. Chem. Rev. 111, 5434–5464 (2011)
Chakrabarty, R., Mukherjee, P. S. & Stang, P. J. Supramolecular coordination: self-assembly of finite two- and three-dimensional ensembles. Chem. Rev. 111, 6810–6918 (2011)
Young, N. J. & Hay, B. P. Structural design principles for self-assembled coordination polygons and polyhedra. Chem. Commun. 49, 1354–1379 (2013)
Smulders, M. M. J., Riddell, I. A., Browne, C. & Nitschke, J. R. Building on architectural principles for three-dimensional metallosupramolecular construction. Chem. Soc. Rev. 42, 1728–1754 (2013)
Cook, T. R. & Stang, P. J. Recent developments in the preparation and chemistry of metallacycles and metallacages via coordination. Chem. Rev. 115, 7001–7045 (2015)
Hsia, Y. et al. Design of a hyperstable 60-subunit protein icosahedron. Nature 535, 136–139 (2016)
Zlotnick, A. To build a virus capsid: an equilibrium model of the self assembly of polyhedral protein complexes. J. Mol. Biol. 241, 59–67 (1994)
Harris, K., Fujita, D. & Fujita, M. Giant hollow MnL2n spherical complexes: structure, functionalisation and applications. Chem. Commun. 49, 6703–6712 (2013)
Fujita, D., Yokoyama, H., Ueda, Y., Sato, S. & Fujita, M. Geometrically restricted intermediates in the self-assembly of an M12L24 cuboctahedral complex. Angew. Chem. Int. Ed. 54, 155–158 (2015)
Suzuki, K., Tominaga, M., Kawano, M. & Fujita, M. Self-assembly of an M6L12 coordination cube. Chem. Commun. 1638–1640 (2009)
Tominaga, M. et al. Finite, spherical coordination networks that self-organize from 36 small components. Angew. Chem. Int. Ed. 43, 5621–5625 (2004)
Sun, Q. F. et al. Self-assembled M24L48 polyhedra and their sharp structural switch upon subtle ligand variation. Science 328, 1144–1147 (2010)
Fujita, D. et al. Self-assembly of M30L60 icosidodecahedron. Chem 1, 91–101 (2016)
Coxeter, H. S. M. Introduction to Geometry 2nd edn, Ch. 10, 21 (Wiley, 1989)
Goldberg, M. A class of multi-symmetric polyhedra. Tohoku Math. J. 43, 104–108 (1937)
Schein, S. & Gayed, J. M. Fourth class of convex equilateral polyhedron with polyhedral symmetry related to fullerenes and viruses. Proc. Natl Acad. Sci. USA 111, 2920–2925 (2014)
Caspar, D. L. D. & Klug, A. Physical principles in the construction of regular viruses. Cold Spring Harb. Symp. Quant. Biol. 27, 1–24 (1962)
Fowler, P. W. & Manolopoulos, D. E. An Atlas of Fullerenes Ch. 2 (Courier Corporation, 2006)
Bunzen, M. et al. Self-assembly of M24L48 polyhedra based on empirical prediction. Angew. Chem. Int. Ed. 51, 3161–3163 (2012)
Takata, M. The MEM/Rietveld method with nano-applications — accurate charge-density studies of nano-structured materials by synchrotron-radiation powder diffraction. Acta Crystallogr. A 64, 232–245 (2008)
Fujita, D. et al. Protein encapsulation within synthetic molecular hosts. Nat. Commun. 3, 1093 (2012)
Prasad, B. V. & Schmid, M. F. Principles of virus structural organization. Adv. Exp. Med. Biol. 726, 17–47 (2012)
Sikirić, M. D. & Deza, M. in The Mathematics and Topology of Fullerenes (eds Cataldo, F. et al.) Ch. 6, 103–116 (Springer, 2011)
Dutour, M. & Deza, M. Goldberg–Coxeter construction for 3- and 4-valent plane graphs. Electron. J. Combin. 11, R20 (2004)
Brinkmann, G. & Deza, M. Lists of face-regular polyhedra. J. Chem. Inf. Comput. Sci. 40, 530–541 (2000)
Zhou, Z. & Harris, K. D. M. Design of a molecular quasicrystal. ChemPhysChem 7, 1649–1653 (2006)
Vekilov, Y. K. & Chernikov, M. A. Quasicrystals. Phys. Uspekhi 53, 537–560 (2010)
Kabsch, W. XDS. Acta Crystallogr. D 66, 125–132 (2010)
Sheldrick, G. M. SHELXT — integrated space-group and crystal-structure determination. Acta Crystallogr. A 71, 3–8 (2015)
Sheldrick, G. M. Crystal structure refinement with SHELXL. Acta Crystallogr. C 71, 3–8 (2015)
Tanaka, H. et al. ENIGMA: maximum-entropy method program package for huge systems. J. Appl. Cryst. 35, 282–286 (2002)
Schwerdtfeger, P., Wirz, L. N. & Avery, J. The topology of fullerenes. WIREs Comp. Mol. Sci. 5, 96–145 (2015)
Yokoyama, H., Ueda, Y., Fujita, D., Sato, S. & Fujita, M. Finely resolved threshold for the Sharp M12L24/M24L48 structural switch in multi-component MnL2n polyhedral assemblies: X-ray, MS, NMR, and ultracentrifugation analyses. Chem. Asian J. 10, 2292–2295 (2015)
Acknowledgements
This work was supported by the JST–PRESTO programme and the ACCEL programme, and partly supported by KAKENHI (25102007). The synchrotron X-ray crystallography was performed at the BL38B1 and BL41XU beamlines at SPring-8 (2014A0042 and 2015B0120); preliminarily experiments were performed at the BL-1A beamline at KEK PF (2015G097). We thank M. Kotani and M. Tagami for providing us with mathematical discussion (see Methods) and references (refs 26, 27, 28).
Author information
Authors and Affiliations
Contributions
D.F. and Y.U. performed and analysed the experiments. D.F. and S.S. worked on the preliminary X-ray diffraction analysis. N.M. and T.K. finalized the X-ray data. D.F. built the mathematical discussion. D.F. and M.F. wrote the paper. D.F. and M.F. designed and supervised the research project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Additional information
Reviewer Information Nature thanks F. Beuerle, P. Schwerdtfeger and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Extended data figures and tables
Extended Data Figure 1 NMR study of the self-assembly of ligand 1.
a, 1H NMR spectrum (500 MHz, DMSO-d6, 300 K) of ligand 1. The signal denoted PyHα is derived from the protons in the pydridyl α-position; that denoted PyHβ is derived from the protons in the pyridyl β-position. The signal denoted –OCH3 is from the methoxy protons. b, 1H NMR spectrum of 1 after self-assembly with palladium(ii) ions (BF4− salt). The aromatic signals are shifted downfield and heavily broadened. c, 1H DOSY spectrum of 1 after self-assembly with palladium(ii) ions (BF4− salt). The spectrum indicates a single product with a diffusion coefficient D of 2.6 × 10−11 m2 s−1 (logD = −10.58). The grey band is a guide to the eye. All of the NMR spectra (500 MHz) were measured for DMSO-d6 solutions at 300 K.
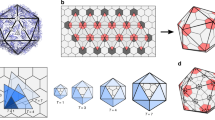
Extended Data Figure 2 Schematic representation of larger tet-G(h, k) polyhedra.
Polyhedra with the topology of tet-G(3, 0) (or, equivalently of tet-G(0, 3); Q = 9), tet-G(1, 3) (Q = 10) or tet-G(2, 3) (Q = 13). For Q = 9 and Q = 10, the other structure in the chiral pair (tet-G(3, 1) and tet-G(3, 2), respectively) is a mirror image of the polyhedron shown.
Extended Data Figure 3 1H NMR of ligand 1.
Full range spectrum: 500 MHz, CDCl3, 27 °C.
Extended Data Figure 4 13C NMR of ligand 1.
Full range spectrum: 125 MHz, CDCl3, 27 °C.
Extended Data Figure 5 1H NMR of 3.
Full range spectrum: 500 MHz, DMSO-d6, 27 °C.
Extended Data Figure 6 1H NMR of 3.
Full range spectrum: 500 MHz, DMF-d5, 27 °C.
Extended Data Figure 7 1H DOSY NMR of 3.
Full range spectrum: 500 MHz, DMSO-d6, 27 °C. For comparison with M12L24 or M24L48 complexes, see ref. 36.
Extended Data Figure 8 1H DOSY NMR of 3.
Full range spectrum: 500 MHz, DMF-d5, 27 °C. For comparison with M12L24 or M24L48 complexes, see ref. 36.
Supplementary information
Supplementary Data 1
X-ray data of M30L60. (CIF 13745 kb)
Supplementary Data 2
X-ray data of M48L96. (CIF 1216 kb)
MEM electron density map of M30L6.
360° rotating movie of the electron density map. (MOV 52204 kb)
MEM electron density map of M48L96.
360° rotating movie of the electron density map. (MOV 48346 kb)
Rights and permissions
About this article
Cite this article
Fujita, D., Ueda, Y., Sato, S. et al. Self-assembly of tetravalent Goldberg polyhedra from 144 small components. Nature 540, 563–566 (2016). https://doi.org/10.1038/nature20771
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature20771
This article is cited by
-
Non-statistical assembly of multicomponent [Pd2ABCD] cages
Nature Chemistry (2024)
-
Systematic construction of progressively larger capsules from a fivefold linking pyrrole-based subcomponent
Nature Synthesis (2023)
-
The sharp structural switch of covalent cages mediated by subtle variation of directing groups
Nature Communications (2023)
-
Kinetic trapping of 2,4,6-tris(4-pyridyl)benzene and ZnI2 into M12L8 poly-[n]-catenanes using solution and solid-state processes
Scientific Reports (2023)
-
[2,2] Paracyclophanes-based double helicates for constructing artificial light-harvesting systems and white LED device
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.