Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Progressive incision of the Channeled Scablands by outburst floods

Nature volume 538, pages 229–232 (2016)Cite this article

Subjects

Abstract

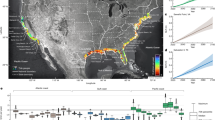
The surfaces of Earth and Mars contain large bedrock canyons that were carved by catastrophic outburst floods1,2. Reconstructing the magnitude of these canyon-forming floods is essential for understanding the ways in which floods modify planetary surfaces1,2, the hydrology of early Mars3 and abrupt changes in climate4. Flood discharges are often estimated by assuming that the floods filled the canyons to their brims with water; however, an alternative hypothesis is that canyon morphology adjusts during incision such that bed shear stresses exceed the threshold for erosion by a small amount5. Here we show that accounting for erosion thresholds during canyon incision results in near-constant discharges that are five- to ten-fold smaller than full-to-the-brim estimates for Moses Coulee, a canyon in the Channeled Scablands, which was carved during the Pleistocene by the catastrophic Missoula floods in eastern Washington, USA. The predicted discharges are consistent with flow-depth indicators from gravel bars within the canyon. In contrast, under the assumption that floods filled canyons to their brims, a large and monotonic increase in flood discharge is predicted as the canyon was progressively incised, which is at odds with the discharges expected for floods originating from glacial lake outbursts. These findings suggest that flood-carved landscapes in fractured rock might evolve to a threshold state for bedrock erosion, thus implying much lower flood discharges than previously thought.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: The Moses Coulee study site.
Figure 2: Depositional landforms in Moses Coulee.
Figure 3: Simulated discharge and water depths.
Figure 4: Co-evolution of topography and flood level predicted by the brim-full and threshold shear stress models.

Similar content being viewed by others

References

  1. Bretz, J. H. The Channeled Scablands of the Columbia Plateau. J. Geol. 31, 617–649 (1923)

    Article  ADS  Google Scholar 

  2. Baker, V. R. The Channels of Mars (Univ. Texas Press, 1982)

  3. Carr, M. H. Mars: a water-rich planet? Icarus 68, 187–216 (1986)

    Article  CAS  ADS  Google Scholar 

  4. Barber, D. et al. Forcing of the cold event of 8,200 years ago by catastrophic drainage of Laurentide lakes. Nature 400, 344–348 (1999)

    Article  CAS  ADS  Google Scholar 

  5. Lamb, M. P. & Fonstad, M. A. Rapid formation of a modern bedrock canyon by a single flood event. Nat. Geosci. 3, 477–481 (2010)

    Article  CAS  ADS  Google Scholar 

  6. Bretz, J. H. The Lake Missoula floods and the Channeled Scabland. J. Geol. 77, 505–543 (1969)

    Article  ADS  Google Scholar 

  7. O’Connor, J. E., Grant, G. E. & Costa, J. E. in Ancient Floods, Modern Hazards: Principles and Applications of Paleoflood Hydrology (eds House, P. K. et al.) 359–385 (American Geophysical Union, 2002)

  8. Baker, V. et al. Ancient oceans, ice sheets and the hydrological cycle on Mars. Nature 352, 589–594 (1991)

    Article  ADS  Google Scholar 

  9. Baynes, E. R. et al. Erosion during extreme flood events dominates Holocene canyon evolution in northeast Iceland. Proc. Natl Acad. Sci. USA 112, 2355–2360 (2015)

    Article  CAS  ADS  Google Scholar 

  10. Carr, M. H. Formation of Martian flood features by release of water from confined aquifers. J. Geophys. Res. Solid Earth 84, 2995–3007 (1979)

    Article  Google Scholar 

  11. Baker, V. R. Paleohydrology and Sedimentology of Lake Missoula Flooding in Eastern Washington. GSA Special Paper 144 (Geological Society of America, 1973)

  12. Denlinger, R. & O’Connell, D. Simulations of cataclysmic outburst floods from Pleistocene Glacial Lake Missoula. Geol. Soc. Am. Bull. 122, 678–689 (2010)

    Article  ADS  Google Scholar 

  13. O’Connor, J. E. & Baker, V. R. Magnitudes and implications of peak discharges from glacial Lake Missoula. Geol. Soc. Am. Bull. 104, 267–279 (1992)

    Article  ADS  Google Scholar 

  14. Komar, P. D. Comparisons of the hydraulics of water flows in Martian outflow channels with flows of similar scale on Earth. Icarus 37, 156–181 (1979)

    Article  ADS  Google Scholar 

  15. Miyamoto, H. et al. Cataclysmic Scabland flooding: insights from a simple depth-averaged numerical model. Environ. Model. Softw. 22, 1400–1408 (2007)

    Article  Google Scholar 

  16. Lamb, M. P., Mackey, B. H. & Farley, K. A. Amphitheater-headed canyons formed by megaflooding at Malad Gorge, Idaho. Proc. Natl Acad. Sci. USA 111, 57–62 (2014)

    Article  CAS  ADS  Google Scholar 

  17. Lamb, M. P., Dietrich, W. E., Aciego, S. M., DePaolo, D. J. & Manga, M. Formation of Box Canyon, Idaho, by megaflood: implications for seepage erosion on Earth and Mars. Science 320, 1067–1070 (2008)

    Article  CAS  ADS  Google Scholar 

  18. Anton, L., Mather, A., Stokes, M., Muñoz-Martin, A. & De Vicente, G. Exceptional river gorge formation from unexceptional floods. Nat. Commun. 6, 7963 (2015)

    Article  CAS  ADS  Google Scholar 

  19. Coleman, N. M. Hydrographs of a Martian flood from a breached crater lake, with insights about flow calculations, channel erosion rates, and chasma growth. J. Geophys. Res. Planets 118, 263–277 (2013)

    Article  ADS  Google Scholar 

  20. Warner, N., Gupta, S., Muller, J., Kim, J. & Lin, S. A refined chronology of catastrophic outflow events in Ares Vallis, Mars. Earth Planet. Sci. Lett. 288, 58–69 (2009)

    Article  CAS  ADS  Google Scholar 

  21. Lamb, M. P., Finnegan, N. J., Scheingross, J. S. & Sklar, L. S. New insights into the mechanics of fluvial bedrock erosion through flume experiments and theory. Geomorphology 244, 33–55 (2015)

    Article  ADS  Google Scholar 

  22. Lamb, M. P. & Dietrich, W. E. The persistence of waterfalls in fractured rock. Geol. Soc. Am. Bull. 121, 1123–1134 (2009)

    Article  ADS  Google Scholar 

  23. Lapotre, M. G. A., Lamb, M. P. & Williams, R. M. E. Canyon formation constraints on the discharge of catastrophic outburst floods of Earth and Mars. J. Geophys. Res. Planets 121, 1232–1263 (2016)

    Article  ADS  Google Scholar 

  24. Waitt, R. B. Case for periodic, colossal jökulhlaups from Pleistocene glacial Lake Missoula. Geol. Soc. Am. Bull. 96, 1271–1286 (1985)

    Article  ADS  Google Scholar 

  25. Parker, G. Self-formed straight rivers with equilibrium banks and mobile bed. Part 2. The gravel river. J. Fluid Mech. 89, 127–146 (1978)

    Article  ADS  Google Scholar 

  26. Wohl, E. E. Bedrock benches and boulder bars: floods in the Burdekin Gorge of Australia. Geol. Soc. Am. Bull. 104, 770–778 (1992)

    Article  ADS  Google Scholar 

  27. Schmidt, J. C., Grams, P. E. & Leschin, M. F. in The Controlled Flood in Grand Canyon (eds Webb, R. H. et al.) 185–203 (American Geophysical Union, 1999)

  28. Church, M. Bed material transport and the morphology of alluvial river channels. Annu. Rev. Earth Planet. Sci. 34, 325–354 (2006)

    Article  CAS  ADS  Google Scholar 

  29. Venditti, J. G. et al. Flow in bedrock canyons. Nature 513, 534–537 (2014)

    Article  CAS  ADS  Google Scholar 

  30. Andrews-Hanna, J. C. & Phillips, R. J. Hydrological modeling of outflow channels and chaos regions on Mars. J. Geophys. Res. Planets 112, E08001 (2007)

    Article  ADS  Google Scholar 

  31. Roberts, S. G., Nielsen, O. M. & Jakeman, J. in Modeling, Simulation and Optimization of Complex Processes (eds Bock, H.G. et al.) 489–498 (Springer, 2008)

  32. Roberts, S., Nielsen, O., Gray, D., Sexton, J. & Davies, G. ANUGA User Manual. Release 2.0. https://github.com/GeoscienceAustralia/anuga_core/raw/master/doc/anuga_user_manual.pdf (2015)

  33. Parker, G. Selective sorting and abrasion of river gravel. II: applications. J. Hydraul. Eng. 117, 150–171 (1991)

    Article  Google Scholar 

  34. Johnson, J. P. A surface roughness model for predicting alluvial cover and bed load transport rate in bedrock channels. J. Geophys. Res. Earth Surface 119, 2147–2173 (2014)

    Article  ADS  Google Scholar 

  35. Dubinski, I. M. & Wohl, E. Relationships between block quarrying, bed shear stress, and stream power: a physical model of block quarrying of a jointed bedrock channel. Geomorphology 180–181, 66–81 (2013)

    Article  ADS  Google Scholar 

  36. Selby, M. J. Hillslope Materials and Processes 93 (Oxford Univ. Press, 1993)

  37. Long, P. E. & Wood, B. J. Structures, textures, and cooling histories of Columbia River basalt flows. Geol. Soc. Am. Bull. 97, 1144–1155 (1986)

    Article  ADS  Google Scholar 

  38. Schultz, R. Limits on strength and deformation properties of jointed basaltic rock masses. Rock Mech. Rock Eng. 28, 1–15 (1995)

    Article  ADS  Google Scholar 

  39. Ehlmann, B. L., Viles, H. A. & Bourke, M. C. Quantitative morphologic analysis of boulder shape and surface texture to infer environmental history: a case study of rock breakdown at the Ephrata Fan, Channeled Scabland, Washington. J. Geophys. Res. Earth Surface 113, F02012 (2008)

    Article  ADS  Google Scholar 

  40. NiÑo, Y., Lopez, F. & Garcia, M. Threshold for particle entrainment into suspension. Sedimentology 50, 247–263 (2003)

    Article  ADS  Google Scholar 

  41. Ferguson, R. & Church, M. A simple universal equation for grain settling velocity. J. Sediment. Res. 74, 933–937 (2004)

    Article  ADS  Google Scholar 

Download references

Acknowledgements

This research was supported by a Caltech Texaco Prize Postdoctoral Fellowship, collaborative NSF (1529528, 1529110) funding to I.J.L. and M.P.L., and a NASA (NNX13AM83G) award to M.P.L. We thank E. Simon, M. Lapotre and S. Roberts for assistance and advice with the hydraulic modelling, and participants in the Caltech field methods course for field assistance.

Author information

Authors and Affiliations

  1. Department of Geosciences, University of Massachusetts, Amherst, 01003, Massachusetts, USA

    Isaac J. Larsen

  2. Division of Geological and Planetary Sciences, California Institute of Technology, Pasadena, 91125, California, USA

    Isaac J. Larsen & Michael P. Lamb

Authors
  1. Isaac J. Larsen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael P. Lamb
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

I.J.L. and M.P.L. designed the study and wrote the manuscript. I.J.L. conducted the hydraulic simulations.

Corresponding author

Correspondence to Isaac J. Larsen.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Additional information

Reviewer Information Nature thanks J. Venditti and the other anonymous reviewer(s) for their contribution to the peer review of this work.

Extended data figures and tables

Extended Data Figure 1 Computational mesh resolution.

a, Map of the computational domain (green outline). Black square shows the location of b. b, Map showing the different triangular mesh resolutions within the computational domain, with a maximum triangle area of 900 m2 within the white polygon in a and 5,000 m2 throughout the rest of the domain. We used a smaller triangle area in the study reach (within the white polygon) to better resolve spatial variability in shear stresses and a slightly larger triangle area elsewhere for computational efficiency.

Extended Data Figure 2 Hillshade maps of the study reach for each bed elevation.

These maps depict the reconstructed topography in Moses Coulee, which is based on the elevation of terraces and the modern channel bed upstream from the knickzone. a, b, Bed elevation D; c, d, bed elevation C; e, f, bed elevation B; g, h, bed elevation A; i, j, modern topography.

Extended Data Figure 3 Bed shear stress as a function of discharge for sites on the Moses Coulee knickzone.

Data correspond to locations shown in Extended Data Fig. 7. For nearly all simulated discharges, the modelled shear stresses on the knickzone exceed the thresholds for plucking via block sliding, indicating that the knickzone would probably have been rapidly eroding during floods or that it is made up of stronger rock.

Extended Data Figure 4 Flood depth versus time for a typical simulation.

The example shown is a flood with a discharge of 106 m3 s−1 routed through the modern topography. The grey box shows the final ten time-steps, from which the model results (stage, velocity, shear stress and so on) were extracted and used to produce time-averaged grids to reduce the influence of transient waves relative to data from a single time-step.

Extended Data Figure 5 Cumulative bed stress probability density functions.

The light grey bar shows the lower (467 Pa) and upper (751 Pa) threshold shear stress bounds for plucking of 0.5-m blocks. The dark grey bar shows the threshold stress bounds (117 Pa and 1,242 Pa) assuming a wider distribution of block sizes of 0.13–0.83 m, based on the D16 and D84 (16th and 84th percentiles) of basalt clasts at the Ephrata Fan and Drumheller Channels sites, respectively (Extended Data Fig. 6). Cumulative probability density functions are shown for the brim-full flood (discharge of 3.0 × 106 m3 s−1; black line) and the lower (0.3 × 106 m3 s−1; red line) and upper (0.6 × 106 m3 s−1; blue line) flood discharge bounds predicted by the threshold shear stress model for the modern Moses Coulee topography. Data are extracted from each grid cell within the entire length of Moses Coulee (Fig. 1b). For the brim-full flood, only 8% of the terrain of Moses Coulee has modelled bed shear stresses within the bounds for plucking 0.5-m blocks, and this increases to 33% when considering the wider range of block sizes; some areas have extremely high bed stresses of more than 10,000 Pa. In contrast, for discharges predicted by the threshold shear stress model, 25% of the terrain has shear stresses within the bounds for plucking 0.5-m blocks, and this increases to 67% when considering a wider distribution of block sizes. This high proportion of bed stresses within the plucking threshold range, relative to the brim-full flood, is consistent with the hypothesis that the channel adjusts so that a large portion of the terrain is near the threshold state during megaflood incision. Note that the study locations in Extended Data Fig. 7 were used to define the discharge bounds for the threshold shear stress model, so all of those locations have bed stresses within the plucking threshold range by definition (see Extended Data Fig. 8).

Extended Data Figure 6 Boulder size data.

Cumulative grain-size distribution for the Moses Coulee abandoned channel boulder bar (circles), Ephrata Fan basalt clasts (squares) and the Drumheller Channels boulder bar (triangles). Measurements were made of the intermediate grain diameter using a Wolman-style pebble count. The Ephrata Fan and Drumheller Channels sites are to the southwest of Moses Coulee and in a different flood pathway. The larger boulders at the Ephrata Fan and Drumheller Channels are assumed to originate as basalt columns that have been rounded by fluvial transport.

Extended Data Figure 7 Example model output showing the upper and lower shear stress thresholds for block sliding.

Round symbols depict the mean and bars depict one standard deviation (n = 33) of bed shear stress values extracted from one of the twelve 30,000-m2 polygons shown in Extended Data Fig. 7. In this example, the lower discharge bound (red symbol) for the threshold shear stress model is defined as the lowest discharge for which modelled shear stresses exceed the lower shear stress threshold for sliding. The high discharge bound (blue symbol) is defined as the lowest discharge with modelled shear stresses that exceed the upper shear stress threshold for sliding.

Extended Data Figure 8 Locations of the areas used to calculate mean bed shear stress.

The 30,000-m2 rectangles near the A–A′ cross-section were used to constrain discharges predicted by the threshold shear stress model. The larger 90,000-m2 polygons (labelled 1–6) were used to determine the shear stresses on the knickzone; the numbers correspond to the data in Extended Data Fig. 3.

Extended Data Figure 9 Schematic illustrating the method for defining the discharge range predicted by the threshold shear stress model.

For a given topographic reconstruction we first used the upper and lower bed stress thresholds for block plucking via sliding to define the range of possible discharges that are consistent with the threshold stress model at the lowest elevation site (Extended Data Fig. 7). The lowest elevation was always the canyon floor. We then followed the same procedure to determine the discharge range at sites with progressively higher elevations (for example, sites 2–5) that produced bed stress that were within the bounds for plucking at the site of interest and for all lower elevation sites. The range of discharges determined by these two criteria is shown by the green box. These two criteria are important because, for a flood discharge to be consistent with the threshold shear stress model, all sites that are inundated and eroding, from the canyon floor upward, must have bed stresses that are within the bounds for plucking. If the discharge required to pluck blocks at a higher elevation site exceed that of a lower elevation site, then the higher sites were considered to be dry and abandoned and so were not used to define the range of discharges for that stage of canyon incision.

Extended Data Figure 10 Predicted channel cross-sectional areas and widths.

a, b, Cross-sectional area (a) and channel width (b) predicted by the brim-full model and threshold shear stress model. The shading shows the range of predicted values based on upper- and lower-bound parameterizations of the critical dimensionless shear stress for bedrock incision by block sliding (see Methods). For the initial topography (bed elevation D), where basalt is primarily overlain by loess, modelled shear stresses are lower than the threshold for plucking. At bed elevation C, modelled shear stresses at brim-full discharge are within 5% of the lower threshold for plucking; hence, bed stresses are assumed to be sufficient for plucking when flow was brim-full. For all other bed topographies, brim-full discharge greatly exceeds predicted values for plucking and sediment initial motion. The letters A–D denote simulation results for bed elevations A–D; M denotes results for the modern topography.

PowerPoint slides

Source data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Larsen, I., Lamb, M. Progressive incision of the Channeled Scablands by outburst floods. Nature 538, 229–232 (2016). https://doi.org/10.1038/nature19817

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature19817

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing