Abstract
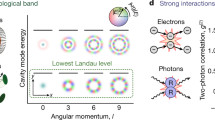
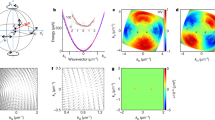
Synthetic photonic materials are an emerging platform for exploring the interface between microscopic quantum dynamics and macroscopic material properties1,2,3,4,5. Photons experiencing a Lorentz force develop handedness, providing opportunities to study quantum Hall physics and topological quantum science6,7,8. Here we present an experimental realization of a magnetic field for continuum photons. We trap optical photons in a multimode ring resonator to make a two-dimensional gas of massive bosons, and then employ a non-planar geometry to induce an image rotation on each round-trip9. This results in photonic Coriolis/Lorentz and centrifugal forces and so realizes the Fock–Darwin Hamiltonian for photons in a magnetic field and harmonic trap10. Using spatial- and energy-resolved spectroscopy, we track the resulting photonic eigenstates as radial trapping is reduced, finally observing a photonic Landau level at degeneracy. To circumvent the challenge of trap instability at the centrifugal limit10,11, we constrain the photons to move on a cone. Spectroscopic probes demonstrate flat space (zero curvature) away from the cone tip. At the cone tip, we observe that spatial curvature increases the local density of states, and we measure fractional state number excess consistent with the Wen–Zee theory, providing an experimental test of this theory of electrons in both a magnetic field and curved space12,13,14,15. This work opens the door to exploration of the interplay of geometry and topology, and in conjunction with Rydberg electromagnetically induced transparency, enables studies of photonic fractional quantum Hall fluids16,17 and direct detection of anyons18,19.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Peyronel, T. et al. Quantum nonlinear optics with single photons enabled by strongly interacting atoms. Nature 488, 57–60 (2012)
Gopalakrishnan, S., Lev, B. L. & Goldbart, P. M. Emergent crystallinity and frustration with Bose–Einstein condensates in multimode cavities. Nat. Phys. 5, 845–850 (2009)
Baumann, K., Guerlin, C., Brennecke, F. & Esslinger, T. Dicke quantum phase transition with a superfluid gas in an optical cavity. Nature 464, 1301–1306 (2010)
Cooper, N. R. & Dalibard, J. Reaching fractional quantum Hall states with optical flux lattices. Phys. Rev. Lett. 110, 185301 (2013)
Carusotto, I. & Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 85, 299–366 (2013)
Jia, N., Owens, C., Sommer, A., Schuster, D. & Simon, J. Time- and site-resolved dynamics in a topological circuit. Phys. Rev. X 5, 021031 (2015)
Otterbach, J., Ruseckas, J., Unanyan, R. G., Juzeliūnas, G. & Fleischhauer, M. Effective magnetic fields for stationary light. Phys. Rev. Lett. 104, 033903 (2010)
Wang, Z., Chong, Y., Joannopoulos, J. D. & Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009)
Yuan, J. et al. Nonplanar ring resonator modes: generalized Gaussian beams. Appl. Opt. 46, 2980–2989 (2007)
Cooper, N. R. Rapidly rotating atomic gases. Adv. Phys. 57, 539–616 (2008)
Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964 (2008)
Wen, X. G. & Zee, A. Shift and spin vector: new topological quantum numbers for the Hall fluids. Phys. Rev. Lett. 69, 953–956 (1992)
Hoyos, C. & Son, D. T. Hall viscosity and electromagnetic response. Phys. Rev. Lett. 108, 066805 (2012)
Abanov, A. G. & Gromov, A. Electromagnetic and gravitational responses of two-dimensional noninteracting electrons in a background magnetic field. Phys. Rev. B 90, 014435 (2014)
Can, T., Laskin, M. & Wiegmann, P. Fractional quantum Hall effect in a curved space: gravitational anomaly and electromagnetic response. Phys. Rev. Lett. 113, 046803 (2014)
Sommer, A., Büchler, H. P. & Simon, J. Quantum crystals and Laughlin droplets of cavity Rydberg polaritons. Preprint at http://arXiv.org/abs/1506.00341 (2015)
Umucalılar, R. O., Wouters, M. & Carusotto, I. Probing few-particle Laughlin states of photons via correlation measurements. Phys. Rev. A 89, 023803 (2014)
Paredes, B., Fedichev, P., Cirac, J. I. & Zoller, P. 1/2-Anyons in small atomic Bose-Einstein condensates. Phys. Rev. Lett. 87, 010402 (2001)
Umucalılar, R. O. & Carusotto, I. Many-body braiding phases in a rotating strongly correlated photon gas. Phys. Lett. A 377, 2074–2078 (2013)
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. Non-Abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008)
Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 100, (2008)
Rechtsman, M. C. et al. Photonic Floquet topological insulators. Nature 496, 196–200 (2013)
Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013)
Rechtsman, M. C. et al. Strain-induced pseudomagnetic field and photonic Landau levels in dielectric structures. Nat. Photon. 7, 153–158 (2013)
Karzig, T., Bardyn, C.-E., Lindner, N. H. & Refael, G. Topological polaritons. Phys. Rev. X 5, 031001 (2015)
Longhi, S. Synthetic gauge fields for light beams in optical resonators. Opt. Lett. 40, 2941–2944 (2015)
Klaers, J., Schmitt, J., Vewinger, F. & Weitz, M. Bose-Einstein condensation of photons in an optical microcavity. Nature 468, 545–548 (2010)
Sommer, A. & Simon, J. Engineering photonic Floquet Hamiltonians through Fabry–Pérot resonators. New J. Phys. 18, 035008 (2016)
Schweikhard, V., Coddington, I., Engels, P., Mogendorff, V. P. & Cornell, E. A. Rapidly rotating Bose-Einstein condensates in and near the lowest Landau level. Phys. Rev. Lett. 92, 040404 (2004)
Read, N. Non-Abelian adiabatic statistics and Hall viscosity in quantum Hall states and p x + ip y paired superfluids. Phys. Rev. B 79, 045308 (2009)
Acknowledgements
We acknowledge conversations with I. Carusotto, M. Levin and P. Wiegmann. This work was supported by DOE, DARPA and AFOSR. A.G. acknowledges the support of the Kadanoff Center for Theoretical Physics. A.R. acknowledges support from ARO through an NDSEG fellowship.
Author information
Authors and Affiliations
Contributions
The experiment was designed and built by N.S., J.S., A.R. and A.S. Measurement and analysis of the data was performed by N.S. Theoretical development and interpretation of results were performed by J.S., A.S., N.S. and A.G. All authors contributed to the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-3 and additional references. (PDF 1769 kb)
Rights and permissions
About this article
Cite this article
Schine, N., Ryou, A., Gromov, A. et al. Synthetic Landau levels for photons. Nature 534, 671–675 (2016). https://doi.org/10.1038/nature17943
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature17943
This article is cited by
-
Topological phenomena at defects in acoustic, photonic and solid-state lattices
Nature Reviews Physics (2023)
-
Resource Theory of Heat and Work with Non-commuting Charges
Annales Henri Poincaré (2023)
-
Electronic materials with nanoscale curved geometries
Nature Electronics (2022)
-
Chiral cavity quantum electrodynamics
Nature Physics (2022)
-
Atom-optically synthetic gauge fields for a noninteracting Bose gas
Light: Science & Applications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.