Abstract
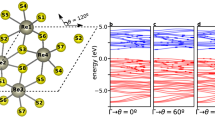
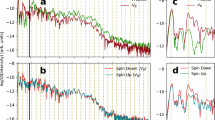
Strong-field laser excitation of solids can produce extremely nonlinear electronic and optical behaviour. As recently demonstrated, this includes the generation of high harmonics extending into the vacuum-ultraviolet and extreme-ultraviolet regions of the electromagnetic spectrum1,2,3,4,5,6,7,8. High harmonic generation is shown to occur fundamentally differently in solids and in dilute atomic gases1,2,3,4,5,6,9,10,11,12,13. How the microscopic mechanisms in the solid and the gas differ remains a topic of intense debate1,2,3,4,5,6,7,8,9,10,11,14,15,16,17,18. Here we report a direct comparison of high harmonic generation in the solid and gas phases of argon and krypton. Owing to the weak van der Waals interaction, rare (noble)-gas solids are a near-ideal medium in which to study the role of high density and periodicity in the generation process. We find that the high harmonic generation spectra from the rare-gas solids exhibit multiple plateaus extending well beyond the atomic limit of the corresponding gas-phase harmonics measured under similar conditions. The appearance of multiple plateaus indicates strong interband couplings involving multiple single-particle bands. We also compare the dependence of the solid and gas harmonic yield on laser ellipticity and find that they are similar, suggesting the importance of electron–hole recollision in these solids. This implies that gas-phase methods such as polarization gating for attosecond pulse generation and orbital tomography could be realized in solids.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. Nature Phys. 7, 138–141 (2011)
Ghimire, S. et al. Strong-field and attosecond physics in solids. J. Phys. At. Mol. Opt. Phys. 47, 204030 (2014)
Ghimire, S. et al. Redshift in the optical absorption of ZnO single crystals in the presence of an intense midinfrared laser field. Phys. Rev. Lett. 107, 167407 (2011)
Luu, T. T. et al. Extreme ultraviolet high-harmonic spectroscopy of solids. Nature 521, 498–502 (2015)
Schubert, O. et al. Sub-cycle control of terahertz high-harmonic generation by dynamical Bloch oscillations. Nature Photon. 8, 119–123 (2014)
Hohenleutner, M. et al. Real-time observation of interfering crystal electrons in high-harmonic generation. Nature 523, 572–575 (2015)
Vampa, G. et al. Linking high harmonics from gases and solids. Nature 522, 462–464 (2015)
Vampa, G. et al. All-optical reconstruction of crystal band structure. Phys. Rev. Lett. 115, 193603 (2015)
Ghimire, S. et al. Generation and propagation of high-order harmonics in crystals. Phys. Rev. A 85, 043836 (2012)
Wu, M., Ghimire, S., Reis, D. A., Schafer, K. J. & Gaarde, M. B. High-harmonic generation from Bloch electrons in solids. Phys. Rev. A 91, 043839 (2015)
Korbman, M., Yu Kruchinin, S. & Yakovlev, V. S. Quantum beats in the polarization response of a dielectric to intense few-cycle laser pulses. New J. Phys. 15, 013006 (2013)
Corkum, P. B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 71, 1994–1997 (1993)
Krause, J. L., Schafer, K. J. & Kulander, K. C. High-order harmonic generation from atoms and ions in the high intensity regime. Phys. Rev. Lett. 68, 3535–3538 (1992)
Vampa, G. et al. Theoretical analysis of high-harmonic generation in solids. Phys. Rev. Lett. 113, 073901 (2014)
McDonald, C. R., Vampa, G., Corkum, P. B. & Brabec, T. Interband Bloch oscillation mechanism for high-harmonic generation in semiconductor crystals. Phys. Rev. A 92, 033845 (2015)
Vampa, G., McDonald, C. R., Orlando, G., Corkum, P. B. & Brabec, T. Semiclassical analysis of high harmonic generation in bulk crystals. Phys. Rev. B 91, 064302 (2015)
Higuchi, T., Stockman, M. I. & Hommelhoff, P. Strong-Field Perspective on High-Harmonic Radiation from Bulk Solids. Phys. Rev. Lett. 113, 213901 (2014)
Golde, D., Meier, T. & Koch, S. W. Microscopic analysis of high-harmonic generation in semiconductor nanostructures. Phys. Status Solidi C 6, 420–423 (2009)
Budil, K. S., Salières, P., L’Huillier, A., Ditmire, T. & Perry, M. D. Influence of ellipticity on harmonic generation. Phys. Rev. A 48, R3437–R3440 (1993)
Burnett, N. H., Kan, C. & Corkum, P. B. Ellipticity and polarization effects in harmonic generation in ionizing neon. Phys. Rev. A 51, R3418–R3421 (1995)
Klein, M. L. & Venables, J. A. Rare Gas Solids 123 (Academic Press, 1976)
Bacalis, N. C., Papaconstantopoulos, D. A. & Pickett, W. E. Systematic calculations of the band structures of the rare-gas crystals neon, argon, krypton, and xenon. Phys. Rev. B 38, 6218–6226 (1988)
Gauthey, F. I., Garraway, B. M. & Knight, P. L. High harmonic generation and periodic level crossings. Phys. Rev. A 56, 3093–3096 (1997)
Blaha, P., Schwarz, K., Madsen, G., Kvasnicka, D. & Luitz, J. WIEN2k, An Augmented Plane Wave Plus + Local Orbitals Program for Calculating Crystal Properties (TU Wien, 2001)
Shan, B., Ghimire, S. & Chang, Z. Generation of the attosecond extreme ultraviolet supercontinuum by a polarization gating. J. Mod. Opt. 52, 277–283 (2005)
Itatani, J. et al. Tomographic imaging of molecular orbitals. Nature 432, 867–871 (2004)
Ndabashimiye, G., Ghimire, S., Reis, D. & Nicholson, D. Measurement of coherence lengths of below threshold harmonics in solid argon. Opt. Soc. Am. Tech. Dig. QW1A.7 http://dx.doi.org/10.1364/CLEO_QELS.2013.QW1A.7 (2013)
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996)
Tran, F. & Blaha, P. Accurate band gaps of semiconductors and insulators with a semilocal exchange-correlation potential. Phys. Rev. Lett. 102, 226401 (2009)
Acknowledgements
At Stanford/SLAC, this work was supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences, through the AMOS programme within the Chemical Sciences Division (G.N., D.A.R.) and the Office of Science Early Career Research Program (S.G.). At Louisiana State University this work is supported by the National Science Foundation under grant number PHY-1403236. Solid Ar samples were characterized at Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, the use of which is supported by the US Department of Energy, Office of Science, Office of Basic Energy Sciences under contract number DE AC02-76SF00515.
Author information
Authors and Affiliations
Contributions
G.N., S.G. and D.A.R. conceived the experiments. G.N. performed the experiment and analysed the data. M.W., K.J.S., and M.B.G. developed the single electron laser excitation theory and performed the calculation. D.A.B. performed the DFT calculations. All authors contributed to the interpretation of the results and writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Ndabashimiye, G., Ghimire, S., Wu, M. et al. Solid-state harmonics beyond the atomic limit. Nature 534, 520–523 (2016). https://doi.org/10.1038/nature17660
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature17660
This article is cited by
-
Observation of interband Berry phase in laser-driven crystals
Nature (2024)
-
Lightwave electronics in condensed matter
Nature Reviews Materials (2023)
-
Emerging ultrafast techniques for studying quantum materials
Nature Reviews Materials (2023)
-
Orbital perspective on high-harmonic generation from solids
Nature Communications (2023)
-
High-order harmonic generation in laser-induced low-density plasma: past and recent achievements
Applied Physics B (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.