Abstract
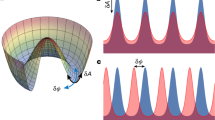
Ferrofluids exhibit unusual hydrodynamic effects owing to the magnetic nature of their constituents. As magnetization increases, a classical ferrofluid undergoes a Rosensweig instability1 and creates self-organized, ordered surface structures2 or droplet crystals3. Quantum ferrofluids such as Bose–Einstein condensates with strong dipolar interactions also display superfluidity4. The field of dipolar quantum gases is motivated by the search for new phases of matter that break continuous symmetries5,6. The simultaneous breaking of continuous symmetries such as the phase invariance in a superfluid state and the translational symmetry in a crystal provides the basis for these new states of matter. However, interaction-induced crystallization in a superfluid has not yet been observed. Here we use in situ imaging to directly observe the spontaneous transition from an unstructured superfluid to an ordered arrangement of droplets in an atomic dysprosium Bose–Einstein condensate7. By using a Feshbach resonance to control the interparticle interactions, we induce a finite-wavelength instability8 and observe discrete droplets in a triangular structure, the number of which grows as the number of atoms increases. We find that these structured states are surprisingly long-lived and observe hysteretic behaviour, which is typical for a crystallization process and in close analogy to the Rosensweig instability. Our system exhibits both superfluidity and, as we show here, spontaneous translational symmetry breaking. Although our observations do not probe superfluidity in the structured states, if the droplets establish a common phase via weak links, then our system is a very good candidate for a supersolid ground state9,10,11.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Rosensweig, R. Ferrohydrodynamics Ch. 7.1 (Cambridge Univ. Press, 1985)
Cowley, M. D. & Rosensweig, R. E. The interfacial stability of a ferromagnetic fluid. J. Fluid Mech. 30, 671–688 (1967)
Timonen, J. V. I., Latikka, M., Leibler, L., Ras, R. H. A. & Ikkala, O. Switchable static and dynamic self-assembly of magnetic droplets on superhydrophobic surfaces. Science 341, 253–257 (2013)
Lahaye, T. et al. Strong dipolar effects in a quantum ferrofluid. Nature 448, 672–675 (2007)
Lahaye, T., Menotti, C., Santos, L., Lewenstein, M. & Pfau, T. The physics of dipolar bosonic quantum gases. Rep. Prog. Phys. 72, 126401 (2009)
Baranov, M. A., Dalmonte, M., Pupillo, G. & Zoller, P. Condensed matter theory of dipolar quantum gases. Chem. Rev. 112, 5012–5061 (2012)
Lu, M., Burdick, N. Q., Youn, S. H. & Lev, B. L. Strongly dipolar Bose-Einstein condensate of dysprosium. Phys. Rev. Lett. 107, 190401 (2011)
Santos, L., Shlyapnikov, G. V. & Lewenstein, M. Roton-Maxon spectrum and stability of trapped dipolar Bose-Einstein condensates. Phys. Rev. Lett. 90, 250403 (2003)
Andreev, A. F. & Lifshitz, I. M. Quantum theory of defects in crystals. Sov. Phys. JETP 29, 1107–1113 (1969)
Chester, G. V. Speculations on Bose-Einstein condensation and quantum crystals. Phys. Rev. A 2, 256–258 (1970)
Leggett, A. J. Can a solid be “superfluid”? Phys. Rev. Lett. 25, 1543–1546 (1970)
Kim, E. & Chan, M. H. W. Probable observation of a supersolid helium phase. Nature 427, 225–227 (2004)
Kim, E. & Chan, M. H. W. Observation of superflow in solid helium. Science 305, 1941–1944 (2004)
Kim, D. Y. & Chan, M. H. W. Absence of supersolidity in solid helium in porous Vycor glass. Phys. Rev. Lett. 109, 155301 (2012)
Henshaw, D. G. & Woods, A. D. B. Modes of atomic motions in liquid helium by inelastic scattering of neutrons. Phys. Rev. 121, 1266–1274 (1961)
Ronen, S., Bortolotti, D. C. E. & Bohn, J. L. Radial and angular rotons in trapped dipolar gases. Phys. Rev. Lett. 98, 030406 (2007)
Saito, H., Kawaguchi, Y. & Ueda, M. Ferrofluidity in a two-component dipolar Bose-Einstein condensate. Phys. Rev. Lett. 102, 230403 (2009)
Wilson, R. M., Ronen, S. & Bohn, J. L. Angular collapse of dipolar Bose-Einstein condensates. Phys. Rev. A 80, 023614 (2009)
Maier, T., Kadau, H., Schmitt, M., Griesmaier, A. & Pfau, T. Narrow-line magneto-optical trap for dysprosium atoms. Opt. Lett. 39, 3138–3141 (2014)
Maier, T. et al. Emergence of chaotic scattering in ultracold Er and Dy. Phys. Rev. X 5, 041029 (2015)
Góral, K., Rząż ewski, K. & Pfau, T. Bose-Einstein condensation with magnetic dipole-dipole forces. Phys. Rev. A 61, 051601 (2000)
Stuhler, J. et al. Observation of dipole-dipole interaction in a degenerate quantum gas. Phys. Rev. Lett. 95, 150406 (2005)
Koch, T. et al. Stabilization of a purely dipolar quantum gas against collapse. Nature Phys . 4, 218–222 (2008)
Tang, Y., Sykes, A., Burdick, N. Q., Bohn, J. L. & Lev, B. L. s-wave scattering lengths of the strongly dipolar bosons 162Dy and 164Dy. Phys. Rev. A 92, 022703 (2015)
Maier, T. et al. Broad universal Feshbach resonances in the chaotic spectrum of dysprosium atoms. Phys. Rev. A 92, 060702(R) (2015)
Bradley, C. C., Sackett, C. A. & Hulet, R. G. Bose-Einstein condensation of lithium: observation of limited condensate number. Phys. Rev. Lett. 78, 985–989 (1997)
Lee, T. D., Huang, K. & Yang, C. N. Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties. Phys. Rev. 106, 1135–1145 (1957)
Petrov, D. S. Quantum mechanical stabilization of a collapsing Bose-Bose mixture. Phys. Rev. Lett. 115, 155302 (2015)
Lima, A. R. P. & Pelster, A. Quantum fluctuations in dipolar Bose gases. Phys. Rev. A 84, 041604 (2011)
Saccani, S., Moroni, S. & Boninsegni, M. Excitation spectrum of a supersolid. Phys. Rev. Lett. 108, 175301 (2012)
Acknowledgements
We thank A. Griesmaier for support at the early stage of the experiment and D. Zajec, D. Peter, H. P. Büchler and L. Santos for discussions. This work is supported by the German Research Foundation (DFG) within SFB/TRR21. H.K. acknowledges support by the ‘Studienstiftung des deutschen Volkes’.
Author information
Authors and Affiliations
Contributions
All authors discussed the results, made critical contributions to the work and contributed to the writing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Atom trap-loss spectroscopy for two Feshbach resonances.
Atom-loss spectroscopy mapping Feshbach resonances of 164Dy. The number of atoms (blue circles) and temperature (red diamonds) are normalized. a, The atom-number minimum shows the centre of the Feshbach resonance at B0 = 1.326(3) G, while the temperature is maximized at B0 + ΔB, with ΔB = 8(5) mG. We prepared stable BECs at B = 1.285(3) G (dashed black line) before we induced an instability for lower magnetic-field values. b, For the data presented in the main text, we used a resonance at B0 = 7.117(3) G (the atom-number minimum) with ΔB = 51(15) mG. Stable BECs were created at B = 6.962(3) G (dashed black line).
Rights and permissions
About this article
Cite this article
Kadau, H., Schmitt, M., Wenzel, M. et al. Observing the Rosensweig instability of a quantum ferrofluid. Nature 530, 194–197 (2016). https://doi.org/10.1038/nature16485
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature16485
This article is cited by
-
Collective Excitations of Bose–Einstein Condensate in a Rydberg Atom
Journal of Low Temperature Physics (2024)
-
Exploring the vibrational series of pure trilobite Rydberg molecules
Nature Communications (2023)
-
Heating a dipolar quantum fluid into a solid
Nature Communications (2023)
-
Supersolidity in ultracold dipolar gases
Nature Reviews Physics (2023)
-
Collisionally stable gas of bosonic dipolar ground-state molecules
Nature Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.