Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Observation of non-Hermitian degeneracies in a chaotic exciton-polariton billiard

Nature volume 526, pages 554–558 (2015)Cite this article

Subjects

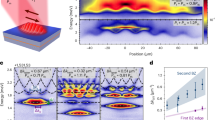
Abstract

Exciton-polaritons are hybrid light–matter quasiparticles formed by strongly interacting photons and excitons (electron–hole pairs) in semiconductor microcavities1,2,3. They have emerged as a robust solid-state platform for next-generation optoelectronic applications as well as for fundamental studies of quantum many-body physics. Importantly, exciton-polaritons are a profoundly open (that is, non-Hermitian4,5) quantum system, which requires constant pumping of energy and continuously decays, releasing coherent radiation6. Thus, the exciton-polaritons always exist in a balanced potential landscape of gain and loss. However, the inherent non-Hermitian nature of this potential has so far been largely ignored in exciton-polariton physics. Here we demonstrate that non-Hermiticity dramatically modifies the structure of modes and spectral degeneracies in exciton-polariton systems, and, therefore, will affect their quantum transport, localization and dynamical properties7,8,9. Using a spatially structured optical pump10,11,12, we create a chaotic exciton-polariton billiard—a two-dimensional area enclosed by a curved potential barrier. Eigenmodes of this billiard exhibit multiple non-Hermitian spectral degeneracies, known as exceptional points13,14. Such points can cause remarkable wave phenomena, such as unidirectional transport15, anomalous lasing/absorption16,17 and chiral modes18. By varying parameters of the billiard, we observe crossing and anti-crossing of energy levels and reveal the non-trivial topological modal structure exclusive to non-Hermitian systems9,13,14,15,16,17,18,19,20,21,22. We also observe mode switching and a topological Berry phase for a parameter loop encircling the exceptional point23,24. Our findings pave the way to studies of non-Hermitian quantum dynamics of exciton-polaritons, which may uncover novel operating principles for polariton-based devices.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Non-Hermitian exciton-polariton Sinai billiard and its spectrum.
Figure 2: Crossing and anti-crossing for two near-degenerate modes.
Figure 3: Eigenvalues of a two-level non-Hermitian model in the vicinity of the exceptional point.
Figure 4: Observation of the topological Berry phase acquired after circling around the exceptional point in the parameter plane.

Similar content being viewed by others

References

  1. Kasprzak, J. et al. Bose–Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006)

    Article  ADS  CAS  Google Scholar 

  2. Deng, H., Haug, H. & Yamamoto, Y. Exciton-polariton Bose–Einstein condensation. Rev. Mod. Phys. 82, 1489–1537 (2010)

    Article  ADS  CAS  Google Scholar 

  3. Carusotto, I. & Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 85, 299–366 (2013)

    Article  ADS  Google Scholar 

  4. Moiseyev, N. Non-Hermitian Quantum Mechanics (Cambridge Univ. Press, 2011)

    Book  Google Scholar 

  5. Bender, C. M. Making sense of non-Hermitian Hamiltonians. Rep. Prog. Phys. 70, 947–1018 (2007)

    Article  ADS  MathSciNet  Google Scholar 

  6. Savvidis, P. G. et al. Off-branch polaritons and multiple scattering in semiconductor microcavities. Phys. Rev. B 64, 075311 (2001)

    Article  ADS  Google Scholar 

  7. Berry, M. V. Quantizing a classically ergodic system: Sinai’s billiard and the KKR method. Ann. Phys. 131, 163–216 (1981)

    Article  ADS  MathSciNet  Google Scholar 

  8. Guhr, T., Müller-Groeling, A. & Weidenmüller, H. A. Random-matrix theories in quantum physics: common concepts. Phys. Rep. 299, 189–425 (1998)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  9. Bliokh, K. Y., Bliokh, Y. P., Freilikher, V., Genack, A. Z. & Sebbah, P. Coupling and level repulsion in the localized regime: from isolated to quasiextended modes. Phys. Rev. Lett. 101, 133901 (2008)

    Article  ADS  CAS  Google Scholar 

  10. Tosi, G. et al. Sculpting oscillators with light within a nonlinear quantum fluid. Nature Phys. 8, 190–194 (2012)

    Article  ADS  CAS  Google Scholar 

  11. Sanvitto, D. et al. All-optical control of the quantum flow of a polariton condensate. Nature Photon. 5, 610–614 (2011)

    Article  ADS  CAS  Google Scholar 

  12. Dall, R. et al. Creation of orbital angular momentum states with chiral polaritonic lenses. Phys. Rev. Lett. 113, 200404 (2014)

    Article  ADS  Google Scholar 

  13. Berry, M. V. Physics of non-Hermitian degeneracies. Czech. J. Phys. 54, 1039–1047 (2004)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  14. Heiss, W. D. The physics of exceptional points. J. Phys. Math. Gen. 45, 444016 (2012)

    Article  ADS  MathSciNet  Google Scholar 

  15. Guo, A. et al. Observation of PT-symmetry breaking in complex optical potentials. Phys. Rev. Lett. 103, 093902 (2009)

    Article  ADS  CAS  Google Scholar 

  16. Peng, B. et al. Loss-induced suppression and revival of lasing. Science 346, 328–332 (2014)

    Article  ADS  CAS  Google Scholar 

  17. Sun, Y., Tan, W., Li, H.-Q., Li, J. & Chen, H. Experimental demonstration of a coherent perfect absorber with PT phase transition. Phys. Rev. Lett. 112, 143903 (2014)

    Article  ADS  Google Scholar 

  18. Dembowski, C. et al. Observation of a chiral state in a microwave cavity. Phys. Rev. Lett. 90, 034101 (2003)

    Article  ADS  CAS  Google Scholar 

  19. Cao, H. & Wiersig, J. Dielectric microcavities: model systems for wave chaos and non-Hermitian physics. Rev. Mod. Phys. 87, 61–111 (2015)

    Article  ADS  MathSciNet  Google Scholar 

  20. Dembowski, C. et al. Experimental observation of the topological structure of exceptional points. Phys. Rev. Lett. 86, 787–790 (2001)

    Article  ADS  CAS  Google Scholar 

  21. Lee, S.-B. et al. Observation of an exceptional point in a chaotic optical microcavity. Phys. Rev. Lett. 103, 134101 (2009)

    Article  ADS  Google Scholar 

  22. Choi, Y. et al. Quasi-eigenstate coalescence in an atomic-cavity quantum composite. Phys. Rev. Lett. 104, 153601 (2010)

    Article  ADS  Google Scholar 

  23. Heiss, W. D. Phases of wave functions and level repulsion. Eur. Phys. J. D 7, 1–4 (1999)

    Article  ADS  CAS  Google Scholar 

  24. Dembowski, C. et al. Encircling an exceptional point. Phys. Rev. E 69, 056216 (2004)

    Article  ADS  CAS  Google Scholar 

  25. Akis, R., Ferry, D. K. & Bird, J. P. Wave function scarring effects in open stadium shaped quantum dots. Phys. Rev. Lett. 79, 123–126 (1997)

    Article  ADS  CAS  Google Scholar 

  26. Milner, V., Hanssen, J. L., Campbell, W. C. & Raizen, M. G. Optical billiards for atoms. Phys. Rev. Lett. 86, 1514–1517 (2001)

    Article  ADS  CAS  Google Scholar 

  27. Kaplan, A., Friedman, N., Anderson, M. & Davidson, N. Observation of islands of stability in soft wall atom-optics billiards. Phys. Rev. Lett. 87, 274101 (2001)

    Article  ADS  CAS  Google Scholar 

  28. Ponomarenko, L. A. et al. Chaotic Dirac billiard in graphene quantum dots. Science 320, 356–358 (2008)

    Article  ADS  CAS  Google Scholar 

  29. Uzdin, R., Mailybaev, A. & Moiseyev, N. On the observability and asymmetry of adiabatic state flips generated by exceptional points. J. Phys. A 44, 435302 (2011)

    Article  ADS  MathSciNet  Google Scholar 

  30. Berry, M. V. & Uzdin, R. Slow non-Hermitian cycling: exact solutions and the Stokes phenomenon. J. Phys. A 44, 435303 (2011)

    Article  ADS  MathSciNet  Google Scholar 

  31. Kavokin, A., Baumberg, J., Malpuech, G. & Laussy, F. Microcavities (Oxford Univ. Press, 2007)

    Book  Google Scholar 

  32. Sinai, Y. G. Dynamical systems with elastic reflections. Russ. Math. Surv. 25, 137–189 (1970)

    Article  Google Scholar 

  33. Keeling, J. & Berloff, N. G. Spontaneous rotating vortex lattices in a pumped decaying condensate. Phys. Rev. Lett. 100, 250401 (2008)

    Article  ADS  Google Scholar 

  34. Cristofolini, P. et al. Optical superfluid phase transitions and trapping of polariton condensates. Phys. Rev. Lett. 110, 186403 (2013)

    Article  ADS  CAS  Google Scholar 

  35. Askitopoulos, A. et al. A robust platform for engineering pure-quantum-state transitions in polariton condensates. Phys. Rev. B 92, 035305 (2015)

    Article  ADS  Google Scholar 

  36. Wouters, M. & Carusotto, I. Excitations in a nonequilibrium Bose–Einstein condensate of exciton polaritons. Phys. Rev. Lett. 99, 140402 (2007)

    Article  ADS  Google Scholar 

  37. Smirnov, L. A., Smirnova, D. A., Ostrovskaya, E. A. & Kivshar, Yu. S. Dynamics and stability of dark solitons in exciton-polariton condensates. Phys. Rev. B 89, 235310 (2014)

    Article  ADS  Google Scholar 

  38. Wouters, M. Energy relaxation in the mean-field description of polariton condensates. New J. Phys. 14, 075020 (2012)

    Article  ADS  Google Scholar 

  39. Wertz, E. et al. Propagation and amplification dynamics of 1D polariton condensates. Phys. Rev. Lett. 109, 216404 (2012)

    Article  ADS  CAS  Google Scholar 

  40. Eastham, P. R. Mode locking and mode competition in a nonequilibrium solid-state condensate. Phys. Rev. B 78, 035319 (2008)

    Article  ADS  Google Scholar 

  41. Ge, L. & Stone, A. D. Parity-time symmetry breaking beyond one dimension: the role of degeneracy. Phys. Rev. X 4, 031011 (2014)

    Google Scholar 

Download references

Acknowledgements

We thank M. Berry and O. Kirillov for comments. This research was supported by the Australian Research Council, the ImPACT Program of the Council for Science, Technology and Innovation (Cabinet Office, Government of Japan), the RIKEN iTHES Project, the MURI Center for Dynamic Magneto-Optics, a Grant-in-Aid for Scientific Research (type A), and the State of Bavaria.

Author information

Authors and Affiliations

  1. Research School of Physics and Engineering, The Australian National University, Canberra, 2601, Australian Capital Territory, Australia

    T. Gao, E. Estrecho, K. Y. Bliokh, Y. S. Kivshar, A. G. Truscott, R. G. Dall & E. A. Ostrovskaya

  2. Center for Emergent Matter Science, RIKEN, Wako-shi, 351-0198, Saitama, Japan

    K. Y. Bliokh, M. D. Fraser & F. Nori

  3. School of Physical and Mathematical Sciences, Nanyang Technological University, Singapore, 637371, Singapore

    T. C. H. Liew

  4. Technische Physik and Wilhelm-Conrad-Röntgen Research Center for Complex Material Systems, Universität Würzburg, Am Hubland, D-97074, Würzburg, Germany

    S. Brodbeck, M. Kamp, C. Schneider & S. Höfling

  5. SUPA, School of Physics and Astronomy, University of St Andrews, St Andrews, KY16 9SS, UK

    S. Höfling

  6. ImPACT Project, Japan Science and Technology Agency, Chiyoda-ku, 102-0076, Tokyo, Japan

    Y. Yamamoto

  7. Edward L. Ginzton Laboratory, Stanford University, Stanford, 94305-4085, California, USA

    Y. Yamamoto

  8. Physics Department, University of Michigan, Ann Arbor, 48109-1040, Michigan, USA

    F. Nori

Authors
  1. T. Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. E. Estrecho
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. Y. Bliokh
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. T. C. H. Liew
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. M. D. Fraser
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. S. Brodbeck
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. M. Kamp
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. C. Schneider
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. S. Höfling
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. Y. Yamamoto
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. F. Nori
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. Y. S. Kivshar
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. A. G. Truscott
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. R. G. Dall
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. E. A. Ostrovskaya
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

E.A.O., T.G., E.E. and K.Y.B. conceived the idea for this research; T.G., E.E., M.D.F., R.G.D. and A.G.T. designed and built the experiment with conceptual contributions from E.A.O.; T.G., E.E. and R.G.D. collected and analysed experimental data; K.Y.B, E.E., T.C.H.L. and E.A.O. performed theoretical and numerical analysis; S.B., M.K., C.S. and S.H. fabricated and characterized the semiconductor microcavity; E.A.O. and K.Y.B. wrote the paper with input from T.G., E.E. and T.C.H.L.; F.N., M.D.F., A.G.T, S.H., Y.Y. and Y.S.K. contributed to discussions and the shaping of the manuscript.

Corresponding author

Correspondence to E. A. Ostrovskaya.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Extended data figures and tables

Extended Data Figure 1 Diagram of the experimental apparatus.

See Methods for details.

Extended Data Figure 2 Schematics of the optically induced billiard potential with two different wall thicknesses.

a, Thin walls; b, thick walls. The active regions corresponding to the optical pump are shown in black, and we note that the enclosed area does not change with wall thickness.

Extended Data Figure 3 Effect of wall thickness on spectroscopic line profiles of the Sinai billiard.

a, b, Profiles are shown in the vicinity of the degeneracy for the levels highlighted in Fig. 1c, d with thick (a) and thin (b) walls. The thick lines demonstrate the principle of data extraction for anti-crossing (a) and crossing (b) of the energy levels corresponding to those shown in Fig. 2a and b, respectively

Extended Data Figure 4 Spatial density distribution of the first seven simultaneously populated lowest-energy modes of the Sinai billiard.

Spatial density distributions were obtained from the thick-wall setup (Extended Data Fig. 2b) with R/W = 0.35. Top row, experimentally imaged; middle row, calculated using the effective linear potential model; bottom row, calculated using the full dynamical model given by equation (2).

Extended Data Figure 5 Spatial modes in the hybridization regions.

a–g, Calculated spatial modes; each panel shows the modulus squared of the wavefunction (left) and the wavefunction’s phase distribution (right, colour coded). a, b, e, f, Numerically calculated pure spatial eigenstates (modes 3 (a, e) and 4 (b, f)) for the Sinai billiard with thick and thin walls in the corresponding hybridization regions shown in Fig. 2a and b, respectively. c, d, g, The superpositions of modes 3 and 4 that match the experimentally imaged modes shown in Fig. 2; c (boxed in blue) and d (boxed in red) correspond to the blue and red curves of Fig. 2a, respectively, while g (boxed in red and blue) corresponds to the crossing point in Fig. 2b. The relative populations of pure modes in the superposition states are: c, |α|2 = 0.85 and |β|2 = 0.15; d, |α|2 = 0.65 and |β|2 = 0.35; g, |α|2 = 0.60 and |β|2 = 0.40.

PowerPoint slides

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Gao, T., Estrecho, E., Bliokh, K. et al. Observation of non-Hermitian degeneracies in a chaotic exciton-polariton billiard. Nature 526, 554–558 (2015). https://doi.org/10.1038/nature15522

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature15522

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing