Spawning rings of exceptional points out of Dirac cones

Abstract

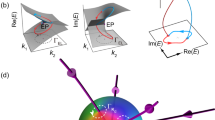
The Dirac cone underlies many unique electronic properties of graphene¹ and topological insulators, and its band structure—two conical bands touching at a single point—has also been realized for photons in waveguide arrays², atoms in optical lattices³, and through accidental degeneracy^4,5. Deformation of the Dirac cone often reveals intriguing properties; an example is the quantum Hall effect, where a constant magnetic field breaks the Dirac cone into isolated Landau levels. A seemingly unrelated phenomenon is the exceptional point^6,7, also known as the parity–time symmetry breaking point^8,9,10,11, where two resonances coincide in both their positions and widths. Exceptional points lead to counter-intuitive phenomena such as loss-induced transparency¹², unidirectional transmission or reflection^11,13,14, and lasers with reversed pump dependence¹⁵ or single-mode operation^16,17. Dirac cones and exceptional points are connected: it was theoretically suggested that certain non-Hermitian perturbations can deform a Dirac cone and spawn a ring of exceptional points^18,19,20. Here we experimentally demonstrate such an ‘exceptional ring’ in a photonic crystal slab. Angle-resolved reflection measurements of the photonic crystal slab reveal that the peaks of reflectivity follow the conical band structure of a Dirac cone resulting from accidental degeneracy, whereas the complex eigenvalues of the system are deformed into a two-dimensional flat band enclosed by an exceptional ring. This deformation arises from the dissimilar radiation rates of dipole and quadrupole resonances, which play a role analogous to the loss and gain in parity–time symmetric systems. Our results indicate that the radiation existing in any open system can fundamentally alter its physical properties in ways previously expected only in the presence of material loss and gain.