Abstract
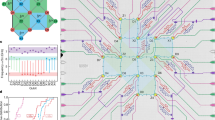
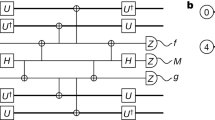
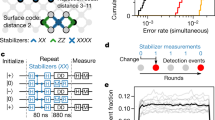
Quantum computing becomes viable when a quantum state can be protected from environment-induced error. If quantum bits (qubits) are sufficiently reliable, errors are sparse and quantum error correction (QEC)1,2,3,4,5,6 is capable of identifying and correcting them. Adding more qubits improves the preservation of states by guaranteeing that increasingly larger clusters of errors will not cause logical failure—a key requirement for large-scale systems. Using QEC to extend the qubit lifetime remains one of the outstanding experimental challenges in quantum computing. Here we report the protection of classical states from environmental bit-flip errors and demonstrate the suppression of these errors with increasing system size. We use a linear array of nine qubits, which is a natural step towards the two-dimensional surface code QEC scheme7, and track errors as they occur by repeatedly performing projective quantum non-demolition parity measurements. Relative to a single physical qubit, we reduce the failure rate in retrieving an input state by a factor of 2.7 when using five of our nine qubits and by a factor of 8.5 when using all nine qubits after eight cycles. Additionally, we tomographically verify preservation of the non-classical Greenberger–Horne–Zeilinger state. The successful suppression of environment-induced errors will motivate further research into the many challenges associated with building a large-scale superconducting quantum computer.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Shor, P. W. Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493–R2496 (1995)
Calderbank, A. R. & Shor, P. W. Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098–1105 (1996)
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996)
Bravyi, S. B. & Kitaev, A. Y. Quantum codes on a lattice with boundary. Preprint at http://arxiv.org/abs/quantph/9811052 (1998)
Raussendorf, R. & Harrington, J. Fault-tolerant quantum computation with high threshold in two dimensions. Phys. Rev. Lett. 98, 190504 (2007)
Raussendorf, R., Harrington, J. & Goyal, K. Topological fault-tolerance in cluster state quantum computation. New J. Phys. 9, 199 (2007)
Fowler, A. G., Mariantoni, M., Martinis, J. M. & Cleland, A. N. Surface codes: towards practical large-scale quantum computation. Phys. Rev. A 86, 032324 (2012)
Cory, D. G. et al. Experimental quantum error correction. Phys. Rev. Lett. 81, 2152–2155 (1998)
Knill, E., Laflamme, R., Martinez, R. & Negrevergne, C. Benchmarking quantum computers: the five qubit error correcting code. Phys. Rev. Lett. 86, 5811–5814 (2001)
Chiaverini, J. et al. Realization of quantum error correction. Nature 432, 602–605 (2004)
Reed, M. et al. Realization of three-qubit quantum error correction with superconducting circuits. Nature 482, 382–385 (2012)
Chow, J. M. et al. Implementing a strand of a scalable fault-tolerant quantum computing fabric. Nature Commun. 5, 4015 (2014)
Riste, D. et al. Detecting bit-flip errors in a logical qubit using stabilizer measurements. Preprint at http://arxiv.org/abs/1411.5542 (2014)
Nigg, D. et al. Quantum computations on a topologically encoded qubit. Science 345, 302–305 (2014)
Córcoles, A. et al. Detecting arbitrary quantum errors via stabilizer measurements on a sublattice of the surface code. Preprint at http://arxiv.org/abs/1410.6419 (2014)
Schindler, P. et al. Experimental repetitive quantum error correction. Science 332, 1059–1061 (2011)
Sun, L. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444–448 (2014)
Bombin, H. & Martin-Delgado, M. Quantum measurements and gates by code deformation. J. Phys. A 42, 095302 (2009)
Barends, R. et al. Superconducting quantum circuits at the surface code threshold for fault tolerance. Nature 508, 500–503 (2014)
Jeffrey, E. et al. Fast accurate state measurement with superconducting qubits. Phys. Rev. Lett. 112, 190504 (2014)
Barends, R. et al. Coherent Josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013)
Fowler, A. G., Sank, D., Kelly, J., Barends, R. & Martinis, J. M. Scalable extraction of error models from the output of error detection circuits. Preprint at http://arxiv.org/abs/1405.1454 (2014)
Edmonds, J. Paths, trees, and flowers. Can. J. Math. 17, 449–467 (1965)
Edmonds, J. Maximum matching and a polyhedron with 0,1-vertices. J. Res. Natl Bur. Stand. B 69, 125–130 (1965)
Fowler, A. G. Minimum weight perfect matching of fault-tolerant topological quantum error correction in average O(1) parallel time. Quant. Inform. Comput. 15, 0145–0158 (2015)
Gühne, O. & Seevinck, M. Separability criteria for genuine multiparticle entanglement. New J. Phys. 12, 053002 (2010)
Harty, T. et al. High-fidelity preparation, gates, memory and readout of a trapped-ion quantum bit. Phys. Rev. Lett. 113, 220501 (2014)
Acknowledgements
We thank A. N. Korotkov and D. L. Moehring for discussions, and P. Duda for help with photomasks and photolithography. This work was supported by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), through Army Research Office grants W911NF-09-1-0375 and W911NF-10-1-0334. All statements of fact, opinion or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of IARPA, the ODNI or the US Government. Devices were made at the UC Santa Barbara Nanofabrication Facility, a part of the US NSF-funded National Nanotechnology Infrastructure Network, and at the NanoStructures Cleanroom Facility.
Author information
Authors and Affiliations
Contributions
J.K. and R.B. designed the sample and performed the experiment. A.G.F. and J.M.M. designed the experiment. J.K., R.B. and A.M. fabricated the sample. A.G.F., J.K. and R.B. analysed the data. J.K., R.B., A.G.F. and J.M.M. co-wrote the manuscript. All authors contributed to the fabrication process, experimental set-up and manuscript preparation.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-31, Supplementary Tables 1-3 and additional references. (PDF 2886 kb)
Rights and permissions
About this article
Cite this article
Kelly, J., Barends, R., Fowler, A. et al. State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015). https://doi.org/10.1038/nature14270
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14270
This article is cited by
-
Fast joint parity measurement via collective interactions induced by stimulated emission
Nature Communications (2024)
-
Autonomous error correction of a single logical qubit using two transmons
Nature Communications (2024)
-
Deterministic Bell state measurement with a single quantum memory
npj Quantum Information (2023)
-
Beating the break-even point with a discrete-variable-encoded logical qubit
Nature (2023)
-
A Review of Developments in Superconducting Quantum Processors
Journal of the Indian Institute of Science (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.