Abstract
Earth’s magnetic field has been thought to arise from thermal convection of molten iron alloy in the outer core, but recent density functional theory calculations have suggested that the conductivity of iron is too high to support thermal convection1,2,3,4, resulting in the investigation of chemically driven convection5,6. These calculations for resistivity were based on electron–phonon scattering. Here we apply self-consistent density functional theory plus dynamical mean-field theory (DFT + DMFT)7 to iron and find that at high temperatures electron–electron scattering is comparable to the electron–phonon scattering, bringing theory into agreement with experiments and solving the transport problem in Earth’s core. The conventional thermal dynamo picture is safe. We find that electron–electron scattering of d electrons is important at high temperatures in transition metals, in contrast to textbook analyses since Mott8,9, and that 4s electron contributions to transport are negligible, in contrast to numerous models used for over fifty years. The DFT+DMFT method should be applicable to other high-temperature systems where electron correlations are important.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Change history
13 April 2016
A Correction to this paper has been published: https://doi.org/10.1038/nature17648
References
Sha, X. & Cohen, R. E. First-principles studies of electrical resistivity of iron under pressure. J. Phys. Condens. Matter 23, 075401 (2011)
de Koker, N., Steinle-Neumann, G. & Vlček, V. Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earth's core. Proc. Natl Acad. Sci. USA 109, 4070–4073 (2012)
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. Thermal and electrical conductivity of iron at Earth's core conditions. Nature 485, 355–358 (2012)
Gomi, H. et al. The high conductivity of iron and thermal evolution of the Earth's core. Phys. Earth Planet. Inter. 224, 88–103 (2013)
Buffett, B. Geomagnetism under scrutiny. Nature 485, 319–320 (2012)
Olson, P. The new core paradox. Science 342, 431–432 (2013)
Haule, K., Yee, C. & Kim, K. Dynamical mean-field theory within the full-potential methods: electronic structure of CeIrIn5, CeCoIn5, and CeRhIn5 . Phys. Rev. B 81, 195107 (2010)
Mott, N. F. Electrons in transition metals. Adv. Phys. 13, 325–422 (1964)
Allen, P. B. Electron transport. Contemp. Concepts Condens. Matter Sci. 2, 165–218 (2006)
Stacey, F. D. & Anderson, O. L. Electrical and thermal conductivities of Fe-Ni-Si alloy under core conditions. Phys. Earth Planet. Inter. 124, 153–162 (2001)
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. Thermal and electrical conductivity of solid iron and iron-silicon mixtures at Earth's core conditions. Earth Planet. Sci. Lett. 393, 159–164 (2014)
Elsasser, W. M. Induction effects in terrestrial magnetism. Part II. The secular variation. Phys. Rev. 70, 202–212 (1946)
Yin, Z. P., Haule, K. & Kotliar, G. Kinetic frustration and the nature of the magnetic and paramagnetic states in iron pnictides and iron chalcogenides. Nature Mater. 10, 932–935 (2011)
Mandal, S., Cohen, R. E. & Haule, K. Strong pressure dependent electron-phonon coupling in FeSe. Phys. Rev. B 89, 220502 (2014)
Keeler, R. N. & Mitchell, A. C. Electrical conductivity, demagnetization, and the high-pressure phase transition in shock-compressed iron. Solid State Commun. 7, 271–274 (1969)
Keeler, R. N. & Royce, E. B. in Physics of High Energy Density (eds Caldirola, P. & Knoepfel, H. ) 106–125 (Proceedings of the International School of Physics Enrico Fermi Vol. 48, 1971)
Bi, Y., Tan, H. & Jing, F. Electrical conductivity of iron under shock compression up to 200 GPa. J. Phys. Condens. Matter 14, 10849–10854 (2002)
Lay, T., Hernlund, J. & Buffett, B. A. Core-mantle boundary heat flow. Nature Geosci. 1, 25–32 (2008)
Wu, B., Driscoll, P. & Olson, P. A statistical boundary layer model for the mantle D″ region. J. Geophys. Res. 116, B12112 (2011)
Tarduno, J. A. et al. Geodynamo, solar wind, and magnetopause 3.4 to 3.45 billion years ago. Science 327, 1238–1240 (2010)
Balchan, A. S. & Drickamer, H. G. High pressure electrical resistance cell, and calibration points above 100 kilobars. Rev. Sci. Instrum. 32, 308 http://dx.doi.org/10.1063/1.1717350 (1961)
Reichlin, R. L. Measuring the electrical resistance of metals to 40 GPa in the diamond-anvil cell. Rev. Sci. Instrum. 54, 1674 http://dx.doi.org/10.1063/1.1137308 (1983)
Seagle, C. T., Cottrell, E., Fei, Y., Hummer, D. R. & Prakapenka, V. B. Electrical and thermal transport properties of iron and iron-silicon alloy at high pressure. Geophys. Res. Lett. 40, 5377–5381 (2013)
Steinle-Neumann, G., Cohen, R. E. & Stixrude, L. Magnetism in iron as a function of pressure. J. Phys. Condens. Matter 16, S1109–S1119 (2004)
Steinle-Neumann, G., Stixrude, L. & Cohen, R. E. Magnetism in dense hexagonal iron. Proc. Natl Acad. Sci. USA 101, 33–36 (2004)
Deng, X. et al. How bad metals turn good: spectroscopic signatures of resilient quasiparticles. Phys. Rev. Lett. 110, 086401 (2013)
Deng, L., Seagle, C., Fei, Y. & Shahar, A. High pressure and temperature electrical resistivity of iron and implications for planetary cores. Geophys. Res. Lett. 40, 33–37 (2013)
Gurvitch, M. & Fiory, A. T. Resistivity of La1. 825Sr0. 175CuO4 and Y Ba2Cu3O7 to 1100 K: absence of saturation and its implications. Phys. Rev. Lett. 59, 1337–1340 (1987)
Xu, W., Haule, K. & Kotliar, G. Hidden Fermi liquid, scattering rate saturation, and Nernst effect: a dynamical mean-field theory perspective. Phys. Rev. Lett. 111, 036401 (2013)
Stixrude, L., Wasserman, E. & Cohen, R. E. Composition and temperature of Earth's inner core. J. Geophys. Res. 102, 24729–24739 (1997)
Sha, X. & Cohen, R. E. First-principles thermal equation of state and thermoelasticity of hcp Fe at high pressures. Phys. Rev. B 81, 094105 (2010)
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996)
Kotliar, G. et al. Electronic structure calculations with dynamical mean-field theory. Rev. Mod. Phys. 78, 865 (2006)
Georges, A., Kotliar, G., Krauth, W. & Rozenberg, M. J. Dynamical mean-field theory of strongly correlated fermion systems and the limit of infinite dimensions. Rev. Mod. Phys. 68, 13 (1996)
Anisimov, V. I., Aryasetiawan, F. & Lichtenstein, A. I. First-principles calculations of the electronic structure and spectra of strongly correlated systems: the LDA+U method. J. Phys. Condens. Matter 9, 767–808 (1997)
Czyżyk, M. T. & Sawatzky, G. A. Local-density functional and on-site correlations: The electronic structure of La2CuO4 and LaCuO3 . Phys. Rev. B 49, 14211 (1994)
Werner, P., Comanac, A., de'Medici, L., Troyer, M. & Millis, A. J. Continuous-time solver for quantum impurity models. Phys. Rev. Lett. 97, 076405 (2006)
Haule, K. Quantum Monte Carlo impurity solver for cluster dynamical mean-field theory and electronic structure calculations with adjustable cluster base. Phys. Rev. B 75, 155113 (2007)
Blaha, P., Schwarz, K., Madsen, G. K. H., Kvasnicka, K. & Luitz, J. in Wien2K (ed. Schwarz, K. ) (Technische Universitat Wien, 2001)
Wu, Z. & Cohen, R. E. More accurate generalized gradient approximation for solids. Phys. Rev. B 73, 235116 (2006)
Blöchl, P. E., Jepsen, O. & Andersen, O. K. Improved tetrahedron method for Brillouin-zone integrations. Phys. Rev. B 49, 16223 (1994)
Sha, X. & Cohen, R. E. Elastic isotropy of ε-Fe under Earth's core conditions. Geophys. Res. Lett. 37, L10302 (2010)
Dziewonski, A. M. & Anderson, D. L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 25, 297–356 (1981)
Sha, X. & Cohen, R. E. Thermal effects on lattice strain in ε-Fe under pressure. Phys. Rev. B 74, 064103 (2006)
Basov, D. N., Averitt, R. D., van der Marel, D., Dressel, M. & Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 83, 471–541 (2011)
Cohen, R. E., Fei, Y., Downs, R., Mazin, I. I. & Isaak, D. G. in High-Pressure Materials Research Materials Research Society Proceedings (eds Wentzcovitch, R., Hemley, R. J., Nellis, W. J. & Yu, P. ) Vol. 499, 27–37 (Materials Research Society, 1998)
Ohta, K. et al. Experimental and theoretical evidence for pressure-induced metallization in FeO with the rock-salt type structure. Phys. Rev. Lett. 108, 026403 (2012)
Shim, J. H., Haule, K. & Kotliar, G. Fluctuating valence in a correlated solid and the anomalous properties of δ-plutonium. Nature 446, 513–516 (2007)
Shim, J. H., Haule, K. & Kotliar, G. Modelling the localized to itinerant electronic transition in the heavy fermion system CeIrIn5 . Science 318, 1615–1617 (2007)
Liu, M. et al. Nature of magnetic excitations in superconducting BaFe1. 9Ni0. 1As2 . Nature Phys. 8, 376 (2012)
Jarrell, M. & Gubernatis, J. E. Bayesian inference and the analytic continuation of imaginary time quantum Monte Carlo data. Phys. Rep. 269, 133–195 (1996)
Pourovskii, L. V. et al. Electronic properties and magnetism of iron at the Earth's inner core conditions. Phys. Rev. B 87, 115130 (2013)
Khurana, A. Electrical conductivity in the infinite-dimensional Hubbard model. Phys. Rev. Lett. 64, 1990 (1990)
Yoo, C. S., Akella, J., Campbell, A. J., Mao, H. K. & Hemley, R. J. Phase diagram of iron by in situ X-ray diffraction: implications for Earth's core. Science 270, 1473–1475 (1995)
Brown, J. M. & McQueen, R. G. Phase transitions, Grüneisen parameter, and elasticity for shocked iron between 77 GPa and 400 GPa. J. Geophys. Res. 91, 7485–7494 (1986)
Nguyen, J. H. & Holmes, N. C. Melting of iron at the physical conditions of the Earth's core. Nature 427, 339–342 (2004)
Acknowledgements
This work is supported by National Science Foundation (NSF) grants EAR-1214807, DMS-1025392, and DMR-1405303. R.E.C. is supported by the Carnegie Institution and the European Research Council Advanced Grant ToMCaT. K.H. is supported by NSF grant DMR-1405303. This research used the NSF Extreme Science and Engineering Discovery Environment (XSEDE) supercomputer ‘Stampede’, and also used the resources of the Oak Ridge Leadership Computing Facility at the Oak Ridge National Laboratory, which is supported by the Office of Science of the US Department of Energy under contract number DE-AC05-00OR22725. R.E.C. and P.Z. thank I. Mazin, S. Labrosse and R. Caracas for discussions. We also acknowledge J. Robb for assistance with the manuscript preparation.
Author information
Authors and Affiliations
Contributions
R.E.C. designed the project, P.Z. performed the computations, P.Z., R.E.C. and K.H. analysed the results and prepared the paper. The DFT + DMFT code was developed by K.H.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
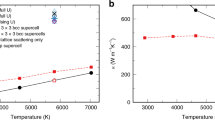
Extended Data Figure 1 Pressure versus temperature relationship of hcp iron at Earth’s core density and along the Hugoniot line31.
The two lines cross at P = 269.9 GPa, T = 6,658 K at Earth’s core density.
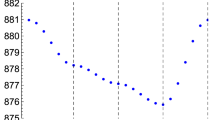
Extended Data Figure 2 Extrapolation of ImΣ(iωn) to zero imaginary frequency.
The self-energy is from the  orbital of hcp iron at Earth’s core density and 6,000 K. Three extrapolation methods are used: linear, cubic spline and Akima spline. The imaginary part of self-energy at i0+ ranges from −0.23 eV to −0.12 eV.
orbital of hcp iron at Earth’s core density and 6,000 K. Three extrapolation methods are used: linear, cubic spline and Akima spline. The imaginary part of self-energy at i0+ ranges from −0.23 eV to −0.12 eV.
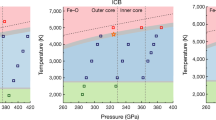
Extended Data Figure 3 The imaginary part of self-energies in real frequency on the  orbital of hcp iron at Earth’s core density and 6,000 K.
orbital of hcp iron at Earth’s core density and 6,000 K.
The self-energies are from three analytic continuation methods: MaxEnt, Padé and singular value decomposition. The inset shows the same imaginary part of self-energies in energy range [−0.01 eV, 0.01 eV] around the Fermi level. The self-energies from three analytic continuation methods agree at the low-energy region.
Rights and permissions
About this article
Cite this article
Zhang, P., Cohen, R. & Haule, K. Effects of electron correlations on transport properties of iron at Earth’s core conditions. Nature 517, 605–607 (2015). https://doi.org/10.1038/nature14090
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature14090
This article is cited by
-
Size-dependent electrical transport properties in Co nanocluster-assembled granular films
Scientific Reports (2017)
-
Saturation of electrical resistivity of solid iron at Earth’s core conditions
SpringerPlus (2016)
-
Magnetic field stretching at the top of the shell of numerical dynamos
Earth, Planets and Space (2016)
-
Powering Earth’s dynamo with magnesium precipitation from the core
Nature (2016)
-
Iron snow, crystal floats, and inner-core growth: modes of core solidification and implications for dynamos in terrestrial planets and moons
Progress in Earth and Planetary Science (2015)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

 orbital of hcp iron at Earth’s core density and 6,000 K.
orbital of hcp iron at Earth’s core density and 6,000 K.