Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Observation of quantized conductance in neutral matter

Nature volume 517, pages 64–67 (2015)Cite this article

Subjects

Abstract

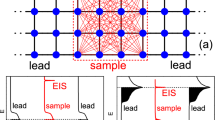
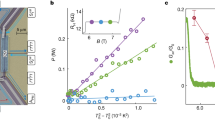
In transport experiments, the quantum nature of matter becomes directly evident when changes in conductance occur only in discrete steps1, with a size determined solely by Planck’s constant h. Observations of quantized steps in electrical conductance2,3 have provided important insights into the physics of mesoscopic systems4 and have allowed the development of quantum electronic devices5. Even though quantized conductance should not rely on the presence of electric charges, it has never been observed for neutral, massive particles6. In its most fundamental form, it requires a quantum-degenerate Fermi gas, a ballistic and adiabatic transport channel, and a constriction with dimensions comparable to the Fermi wavelength. Here we report the observation of quantized conductance in the transport of neutral atoms driven by a chemical potential bias. The atoms are in an ultraballistic regime, where their mean free path exceeds not only the size of the transport channel, but also the size of the entire system, including the atom reservoirs. We use high-resolution lithography to shape light potentials that realize either a quantum point contact or a quantum wire for atoms. These constrictions are imprinted on a quasi-two-dimensional ballistic channel connecting the reservoirs7. By varying either a gate potential or the transverse confinement of the constrictions, we observe distinct plateaux in the atom conductance. The conductance in the first plateau is found to be equal to the universal conductance quantum, 1/h. We use Landauer’s formula to model our results and find good agreement for low gate potentials, with all parameters determined a priori. Our experiment lets us investigate quantum conductors with wide control not only over the channel geometry, but also over the reservoir properties, such as interaction strength, size and thermalization rate.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: An atomic QPC.
Figure 2: Conductance as a function of gate potential.
Figure 3: Conductance as a function of horizontal confinement.
Figure 4: Quantum wire: conductance as a function of gate potential.

Similar content being viewed by others

References

  1. Imry, Y. in Directions in Condensed Matter (eds Grinstein, G. & Mazenko, G. ) 120–145 (World Scientific, 1986)

    Google Scholar 

  2. van Wees, B. J. et al. Quantized conductance of point contacts in a two-dimensional electron gas. Phys. Rev. Lett. 60, 848–850 (1988)

    ADS  CAS  PubMed  Google Scholar 

  3. Wharam, D. A. et al. One-dimensional transport and the quantisation of the ballistic resistance. J. Phys. C 21, L209 (1988)

    Google Scholar 

  4. Imry, Y. Introduction to Mesoscopic Physics (Oxford Univ. Press, 2002)

    Google Scholar 

  5. Ihn, T. Semiconductor Nanostructures (Oxford Univ. Press, 2010)

    Google Scholar 

  6. Sato, Y., Eom, B.-H. & Packard, R. On the feasibility of detecting quantized conductance in neutral matter. J. Low Temp. Phys. 141, 99–109 (2005)

    ADS  CAS  Google Scholar 

  7. Brantut, J.-P., Meineke, J., Stadler, D., Krinner, S. & Esslinger, T. Conduction of ultracold fermions through a mesoscopic channel. Science 337, 1069–1071 (2012)

    ADS  CAS  PubMed  Google Scholar 

  8. Landauer, R. Spatial variation of currents and fields due to localized scatterers in metallic conduction. IBM J. Res. Develop. 1, 223–231 (1957)

    MathSciNet  Google Scholar 

  9. Büttiker, M., Imry, Y., Landauer, R. & Pinhas, S. Generalized many-channel conductance formula with application to small rings. Phys. Rev. B 31, 6207–6215 (1985)

    ADS  Google Scholar 

  10. Krans, J. M., van Ruitenbeek, J. M., Fisun, V. V., Yanson, I. K. & de Jongh, L. J. The signature of conductance quantization in metallic point contacts. Nature 375, 767–769 (1995)

    ADS  CAS  Google Scholar 

  11. Frank, S., Poncharal, P., Wang, Z. L. & de Heer, W. A. Carbon nanotube quantum resistors. Science 280, 1744–1746 (1998)

    ADS  CAS  PubMed  Google Scholar 

  12. Thywissen, J. H., Westervelt, R. M. & Prentiss, M. Quantum point contacts for neutral atoms. Phys. Rev. Lett. 83, 3762–3765 (1999)

    ADS  CAS  Google Scholar 

  13. Görlitz, A. et al. Realization of Bose-Einstein condensates in lower dimensions. Phys. Rev. Lett. 87, 130402 (2001)

    ADS  PubMed  Google Scholar 

  14. Moritz, H., Stöferle, T., Köhl, M. & Esslinger, T. Exciting collective oscillations in a trapped 1D gas. Phys. Rev. Lett. 91, 250402 (2003)

    ADS  PubMed  Google Scholar 

  15. Paredes, B. et al. Tonks–Girardeau gas of ultracold atoms in an optical lattice. Nature 429, 277–281 (2004)

    ADS  CAS  PubMed  Google Scholar 

  16. Kinoshita, T., Wenger, T. & Weiss, D. S. Observation of a one-dimensional Tonks-Girardeau gas. Science 305, 1125–1128 (2004)

    ADS  CAS  PubMed  Google Scholar 

  17. Bouchoule, I., van Druten, N. & Westbrook, C. in Atom Chips (eds Reichel, J. & Vuletic, V. ) 331–363 (Wiley, 2010)

    Google Scholar 

  18. Serwane, F. et al. Deterministic preparation of a tunable few-fermion system. Science 332, 336–338 (2011)

    ADS  CAS  PubMed  Google Scholar 

  19. Albiez, M. et al. Direct observation of tunneling and nonlinear self-trapping in a single bosonic Josephson junction. Phys. Rev. Lett. 95, 010402 (2005)

    ADS  PubMed  Google Scholar 

  20. Stadler, D., Krinner, S., Meineke, J., Brantut, J.-P. & Esslinger, T. Observing the drop of resistance in the flow of a superfluid Fermi gas. Nature 491, 736–739 (2012)

    ADS  CAS  PubMed  Google Scholar 

  21. Krinner, S., Stadler, D., Meineke, J., Brantut, J.-P. & Esslinger, T. Superfluidity with disorder in a thin film of quantum gas. Phys. Rev. Lett. 110, 100601 (2013)

    ADS  PubMed  Google Scholar 

  22. van Houten, H. & Beenakker, C. Quantum point contacts. Phys. Today 49, 22–27 (1996)

    CAS  Google Scholar 

  23. Zimmermann, B., Müller, T., Meineke, J., Esslinger, T. & Moritz, H. High-resolution imaging of ultracold fermions in microscopically tailored optical potentials. New J. Phys. 13, 043007 (2011)

    ADS  Google Scholar 

  24. Glazman, L. I. & Lesovik, G. B. Khmel’Nitskiǐ, D. E. & Shekhter, R. I. Reflectionless quantum transport and fundamental ballistic-resistance steps in microscopic constrictions. JETP Lett. 48, 238–241 (1988)

    ADS  Google Scholar 

  25. Kouwenhoven, L. P. et al. Nonlinear conductance of quantum point contacts. Phys. Rev. B 39, 8040–8043 (1989)

    ADS  CAS  Google Scholar 

  26. Ulreich, S. & Zwerger, W. Where is the potential drop in a quantum point contact? Superlattices Microstruct. 23, 719–730 (1998)

    ADS  Google Scholar 

  27. Szafer, A. & Stone, A. D. Theory of quantum conduction through a constriction. Phys. Rev. Lett. 62, 300–303 (1989)

    ADS  CAS  PubMed  Google Scholar 

  28. Yacoby, A. & Imry, Y. Quantization of the conductance of ballistic point contacts beyond the adiabatic approximation. Phys. Rev. B 41, 5341–5350 (1990)

    ADS  CAS  Google Scholar 

  29. Vignale, G. & Di Ventra, M. Incompleteness of the Landauer formula for electronic transport. Phys. Rev. B 79, 014201 (2009)

    ADS  Google Scholar 

  30. Hasan, M. Z. & Kane, C. L. Topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010)

    ADS  CAS  Google Scholar 

  31. Sachdev, S. Quantum Phase Transitions 260–290 (Cambridge Univ. Press, 2011)

    MATH  Google Scholar 

  32. Lee, P. A. & Stone, A. D. Universal conductance fluctuations in metals. Phys. Rev. Lett. 55, 1622 (1985)

    ADS  CAS  PubMed  Google Scholar 

  33. Brantut, J.-P. et al. A thermoelectric heat engine with ultracold atoms. Science 342, 713–715 (2013)

    ADS  CAS  PubMed  Google Scholar 

  34. Hung, C.-L., Zhang, X., Gemelke, N. & Chin, C. Accelerating evaporative cooling of atoms into Bose-Einstein condensation in optical traps. Phys. Rev. A 78, 011604 (2008)

    ADS  Google Scholar 

  35. Beria, M., Iqbal, Y., Di Ventra, M. & Müller, M. Quantum-statistics-induced flow patterns in driven ideal Fermi gases. Phys. Rev. A 88, 043611 (2013)

    ADS  Google Scholar 

  36. Gattobigio, G. L., Couvert, A., Georgeot, B. & Guéry-Odelin, D. Exploring classically chaotic potentials with a matter wave quantum probe. Phys. Rev. Lett. 107, 254104 (2011)

    ADS  CAS  PubMed  Google Scholar 

  37. O’Hara, K. M., Gehm, M. E., Granade, S. R. & Thomas, J. E. Scaling laws for evaporative cooling in time-dependent optical traps. Phys. Rev. A 64, 051403 (2001)

    ADS  Google Scholar 

  38. Du, X., Zhang, Y. & Thomas, J. E. Inelastic collisions of a fermi gas in the BEC-BCS crossover. Phys. Rev. Lett. 102, 250402 (2009)

    ADS  CAS  PubMed  Google Scholar 

  39. Zürn, G. et al. Precise characterization of Li6 Feshbach resonances using trap-sideband-resolved RF spectroscopy of weakly bound molecules. Phys. Rev. Lett. 110, 135301 (2013)

    ADS  PubMed  Google Scholar 

  40. Migdal, A. Qualitative Methods in Quantum Theory 115–118 (Perseus, 2000)

    Google Scholar 

  41. Büttiker, M. Role of quantum coherence in series resistors. Phys. Rev. B 33, 3020–3026 (1986)

    ADS  Google Scholar 

  42. Ulreich, S. Transport Durch Ballistische Leiter 44–52, PhD thesis, LMU München. (1997)

Download references

Acknowledgements

We acknowledge discussions with G. Blatter, K. Ensslin, C. Glattli, T. Giamarchi, C. Grenier and M. Lebrat, and thank C. Chin, T. Ihn, Y. Imry, and W. Zwerger for their careful reading of the manuscript and for discussions. We acknowledge financing from NCCR QSIT, the ERC Project SQMS, the FP7 project SIQS and ETHZ. J.-P.B. is supported by the Ambizione program of SNF.

Author information

Authors and Affiliations

  1. Institute for Quantum Electronics, ETH Zurich, 8093 Zurich, Switzerland ,

    Sebastian Krinner, David Stadler, Dominik Husmann, Jean-Philippe Brantut & Tilman Esslinger

Authors
  1. Sebastian Krinner
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. David Stadler
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Dominik Husmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jean-Philippe Brantut
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Tilman Esslinger
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

All authors contributed equally to this work.

Corresponding author

Correspondence to Jean-Philippe Brantut.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Extended data figures and tables

Extended Data Figure 1 Distribution of timescales in the reservoirs.

The corresponding physical phenomena are indicated on the time line. The meanings of the different notations are defined in the text.

Extended Data Figure 2 Conductance as a function of gate potential for non-interacting reservoirs.

Filled magenta squares correspond to a scattering length of a = −4a0, whereas open blue circles represent a reference data set for weakly interacting reservoirs, where a = −187a0. Each data point is the mean of nine measurements, and error bars indicate one standard deviation. The black line is a theoretical prediction based on the Landauer formula of conductance, and the shaded region reflects the uncertainties in the input parameters.

Source data

Extended Data Figure 3 Illustration of the adiabaticity criterion.

Transverse energy level spacing Δωx = ΔEx /h along the tightly confined QPC direction (solid red line), and corresponding temporal change in the ground-state trapping frequency in the moving frame of the atoms as a function of position along the QPC for the three possible values of nz when q = 3 modes are populated.

Extended Data Figure 4 Conductance of the 2D region and of the QPC as a function of gate potential.

a, Conductance G2D as a function of gate potential in the absence of the QPC. The solid line is a linear fit to the data. b, Conductance GQPC of the QPC only, when considering the contact resistances of the 2D confinement as series resistors to the QPC. The data set, colour code, solid line and shaded region are the same as in Extended Data Fig. 2. Error bars are obtained by propagating the errors in G and G2D.

Source data

PowerPoint slides

Source data

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Krinner, S., Stadler, D., Husmann, D. et al. Observation of quantized conductance in neutral matter. Nature 517, 64–67 (2015). https://doi.org/10.1038/nature14049

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature14049

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing