Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Ramp compression of diamond to five terapascals

Nature volume 511, pages 330–333 (2014)Cite this article

Subjects

Abstract

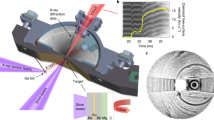
The recent discovery of more than a thousand planets outside our Solar System1,2, together with the significant push to achieve inertially confined fusion in the laboratory3, has prompted a renewed interest in how dense matter behaves at millions to billions of atmospheres of pressure. The theoretical description of such electron-degenerate matter has matured since the early quantum statistical model of Thomas and Fermi4,5,6,7,8,9,10, and now suggests that new complexities can emerge at pressures where core electrons (not only valence electrons) influence the structure and bonding of matter11. Recent developments in shock-free dynamic (ramp) compression now allow laboratory access to this dense matter regime. Here we describe ramp-compression measurements for diamond, achieving 3.7-fold compression at a peak pressure of 5 terapascals (equivalent to 50 million atmospheres). These equation-of-state data can now be compared to first-principles density functional calculations12 and theories long used to describe matter present in the interiors of giant planets, in stars, and in inertial-confinement fusion experiments. Our data also provide new constraints on mass–radius relationships for carbon-rich planets.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Velocity interferometry for ramp compressed diamond.
Figure 2: Ramp compression stress and sound velocity measurements.
Figure 3: Mass–radius relationships for homogenous-composition planets.

References

  1. Schneider, J., Dedieu, C., Le Sidaner, P., Savalle, R. & Zolotukhin, I. Defining and cataloging exoplanets: the exoplanet.eu database. Astron. Astrophys. 532, A79 (2011)

    Article  ADS  Google Scholar 

  2. Seager, S., Kuchner, M., Hier-Majumder, C. A. & Militzer, B. Mass-radius relationships for solid exoplanets. Astrophys. J. 669, 1279–1297 (2007)

    Article  CAS  ADS  Google Scholar 

  3. Edwards, M. J. et al. Progress towards ignition on the National Ignition Facility. Phys. Plasmas 20, 070501 (2013)

    Article  ADS  Google Scholar 

  4. Thomas, L. H. The calculation of atomic fields. Math. Proc. Camb. Phil. Soc. 23, 542–548 (1927)

    Article  CAS  ADS  Google Scholar 

  5. Dirac, P. A. M. Note on exchange phenomena in the Thomas atom. Math. Proc. Camb. Phil. Soc. 26, 376–385 (1930)

    Article  CAS  ADS  Google Scholar 

  6. Feynman, R. P., Metropolis, N. & Teller, E. Equation of state of elements based on the generalized Fermi-Thomas theory. Phys. Rev. 75, 1561–1573 (1949)

    Article  CAS  ADS  Google Scholar 

  7. Salpeter, E. E. & Zapolsky, H. S. Theoretical high pressure equations of state, including correlation energy. Phys. Rev. 158, 876–886 (1967)

    Article  CAS  ADS  Google Scholar 

  8. Abrahams, A. M. & Shapiro, S. L. Cold equation of state from Thomas-Fermi-Dirac-Weizsacker theory. Phys. Rev. A 42, 2530–2538 (1990)

    Article  CAS  ADS  Google Scholar 

  9. Lai, D., Abrahams, A. M. & Shapiro, S. L. Equation of state in metals and cold stars: evaluation of statistical models. Astrophys. J. 377, 612–628 (1991)

    Article  ADS  Google Scholar 

  10. Correa, A. A., Benedict, L. X., Young, D. A., Schwegler, E. & Bonev, S. A. A first principles multi-phase equation of state of carbon under extreme conditions. Phys. Rev. B 78, 024101 (2008)

    Article  ADS  Google Scholar 

  11. Neaton, J. B. & Ashcroft, N. W. Pairing in dense lithium. Nature 400, 141–144 (1999)

    Article  CAS  ADS  Google Scholar 

  12. Martinez-Canales, M., Pickard, C. J. & Needs, R. J. Theormodynamically stable phase of carbon at multiterapascal pressures. Phys. Rev. Lett. 108, 045704 (2012)

    Article  ADS  Google Scholar 

  13. Swift, D. C. et al. Mass-radius relationships for exoplanets. Astrophys. J. 744, 59–68 (2012)

    Article  ADS  Google Scholar 

  14. Dubrovinsky, L., Dubrovinskaia, N., Prakapenka, V. B. & Abakumov, A. M. Implementation of micro-ball nanodiamond anvils for high-pressure studies above 6 Mbar. Nature Commun. 3, 1163 (2012)

    Article  ADS  Google Scholar 

  15. Zel’dovich, B. & Raizer, P. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena (Dover, 2002)

    Google Scholar 

  16. Atzeni, S. & Meyer-ter-Vehn, J. The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter (Oxford Univ. Press, 2004)

    Book  Google Scholar 

  17. Rothman, S. D. et al. Measurement of the principle isentropes of lead and lead-antimony alloy to ∼400 kbar by quasi-isentropic compression. J. Phys. D 38, 733–740 (2005)

    Article  CAS  ADS  Google Scholar 

  18. McWilliams, R. S. et al. Strength effects in diamond under shock compression from 0.1 to 1 TPa. Phys. Rev. B 81, 014111 (2010)

    Article  ADS  Google Scholar 

  19. Vinet, P., Ferrante, J., Rose, J. H. & Smith, J. R. Compressibility of solids. J. Geophys. Res. 92, 9319–9325 (1987)

    Article  CAS  ADS  Google Scholar 

  20. Birch, F. Finite elastic strain of cubic crystals. Phys. Rev. 71, 809–824 (1947)

    Article  CAS  ADS  Google Scholar 

  21. Dewaele, A., Datchi, F., Loubeyre, P. & Mezouar, M. High pressure-high temperature equation of state of neon and diamond. Phys. Rev. B 77, 094106 (2008)

    Article  ADS  Google Scholar 

  22. Occelli, F., Loubeyre, P. & Letoullec, R. Properties of diamond under hydrostatic pressures up to 140 GPa. Nature Mater. 2, 151–154 (2003)

    Article  CAS  ADS  Google Scholar 

  23. Smith, R. F. et al. Time-dependence of the alpha to epsilon phase transformation in iron. J. Appl. Phys. 114, 223507 (2013)

    Article  ADS  Google Scholar 

  24. Coppari, F. et al. Experimental evidence for a phase transition in magnesium oxide at exoplanet pressures. Nature Geosci. 6, 926–929 (2013)

    Article  CAS  ADS  Google Scholar 

  25. Sun, J., Klug, D. D. & Martoňák, R. Structural transformations in carbon under extreme pressure: beyond diamond. J. Chem. Phys. 130, 194512 (2009)

    Article  ADS  Google Scholar 

  26. Eggert, J. H. et al. Melting temperature of diamond at ultrahigh pressure. Nature Phys. 6, 40–43 (2010)

    Article  CAS  ADS  Google Scholar 

  27. Madhusudhan, N., Lee, K. K. M. & Mousis, O. A possible carbon-rich interior in super-Earth 55 Cancri e. Astrophys. J. 759, L40 (2012)

    Article  ADS  Google Scholar 

  28. Nettelmann, N. et al. Ab initio equation of state data for hydrogen, helium, and water and the internal structure of Jupiter. Astrophys. J. 683, 1217–1228 (2008)

    Article  CAS  ADS  Google Scholar 

  29. Bailes, M. et al. Transformation of a star into a planet in the millisecond Pulsar binary. Science 333, 1717–1720 (2011)

    Article  CAS  ADS  Google Scholar 

  30. Wagner, F. W., Sohl, F., Hussmann, H., Grott, M. & Rauer, H. Interior structure models of solid exoplanets using material laws in the infinite pressure limit. Icarus 214, 366–376 (2011)

    Article  ADS  Google Scholar 

  31. Eremets, M. I. et al. The strength of diamond. Appl. Phys. Lett. 87, 141902 (2005)

    Article  ADS  Google Scholar 

  32. Bradley, D. K. et al. Diamond at 800 GPa. Phys. Rev. Lett. 102, 075503 (2009)

    Article  CAS  ADS  Google Scholar 

  33. Reichart, P. et al. Three-dimensional hydrogen microscopy in diamond. Science 306, 1537–1540 (2004)

    Article  CAS  ADS  Google Scholar 

  34. Dawedeit, C. et al. Grain size dependent physical and chemical properties of thick CVD diamond films for high energy density physics experiments. Diamond Rel. Mater. 40, 75–81 (2013)

    Article  CAS  ADS  Google Scholar 

  35. Celliers, P. M. et al. Line-imaging velocimeter for shock diagnostics at the Omega laser facility. Rev. Sci. Instrum. 75, 4916–4929 (2004)

    Article  CAS  ADS  Google Scholar 

  36. Aidun, J. B. & Gupta, Y. M. Analysis of Lagrangian gauge measurements of simple and nonsimple plane waves. J. Appl. Phys. 69, 6998–7014 (1991)

    Article  ADS  Google Scholar 

  37. Knudson, M. D., Desjarlais, M. P. & Dolan, D. H. Shock-wave exploration of the high-pressure phases of carbon. Science 322, 1822–1825 (2008)

    Article  CAS  ADS  Google Scholar 

  38. Nagao, H. et al. Hugoniot measurement of diamond under laser shock compression up to 2 TPa. Phys. Plasmas 13, 052705 (2006)

    Article  ADS  Google Scholar 

  39. Brygoo, S. et al. Laser-shock compression of diamond and evidence of a negative-slope melting curve. Nature Mater. 6, 274–277 (2007)

    Article  CAS  ADS  Google Scholar 

  40. Hicks, D. G. et al. High-precision measurements of the diamond Hugoniot in and above the melt region. Phys. Rev. B 78, 174102 (2008)

    Article  ADS  Google Scholar 

  41. McQueen, R. G., Marsh, S. P., Taylor, J. W., Fritz, J. N. & Carter, W. J. in High Velocity Impact Phenomena Ch. 7, 293–417 (Academic Press, 1970)

    Book  Google Scholar 

  42. Herrmann, W. Constitutive equation for the dynamic compaction of ductile porous materials. J. Appl. Phys. 40, 2490–2499 (1969)

    Article  ADS  Google Scholar 

  43. Carroll, M. M. & Holt, A. C. Static and dynamic pore-collapse relations for ductile porous materials. J. Appl. Phys. 43, 1626–1636 (1972)

    Article  ADS  Google Scholar 

  44. Reisman, D. B., Wolfer, W. G., Elsholz, A. & Furnish, M. D. Isentropic compression of irradiated stainless steel on the Z accelerator. J. Appl. Phys. 93, 8952–8957 (2003)

    Article  CAS  ADS  Google Scholar 

  45. Celliers, P. M. et al. Systematic uncertainties in shock-wave impedance-match analysis and the high-pressure equation of state of Al. J. Appl. Phys. 98, 113529 (2005)

    Article  ADS  Google Scholar 

  46. Knudson, M. D. & Desjarlais, M. P. Adiabatic release measurements in α-quartz between 300 and 1200 GPa: characterization of α-quartz as a shock standard in the multimegabar regime. Phys. Rev. B 88, 184107 (2013)

    Article  ADS  Google Scholar 

  47. Hicks, D. G. et al. Shock compression of quartz in the high-pressure fluid regime. Phys. Plasmas 12, 082702 (2005)

    Article  ADS  Google Scholar 

  48. Benedict, L. X. et al. A multiphase equation of state for carbon addressing high pressures and temperatures. Preprint at http://arxiv.org/abs/1311.4577 (2013)

  49. Holzapfel, W. Equations of state for ideal and real solids under strong compression. Europhys. Lett. 16, 67 (1991)

    Article  CAS  ADS  Google Scholar 

Download references

Acknowledgements

We thank the NIF staff, B. Goldstein, Ed Moses, C. Keane, the Science Use of NIF programme, C. Wild (Fraunhofer Institute for Applied Solid-State Physics, Freiburg, Germany) for preparation of the diamond targets, D. Hicks for his analysis work, and M. Millot for reanalysing published diamond Hugoniot data. This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under contract number DE-AC52-07NA27344, with additional support from the Department of Energy, the University of California, and the Miller Institute for Basic Research in Science.

Author information

Authors and Affiliations

  1. Lawrence Livermore National Laboratory, PO Box 808, Livermore, 94550, California, USA

    R. F. Smith, J. H. Eggert, D. G. Braun, J. R. Patterson, R. E. Rudd, J. Biener, A. E. Lazicki, A. V. Hamza, T. Braun, L. X. Benedict, P. M. Celliers & G. W. Collins

  2. Department of Earth and Planetary Science, Department of Astronomy and Miller Institute for Basic Research in Science, University of California, Berkeley, 94720, California, USA

    R. Jeanloz & J. Wang

  3. Department of Geosciences, Princeton University, Princeton, 08544, New Jersey, USA

    T. S. Duffy

Authors
  1. R. F. Smith
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. H. Eggert
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. Jeanloz
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. T. S. Duffy
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. D. G. Braun
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. J. R. Patterson
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. R. E. Rudd
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. J. Biener
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. A. E. Lazicki
    View author publications

    You can also search for this author in PubMed Google Scholar

  10. A. V. Hamza
    View author publications

    You can also search for this author in PubMed Google Scholar

  11. J. Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  12. T. Braun
    View author publications

    You can also search for this author in PubMed Google Scholar

  13. L. X. Benedict
    View author publications

    You can also search for this author in PubMed Google Scholar

  14. P. M. Celliers
    View author publications

    You can also search for this author in PubMed Google Scholar

  15. G. W. Collins
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

R.F.S., J.H.E., D.G.B., P.M.C., J.R.P., A.E.L. and G.W.C. designed, executed and analysed the data from the ramp compression experiments. J.H.E., R.E.R., L.X.B., R.J., T.S.D., J.W. and G.W.C. performed the comparisons of experimental data to EOS models and theory. J.B., T.B. and A.V.H. were instrumental in procuring and metrologizing the diamond step samples.

Corresponding author

Correspondence to G. W. Collins.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Extended data figures and tables

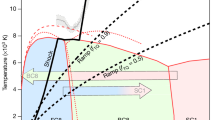
Extended Data Figure 1 Ramp-compressed diamond stress versus density compared to other high-pressure data.

NIF ramp-compression data with 1σ error bars (solid blue line) together with calculated Hugoniots (low-initial-density diamond, solid red line; standard-initial-density diamond, dotted red line) and the calculated cold curve (dashed red line)12 from DFT; a simple Mie–Grüneisen model reduction of Hugoniot data to produce an extrapolated Hugoniot (low-initial-density diamond, solid orange line; standard-initial-density diamond, dotted orange line), and cold curve (dashed orange line); Vinet19 (dot-dashed grey line), Birch-Murnaghan20 (dashed grey line), and Holzapfel49 (dotted grey line) extrapolations of 300-K diamond anvil cell data21,22. The shaded regions show the range of different models for cold curve (grey) and Hugoniot (orange) showing roughly the range of uncertainty in this ultrahigh-pressure regime. Also shown are data from shock experiments (yellow circles37, up triangles38, open pentagons (which used an Al or Mo standard)40, down triangles39, blue pentagons (which used the more accurate quartz standard)40, open squares18), isothermal static data (green circles are ruby-corrected data21,22) and the ramp-compression data of Bradley32 (solid grey line). The ramp-compression data of Bradley used full-density diamond and did not use an initial shock as in NIF data. The inset shows the calculated stress–density relations of the three NIF shots: N110308, N110516 and N110524, showing the level of repeatability between experiments.

Extended Data Table 1 Ramp-compressed diamond stress–density data
Full size table

PowerPoint slides

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Smith, R., Eggert, J., Jeanloz, R. et al. Ramp compression of diamond to five terapascals. Nature 511, 330–333 (2014). https://doi.org/10.1038/nature13526

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature13526

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing