Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Quasiparticle engineering and entanglement propagation in a quantum many-body system

Nature volume 511, pages 202–205 (2014)Cite this article

Subjects

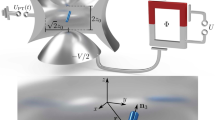
Abstract

The key to explaining and controlling a range of quantum phenomena is to study how information propagates around many-body systems. Quantum dynamics can be described by particle-like carriers of information that emerge in the collective behaviour of the underlying system, the so-called quasiparticles1. These elementary excitations are predicted to distribute quantum information in a fashion determined by the system’s interactions2. Here we report quasiparticle dynamics observed in a quantum many-body system of trapped atomic ions3,4. First, we observe the entanglement distributed by quasiparticles as they trace out light-cone-like wavefronts5,6,7,8,9,10,11. Second, using the ability to tune the interaction range in our system, we observe information propagation in an experimental regime where the effective-light-cone picture does not apply7,12. Our results will enable experimental studies of a range of quantum phenomena, including transport13,14, thermalization15, localization16 and entanglement growth17, and represent a first step towards a new quantum-optic regime of engineered quasiparticles with tunable nonlinear interactions.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Quantum dynamics in a one-dimensional spin chain following a local quench.
Figure 2: Measured quantum dynamics in a seven-ion system following local and global quenches.
Figure 3: Entanglement distribution following a local quench.
Figure 4: Measured quantum dynamics for increasing spin–spin interaction ranges.

References

  1. Sachdev, S. Quantum criticality: competing ground states in low dimensions. Science 288, 475–480 (2000)

    Article  ADS  CAS  Google Scholar 

  2. Calabrese, P. & Cardy, J. Time-dependence of correlation functions following a quantum quench. Phys. Rev. Lett. 96, 136801 (2006)

    Article  ADS  Google Scholar 

  3. Porras, D. & Cirac, J. I. Effective quantum spin systems with trapped ions. Phys. Rev. Lett. 92, 207901 (2004)

    Article  ADS  CAS  Google Scholar 

  4. Friedenauer, H., Schmitz, H., Glueckert, J., Porras, D. & Schaetz, T. Simulating a quantum magnet with trapped ions. Nature Phys. 4, 757–761 (2008)

    Article  ADS  CAS  Google Scholar 

  5. Lieb, E. & Robinson, D. The finite group velocity of quantum spin systems. Commun. Math. Phys. 28, 251–257 (1972)

    Article  ADS  MathSciNet  Google Scholar 

  6. Cramer, M., Serafini, A. & Eisert, J. in Quantum Information and Many Body Quantum Systems (eds Ericsson, M. & Montangero, S. ) 51 (Edizioni della Normale, 2008)

    Google Scholar 

  7. Hastings, M. B. in Quantum Theory from Small to Large Scales, Lecture Notes of the Les Houches Summer School (eds Frohlich, J., Salmhofer, M., Mastropietro, V., Roeck, W. D. & Cugliandolo, L. ) Vol. 95, Ch. 5 (Oxford Univ. Press, 2010)

    Google Scholar 

  8. Nachtergaele, B. & Sims, R. Much ado about something: why Lieb-Robinson bounds are useful. IAMP News Bull. 22–29. (October 2010)

  9. Cheneau, M. et al. Light-cone-like spreading of correlations in a quantum many-body system. Nature 481, 484–487 (2012)

    Article  ADS  CAS  Google Scholar 

  10. Fukuhara, T. et al. Microscopic observation of magnon bound states and their dynamics. Nature 502, 76–79 (2013)

    Article  ADS  CAS  Google Scholar 

  11. Langen, T., Geiger, R., Kuhnert, M., Rauer, B. & Schmiedmayer, J. Local emergence of thermal correlations in an isolated quantum many-body system. Nature Phys. 9, 640–643 (2013)

    Article  ADS  CAS  Google Scholar 

  12. Hauke, P. & Tagliacozzo, L. Spread of correlations in long-range interacting quantum systems. Phys. Rev. Lett. 111, 207202 (2013)

    Article  ADS  CAS  Google Scholar 

  13. Bose, S. Quantum communication through spin chain dynamics: an introductory overview. Contemp. Phys. 48, 13–30 (2007)

    Article  ADS  CAS  Google Scholar 

  14. Rebentrost, P., Mohseni, M., Kassal, I., Lloyd, S. & Aspuru-Guzik, A. Environment-assisted quantum transport. New J. Phys. 11, 033003 (2009)

    Article  ADS  Google Scholar 

  15. Rigol, M., Dunjko, V., Yurovsky, V. & Olshanii, M. Relaxation in a completely integrable many-body quantum system: an ab initio study of the dynamics of the highly excited states of 1D lattice hard-core bosons. Phys. Rev. Lett. 98, 050405 (2007)

    Article  ADS  Google Scholar 

  16. Yao, N. Y. et al. Many-body localization with dipoles. Preprint at http://arXiv.org/abs/1311.7151 (2014)

  17. Schachenmayer, J., Lanyon, B. P., Roos, C. F. & Daley, A. J. Entanglement growth in quench dynamics with variable range interactions. Phys. Rev. X 3, 031015 (2013)

    CAS  Google Scholar 

  18. Kitaev, A. Fault-tolerant quantum computation by anyons. Ann. Phys. 303, 2–30 (2003)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  19. Bravyi, S., Hastings, M. B. & Verstraete, F. Lieb-Robinson bounds and the generation of correlations and topological quantum order. Phys. Rev. Lett. 97, 050401 (2006)

    Article  ADS  CAS  Google Scholar 

  20. Eisert, J. & Osborne, T. General entanglement scaling laws from time evolution. Phys. Rev. Lett. 97, 150404 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  21. Jünemann, J., Cadarso, A., Perez-Garcia, D., Bermudez, A. & Garcia-Ripoll, J. Lieb- Robinson bounds for spin-boson lattice models and trapped ions. Phys. Rev. Lett. 111, 230404 (2013)

    Article  ADS  Google Scholar 

  22. Eisert, J., van den Worm, M., Manmana, S. R. & Kastner, M. Breakdown of quasi-locality in long-range quantum lattice models. Phys. Rev. Lett. 111, 260401 (2013)

    Article  ADS  Google Scholar 

  23. Kim, K. et al. Entanglement and tunable spin-spin couplings between trapped ions using multiple transverse modes. Phys. Rev. Lett. 103, 120502 (2009)

    Article  ADS  CAS  Google Scholar 

  24. Britton, J. W. et al. Engineered two-dimensional Ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 484, 489–492 (2012)

    Article  ADS  CAS  Google Scholar 

  25. Islam, R. et al. Emergence and frustration of magnetism with variable-range interactions in a quantum simulator. Science 340, 583–587 (2013)

    Article  ADS  CAS  Google Scholar 

  26. Richerme, P. et al. Non-local propagation of correlations in long-range interacting quantum systems. Nature http://dx.doi.org/10.1038/nature13450 (this issue)

  27. Plenio, M. B. & Huelga, S. F. Dephasing-assisted transport: quantum networks and biomolecules. New J. Phys. 10, 113019 (2008)

    Article  ADS  Google Scholar 

  28. Gong, Z.-X. & Duan, L.-M. Prethermalization and dynamical transition in an isolated trapped ion spin chain. New J. Phys. 15, 113051 (2013)

    Article  ADS  Google Scholar 

  29. Schindler, P. et al. A quantum information processor with trapped ions. New J. Phys. 15, 123012 (2013)

    Article  ADS  Google Scholar 

  30. Roos, C. F. et al. Bell states of atoms with ultralong lifetimes and their tomographic state analysis. Phys. Rev. Lett. 92, 220402 (2004)

    Article  ADS  CAS  Google Scholar 

  31. Holstein, T. & Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 58, 1098–1113 (1940)

    Article  ADS  Google Scholar 

  32. Sørensen, A. & Mølmer, K. Quantum computation with ions in thermal motion. Phys. Rev. Lett. 82, 1971–1974 (1999)

    Article  ADS  Google Scholar 

  33. Häffner, H. et al. Precision measurement and compensation of optical Stark shifts for an ion-trap quantum processor. Phys. Rev. Lett. 90, 143602 (2003)

    Article  ADS  Google Scholar 

  34. James, D. F. V., Kwiat, P. G., Munro, W. J. & White, A. G. Measurement of qubits. Phys. Rev. A 64, 052312 (2001)

    Article  ADS  Google Scholar 

  35. Wootters, W. K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 80, 2245–2248 (1998)

    Article  ADS  CAS  Google Scholar 

  36. Hastings, M. B. Lieb-Schultz-Mattis in higher dimensions. Phys. Rev. B 69, 104431 (2004)

    Article  ADS  Google Scholar 

  37. Nachtergaele, B. & Sims, R. Lieb-Robinson bounds and the exponential clustering theorem. Commun. Math. Phys. 265, 119–130 (2006)

    Article  ADS  MathSciNet  Google Scholar 

Download references

Acknowledgements

We acknowledge discussions with L. Tagliacozzo, M. Heyl, A. Gorshkov and S. Bose. This work was supported by the Austrian Science Fund (FWF) under grant number P25354-N20, and by the European Commission via the integrated project SIQS and by the Institut für Quanteninformation. We also acknowledge support from the European Research Council through the CRYTERION Project (number 227959).

Author information

Author notes

  1. P. Jurcevic and B. P. Lanyon: These authors contributed equally to this work.

Authors and Affiliations

  1. Institut für Quantenoptik und Quanteninformation, Österreichische Akademie der Wissenschaften, Technikerstraße 21a, 6020 Innsbruck, Austria,

    P. Jurcevic, B. P. Lanyon, P. Hauke, C. Hempel, P. Zoller, R. Blatt & C. F. Roos

  2. Institut für Experimentalphysik, Universität Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria,

    P. Jurcevic, B. P. Lanyon, C. Hempel, R. Blatt & C. F. Roos

  3. Institut für Theoretische Physik, Universität Innsbruck, Technikerstraße 25, 6020 Innsbruck, Austria,

    P. Hauke & P. Zoller

Authors
  1. P. Jurcevic
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. B. P. Lanyon
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. P. Hauke
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. C. Hempel
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. P. Zoller
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. R. Blatt
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. C. F. Roos
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

P.H., B.P.L. and C.F.R. developed the research, based on theoretical ideas conceived with P.Z.; P.J., B.P.L., C. H. and C.F.R. performed the experiments; B.P.L., P.J., C.F.R. and P.H. analysed the data and carried out numerical simulations. P.J., C.H., B.P.L., R.B. and C.F.R. contributed to the experiment; B.P.L., C.F.R., P.H., P.Z. and R.B. wrote the manuscript; all authors contributed to discussions of the results and of the manuscript.

Corresponding author

Correspondence to C. F. Roos.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Extended data figures and tables

Extended Data Figure 1 Quantum dynamics following local quenches in a seven-ion (seven-spin) system.

a–c, Time evolution of the spatially resolved magnetization (colour coded as in Fig. 2) for three different local quenches. In each panel measured data (left-hand side) is shown next to theoretical calculations for the ideal case (right-hand side). a and d, Quench at the centre spin, α ≈ 1.36; b and e, quench at the leftmost spin, α ≈ 1.36; c and f, quench at both ends of the chain, α ≈ 1.75. Theoretical calculations employ measured laser–ion coupling strengths and distribution across the ion chain.

Extended Data Figure 2 Quantum dynamics following a global quench in a seven-ion (seven-spin) system.

a, Measured correlation matrices with elements (colour coded) at t = 0 ms, 5 ms, and 10 ms (α ≈ 1.75). b, Measured average magnetic spin–spin correlations (colour coded) as a function of time and distance n where the average was taken over all spin pairs (i, j) with |i − j| = n. c, Calculated spin–spin correlations (colour code: note the different colour scale) as a function of time and distance.

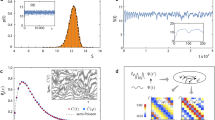
Extended Data Figure 3 Entanglement distributed by quasiparticles.

Following a quench of the central spin with short-range interactions (α ≈ 1.75), a distinct wavefront emerges. Each panel shows data (left-hand side) and theory (right-hand side) a, Measured single-spin magnetization (colour coded as in Fig. 2). b, Single-spin von Neumann entropy −Tr(ρlog(ρ)) normalized to one, derived from measured density matrices. Zero would correspond to a fully pure quantum state (black) and one (white) to a fully mixed state. The increase in entropy of any individual spin during the dynamics reflects the generation of entanglement with other spins. c, Real part of the tomographically reconstructed full density matrix of spins 3 and 5 at a time 9 ms after the quench. Imaginary parts are less than 0.03. The fidelity between the full experimentally reconstructed ρ and ideal state |ψ〉 is F = 0.975 ± 0.005, using .

Extended Data Figure 4 Quantum dynamics following a local quench in a 15-ion (15-spin) system.

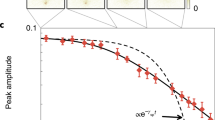
a–c, Experimentally measured time evolution of (as in Fig. 4a–c). d–f, Theoretical calculations based on a measured spin–spin interaction matrix (such as presented in Fig. 1b). h–i, Theoretical calculations using , with and α extracted from a fit to the measured dispersion relation. All theory calculations are done in the single-excitation subspace. j–l, Magnetization of symmetric pairs around the centre ion as a function of time: blue, ions 7 and 9; cyan, ions 6 and 10; purple, ions 5 and 11); red, ions 4 and 12; black, ions 3 and 13. The dashed lines are Gaussian fits to the measured arrival time of the first quasiparticle maximum (from a–c). m–o, Excluding the outermost ion to reduce finite-size effects, the fitted measured arrival maxima (circles) trace approximately a straight line when plotted against distance from quench site. A linear fit (solid line) yields an estimate for the propagation speed of the first quasiparticle maximum.

Extended Data Figure 5 Example of a spin–spin interaction matrix Jij.

The plot compares theory and experiment. Each element of the Jij matrix is measured directly (see Methods) in a system of N = 7 spins (solid coloured bars). Overlaid transparent bars with blue edges correspond to the results of a simulation which takes the following experimental parameters into account: the trapping frequencies; frequency of the bichromatic laser beams (see Methods); and measured individual laser–ion Rabi frequencies. The experimental data shown here are the same as in Fig. 1c. The elements J16, J27 and J17 were not measured. Small black vertical lines show one standard deviation in the experimentally measured elements.

PowerPoint slides

Rights and permissions

Reprints and Permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Jurcevic, P., Lanyon, B., Hauke, P. et al. Quasiparticle engineering and entanglement propagation in a quantum many-body system. Nature 511, 202–205 (2014). https://doi.org/10.1038/nature13461

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature13461

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing