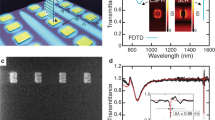
Abstract
Intersubband transitions in n-doped multi-quantum-well semiconductor heterostructures make it possible to engineer one of the largest known nonlinear optical responses in condensed matter systems—but this nonlinear response is limited to light with electric field polarized normal to the semiconductor layers1,2,3,4,5,6,7. In a different context, plasmonic metasurfaces (thin conductor–dielectric composite materials) have been proposed as a way of strongly enhancing light–matter interaction and realizing ultrathin planarized devices with exotic wave properties8,9,10,11. Here we propose and experimentally realize metasurfaces with a record-high nonlinear response based on the coupling of electromagnetic modes in plasmonic metasurfaces with quantum-engineered electronic intersubband transitions in semiconductor heterostructures. We show that it is possible to engineer almost any element of the nonlinear susceptibility tensor of these structures, and we experimentally verify this concept by realizing a 400-nm-thick metasurface with nonlinear susceptibility of greater than 5 × 104 picometres per volt for second harmonic generation at a wavelength of about 8 micrometres under normal incidence. This susceptibility is many orders of magnitude larger than any second-order nonlinear response in optical metasurfaces measured so far12,13,14,15. The proposed structures can act as ultrathin highly nonlinear optical elements that enable efficient frequency mixing with relaxed phase-matching conditions, ideal for realizing broadband frequency up- and down-conversions, phase conjugation and all-optical control and tunability over a surface.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Fejer, M. M. et al. Observation of extremely large quadratic susceptibility at 9.6–10.8 μm in electric-field-biased AlGaAs quantum wells. Phys. Rev. Lett. 62, 1041–1044 (1989)
Rosencher, E., Bois, P., Nagle, J. & Delaitre, S. Second harmonic generation by intersubband transitions in compositionally asymmetrical MQWs. Electron. Lett. 25, 1063–1065 (1989)
Capasso, F., Sirtori, C. & Cho, A. Y. Coupled-quantum-well semiconductors with giant electric-field tunable nonlinear-optical properties in the infrared. IEEE J. Quantum Electron. 30, 1313–1326 (1994)
Rosencher, E. et al. Quantum engineering of optical nonlinearities. Science 271, 168–173 (1996)
Gmachl, C. et al. Optimized second-harmonic generation in quantum cascade lasers. IEEE J. Quantum Electron. 39, 1345–1355 (2003)
Belkin, M. A. et al. Terahertz quantum-cascade-laser source based on intracavity difference-frequency generation. Nature Photon. 1, 288–292 (2007)
Vijayraghavan, K. et al. Broadly tunable terahertz generation in mid-infrared quantum cascade lasers. Nature Commun. 4, 2021 (2013)
Liu, X. L. et al. Taming the blackbody with infrared metamaterials as selective thermal emitters. Phys. Rev. Lett. 107, 045901 (2011)
Yu, N. F. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science 334, 333–337 (2011)
Ni, X. J. et al. Broadband light bending with plasmonic nanoantennas. Science 335, 427 (2012)
Monticone, F., Estakhri, N. M. & Alu, A. Full control of nanoscale optical transmission with a composite metascreen. Phys. Rev. Lett. 110, 203903 (2013)
Klein, M. W., Enkrich, C., Wegener, M. & Linden, S. Second-harmonic generation from magnetic metamaterials. Science 313, 502–504 (2006)
Feth, N. et al. Second-harmonic generation from complementary split-ring resonators. Opt. Lett. 33, 1975–1977 (2008)
Fan, W. J. et al. Second harmonic generation from patterned GaAs inside a subwavelength metallic hole array. Opt. Express 14, 9570–9575 (2006)
Niesler, F. B. P. et al. Second-harmonic generation from split-ring resonators on a GaAs substrate. Opt. Lett. 34, 1997–1999 (2009)
Pendry, J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000)
Fang, N., Lee, H., Sun, C. & Zhang, X. Sub-diffraction-limited optical imaging with a silver superlens. Science 308, 534–537 (2005)
Leonhardt, U. Optical conformal mapping. Science 312, 1777–1780 (2006)
Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006)
Chen, P. Y., Soric, J. & Alu, A. Invisibility and cloaking based on scattering cancellation. Adv. Mater. 24, Op281–Op304 (2012)
Pendry, J. B. Time reversal and negative refraction. Science 322, 71–73 (2008)
Rose, A. & Smith, D. R. Overcoming phase mismatch in nonlinear metamaterials. Opt. Mater. Express 1, 1232–1243 (2011)
Argyropoulos, C. et al. Nonlinear plasmonic cloaks to realize giant all-optical scattering switching. Phys. Rev. Lett. 108, 263905 (2012)
Hugi, A. et al. Mid-infrared frequency comb based on a quantum cascade laser. Nature 492, 229–233 (2012)
Vodopyanov, K. L. et al. Phase-matched second harmonic generation in asymmetric double quantum wells. Appl. Phys. Lett. 72, 2654–2656 (1998)
Vurgaftman, I., Meyer, J. R. & RamMohan, L. R. Optimized second-harmonic generation in asymmetric double quantum wells. IEEE J. Quantum Electron. 32, 1334–1346 (1996)
Boyd, R. W. Nonlinear Optics (Academic, 2008)
Todorov, Y. et al. Ultrastrong light-matter coupling regime with polariton dots. Phys. Rev. Lett. 105, 196402 (2010)
Benz, A. et al. Strong coupling in the sub-wavelength limit using metamaterial nanocavities. Nature Commun. 4, 2882 (2013)
Ellenbogen, T., Seo, K. & Crozier, K. B. Chromatic plasmonic polarizers for active visible color filtering and polarimetry. Nano Lett. 12, 1026–1031 (2012)
Zhao, Y. & Alu, A. Tailoring the dispersion of plasmonic nanorods to realize broadband optical meta-waveplates. Nano Lett. 13, 1086–1091 (2013)
Balanis, C. A. Advanced Engineering Electromagnetics (Wiley, 1989)
Vodopyanov, K. L. et al. Intersubband absorption saturation study of narrow III–V multiple quantum wells in the λ = 2.8–9 μm spectral range. Semicond. Sci. Technol. 12, 708–714 (1997)
Acknowledgements
This work was supported by NSF EAGER grant no. 1348049 (to M.A.B. and A.A.), AFOSR YIP award no. FA9550-10-1-0076 (M.A.B.), AFOSR YIP award no. FA9550-11-1-0009 (A.A.), and ONR MURI grant no. N00014-10-1-0942 (A.A.). The Walter Schottky Institute group acknowledges support from the Excellence Cluster ‘Nano Initiative Munich (NIM)’. Sample fabrication was carried out in the Microelectronics Research Center at the University of Texas at Austin, which is a member of the National Nanotechnology Infrastructure Network.
Author information
Authors and Affiliations
Contributions
J.L. designed the semiconductor heterostructure, calculated physical parameters and performed all fabrication and experimental measurements; M.T., C.A. and P.-Y.C. performed theoretical computations and structure optimization; F.L. assisted in experimental measurements; F.D., G.B. and M.-C.A. performed the semiconductor heterostructure growth; M.A.B. conceived the concept and the experiment; M.A.B. and A.A. developed the concept and planned and directed the research; and J.L., M.T., C.A., A.A. and M.A.B. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
Extended Data Figure 1 Intersubband absorption measurement.
Intersubband absorption spectrum of the wafer used in our experiments after background correction. Bottom y axis, wavenumber ( = 1/λ); top y axis, energy ( = hν). Inset, measurement geometry.
Extended Data Figure 2 Structures with plasmonic resonances detuned from intersubband transition frequencies.
a, Linear absorption spectrum of a metasurface in which plasmonic resonances were not well-overlapped spectrally with intersubband transitions of the MQW structure for fundamental and SH frequencies. b, SH peak power (left axis) or intensity (right axis) as a function of FF peak power squared (bottom axis) or peak intensity squared (top axis) for different input/output polarization combinations (yyy and so on, see key) at FF pump wavenumber 1/λpump = 1,310 cm−1 and SH wavenumber 2,620 cm−1 both in resonance with the plasmonic absorption peaks. SH response was close to the noise limit of our setup. Inset, SEM image of the metasurface. c, SH peak power output as a function of FF peak power squared (bottom axis) or peak intensity squared (top axis) for different input/output polarization combinations at FF wavenumber 1,240 cm−1 and SHG wavenumber of 2,480 cm−1, both away from plasmonic resonances of the metasurface but in resonance with intersubband transitions in the MQW structure.
Extended Data Figure 3 Nonlinear response saturation mechanism.
a, SH peak power output as a function of FF peak power squared (bottom axis) or peak intensity squared (top axis) at FF wavenumber 1,240 cm−1. Black curve, data for the pump laser operating with 400 ns pulses (same as used in the main text); red curve, data for the pump laser operating with 60 ns pulses. A slight difference in the SHG power for 60 ns and 400 ns FF input is attributed to slight changes in the pulse shape and detector response for 400 ns and 60 ns pulses. b, SH conversion efficiency versus FF peak power (bottom axis) or peak intensity (top axis) for FF wavenumber 1,240 cm−1 (red) and 1,280 cm−1 (blue). Straight lines show expected linear dependence of SH conversion efficiency on FF power for the cases in the absence of intensity saturation.
Extended Data Figure 4 SHG at oblique incidence.
a, Optical set-up for metasurface characterization at 45° incidence angle. LP and SP are long- and short-pulse filters, respectively. HWP is a half-wave plate for FF polarization control. Directions of S- and P-polarizations and orientation of the metasurface are indicated. Inset, SEM image of the metasurface with x and y axes shown. b, Measured SH peak power output as a function of FF peak power squared (bottom axis) or peak intensity squared (top axis) at FF wavenumber 1,240 cm−1 for different input/output polarization combinations (SSS and so on, see key). c, Simulated absorption spectrum of the metasurface at 45° incidence for different input light polarizations.
Rights and permissions
About this article
Cite this article
Lee, J., Tymchenko, M., Argyropoulos, C. et al. Giant nonlinear response from plasmonic metasurfaces coupled to intersubband transitions. Nature 511, 65–69 (2014). https://doi.org/10.1038/nature13455
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13455
This article is cited by
-
Frequency-hopping wave engineering with metasurfaces
Nature Communications (2024)
-
Three-dimensional nonlinear optical materials from twisted two-dimensional van der Waals interfaces
Nature Photonics (2024)
-
Poincaré sphere trajectory encoding metasurfaces based on generalized Malus’ law
Nature Communications (2024)
-
Electronic transport driven by collective light-matter coupled states in a quantum device
Nature Communications (2023)
-
Integrated metasurfaces for re-envisioning a near-future disruptive optical platform
Light: Science & Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.