Abstract
Quantum error correction is required for a practical quantum computer because of the fragile nature of quantum information. In quantum error correction, information is redundantly stored in a large quantum state space and one or more observables must be monitored to reveal the occurrence of an error, without disturbing the information encoded in an unknown quantum state. Such observables, typically multi-quantum-bit parities, must correspond to a special symmetry property inherent in the encoding scheme. Measurements of these observables, or error syndromes, must also be performed in a quantum non-demolition way (projecting without further perturbing the state) and more quickly than errors occur. Previously, quantum non-demolition measurements of quantum jumps between states of well-defined energy have been performed in systems such as trapped ions1,2,3, electrons4, cavity quantum electrodynamics5,6, nitrogen–vacancy centres7,8,9 and superconducting quantum bits10,11. So far, however, no fast and repeated monitoring of an error syndrome has been achieved. Here we track the quantum jumps of a possible error syndrome, namely the photon number parity of a microwave cavity, by mapping this property onto an ancilla quantum bit, whose only role is to facilitate quantum state manipulation and measurement. This quantity is just the error syndrome required in a recently proposed scheme for a hardware-efficient protected quantum memory using Schrödinger cat states (quantum superpositions of different coherent states of light) in a harmonic oscillator12. We demonstrate the projective nature of this measurement onto a region of state space with well-defined parity by observing the collapse of a coherent state onto even or odd cat states. The measurement is fast compared with the cavity lifetime, has a high single-shot fidelity and has a 99.8 per cent probability per single measurement of leaving the parity unchanged. In combination with the deterministic encoding of quantum information in cat states realized earlier13,14, the quantum non-demolition parity tracking that we demonstrate represents an important step towards implementing an active system that extends the lifetime of a quantum bit.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Bergquist, J. C., Hulet, R. G., Itano, W. M. & Wineland, D. J. Observation of quantum jumps in a single atom. Phys. Rev. Lett. 57, 1699–1702 (1986)
Sauter, T., Neuhauser, W., Blatt, R. & Toschek, P. E. Observation of quantum jumps. Phys. Rev. Lett. 57, 1696–1698 (1986)
Nagourney, W., Sandberg, J. & Dehmelt, H. Shelved optical electron amplifier: observation of quantum jumps. Phys. Rev. Lett. 56, 2797–2799 (1986)
Peil, S. & Gabrielse, G. Observing the quantum limit of an electron cyclotron: QND measurements of quantum jumps between Fock states. Phys. Rev. Lett. 83, 1287–1290 (1999)
Gleyzes, S. et al. Quantum jumps of light recording the birth and death of a photon in a cavity. Nature 446, 297–300 (2007)
Guerlin, C. et al. Progressive field-state collapse and quantum non-demolition photon counting. Nature 448, 889–893 (2007)
Jelezko, F. et al. Single spin states in a defect center resolved by optical spectroscopy. Appl. Phys. Lett. 81, 2160–2162 (2002)
Neumann, P. et al. Single-shot readout of a single nuclear spin. Science 329, 542–544 (2010)
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011)
Vijay, R., Slichter, D. H. & Siddiqi, I. Observation of quantum jumps in a superconducting artificial atom. Phys. Rev. Lett. 106, 110502 (2011)
Hatridge, M. et al. Quantum back-action of an individual variable-strength measurement. Science 339, 178–181 (2013)
Leghtas, Z. et al. Hardware-efficient autonomous quantum error correction. Phys. Rev. Lett. 111, 120501 (2013)
Leghtas, Z. et al. Deterministic protocol for mapping a qubit to coherent state superposition in a cavity. Phys. Rev. A 87, 042315 (2013)
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 342, 607–610 (2013)
Deléglise, S. et al. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514 (2008)
Sayrin, C. et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 477, 73–77 (2011)
Devoret, M. H. & Schoelkopf, R. J. Superconducting circuits for quantum information: an outlook. Science 339, 1169–1174 (2013)
Castellanos-Beltran, M. A., Irwin, K. D., Hilton, G. C., Vale, L. R. & Lehnert, K. W. Amplification and squeezing of quantum noise with a tunable Josephson metamaterial. Nature Phys. 4, 929–931 (2008)
Bergeal, N. et al. Phase-preserving amplification near the quantum limit with a Josephson ring modulator. Nature 465, 64–68 (2010)
Ristè, D. et al. Deterministic entanglement of superconducting qubits by parity measurement and feedback. Nature 502, 350–354 (2013)
Haroche, S. & Raimond, J. M. Exploring the Quantum: Atoms, Cavities, and Photons (Oxford Univ. Press, 2006)
Paik, H. et al. Observation of high coherence in Josephson junction qubits measured in a three-dimensional circuit QED architecture. Phys. Rev. Lett. 107, 240501 (2011)
Kirchmair, G. et al. Observation of quantum state collapse and revival due to the single-photon Kerr effect. Nature 495, 205–209 (2013)
Kamal, A., Marblestone, A. & Devoret, M. H. Signal-to-pump back action and self-oscillation in double-pump Josephson parametric amplifier. Phys. Rev. B 79, 184301 (2009)
Murch, K. W., Weber, S. J., Macklin, C. & Siddiqi, I. Observing single quantum trajectories of a superconducting quantum bit. Nature 502, 211–214 (2013)
Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007)
Bertet, P. et al. Direct measurement of the Wigner function of a one-photon Fock state in a cavity. Phys. Rev. Lett. 89, 200402 (2002)
Brune, M., Haroche, S., Raimond, J. M., Davidovich, L. & Zagury, N. Manipulation of photons in a cavity by dispersive atom-field coupling: Quantum-nondemolition measurements and generation of “Schrödinger” cat states. Phys. Rev. A 45, 5193–5214 (1992)
Brune, M. et al. Observing the progressive decoherence of the “meter” in a quantum measurement. Phys. Rev. Lett. 77, 4887–4890 (1996)
Reagor, M. et al. Ten milliseconds for aluminum cavities in the quantum regime. Appl. Phys. Lett. 102, 192604 (2013)
Siddiqi, I. et al. Direct observation of dynamical bifurcation between two driven oscillation states of a Josephson junction. Phys. Rev. Lett. 94, 027005 (2005)
Vijay, R., Devoret, M. H. & Siddiqi, I. The Josephson bifurcation amplifier. Rev. Sci. Instrum. 80, 111101 (2009)
Belavkin, V. P. Quantum stochastic calculus and quantum nonlinear filtering. J. Multivariate Anal. 42, 171–201 (1992)
Bouten, L., van Handel, R. & James, M. An introduction to quantum filtering. SIAM J. Contr. Optim. 46, 2199–2241 (2007)
Mirrahimi, M. et al. Dynamically protected cat-qubits: a new paradigm for universal quantum computation. New J. Phys. 16, 045014 (2014)
Acknowledgements
We thank L. Jiang and S. M. Girvin for discussions. Facilities use was supported by the Yale Institute for Nanoscience and Quantum Engineering and the US NSF MRSEC DMR 1119826. This research was supported in part by the Office of the Director of National Intelligence (ODNI), Intelligence Advanced Research Projects Activity (IARPA), through the Army Research Office (W911NF-09-1-0369) and in part by the US Army Research Office (W911NF-09-1-0514). All statements of fact, opinion or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of IARPA, the ODNI or the US government. M.M. acknowledges partial support from the Agence National de Recherche under the project EPOQ2, ANR-09-JCJC-0070. B.V. acknowledges partial support from NSF under the project PHY-1309996.
Author information
Authors and Affiliations
Contributions
L.S. and A.P. performed the experiment and analysed the data. Z.L. and M.M. provided theoretical support. B.V. and G.K. provided further experimental contributions. K.M.S., A.N., M.H. and S.S. contributed to the double-pumped Josephson bifurcation amplifier under the supervision of M.H.D. J.B. and L.F. fabricated the device. R.J.S. designed and supervised the project. L.S., A.P., L.F. and R.J.S. wrote the manuscript with feedback from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Extended data figures and tables
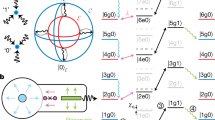
Extended Data Figure 1 Schematic of the measurement set-up.
We use two separate lines to drive the readout and the storage cavity. Qubit state manipulations are realized through the readout cavity input line. The readout cavity output signal is first amplified by a JBA operating in a double-pumped mode, and the reflected signal then goes through three isolators in series before being further amplified by a HEMT at 4 K. The amplified signal is finally down-converted to 50 MHz and then digitized by a fast 1 GS data-acquisition card.
Extended Data Figure 2 Poisson distribution of photon numbers in the cavity.
Dotted colour lines are data for the first eight Fock states n = 0, 1, 2, …, 7 as functions of displacement amplitude |α|. The measurements are performed with a selective π-pulse on each number splitting peak, and the resulting signal amplitude should be proportional to the corresponding number population. These oscillation amplitudes have been normalized to probabilities such that the sum of the amplitudes corresponding to n = 0 and n = 1 equals unity. Dashed lines are theoretical curves with a Poisson distribution  , where the x axis has had a single scale factor adjusted to fit all these probabilities. The excellent agreement indicates good control of the coherent state in the cavity and also gives a good calibration of the cavity displacement amplitude. On the basis of the probability of n = 1 at |α| = 0, we find a background photon population of nth = 0.02 in the cavity. Inset bottom panel: spectroscopy (left axis) of the number splitting peaks of the qubit when populating different photon numbers in the cavity. Inset top panel: difference between peak positions and a linear fit. The curvature necessitates a second-order polynomial fit, resulting in a linear dispersive shift χqs/2π = 1.789 ± 0.002 MHz and a nonlinear dispersive shift
, where the x axis has had a single scale factor adjusted to fit all these probabilities. The excellent agreement indicates good control of the coherent state in the cavity and also gives a good calibration of the cavity displacement amplitude. On the basis of the probability of n = 1 at |α| = 0, we find a background photon population of nth = 0.02 in the cavity. Inset bottom panel: spectroscopy (left axis) of the number splitting peaks of the qubit when populating different photon numbers in the cavity. Inset top panel: difference between peak positions and a linear fit. The curvature necessitates a second-order polynomial fit, resulting in a linear dispersive shift χqs/2π = 1.789 ± 0.002 MHz and a nonlinear dispersive shift  .
.
Extended Data Figure 3 Ensemble-averaged free parity evolution of a coherent state.
The measurement protocol is shown in the inset. The single parity measurement gives a readout voltage that has been converted to parity through thresholding. All measured evolution curves saturate at the same value in the long time limit. This saturation level has been forced to 0.96 (because nth = 0.02), represented by the dashed horizontal line. The solid lines are global fits, giving a time constant of τ0 = 55 µs.
Extended Data Figure 4 Effectiveness of the  pulse.
pulse.
Blue and red data (bottom axis) are ensemble-averaged qubit readouts after consecutively (with no wait time) applying ( ,
,  ) and (
) and ( ,
,  ), respectively, as functions of different
), respectively, as functions of different  introduced into the cavity. The curvature for
introduced into the cavity. The curvature for  comes from the finite bandwidth of the pulses in the frequency domain. Green curve (top axis) is a time Rabi trace for an amplitude comparison with no initial cavity displacement.
comes from the finite bandwidth of the pulses in the frequency domain. Green curve (top axis) is a time Rabi trace for an amplitude comparison with no initial cavity displacement.
Extended Data Figure 5 Qubit readout properties.
a, Histogram of qubit readout for the parity protocol used in repeated single-shot traces in Fig. 3. The phase between the JBA readout and the pump has been adjusted such that |g〉, |e〉 and |f〉 states can be distinguished with optimal spacings. Thresholds between |g〉 and |e〉, and between |e〉 and |f〉, have been chosen to digitize the readout signal to +1, −1 and 0 for |g〉, |e〉 and |f〉, respectively. Note that we assign a zero to the |f〉 states to indicate a ‘failed’ measurement with no useful information about the parity. b–d, Illustrations of pulse sequences (not to scale) producing the readout error matrix with the storage cavity left in vacuum. The |g〉 state (b) is prepared through post-selection of an initial qubit measurement M1, whereas |e〉 (c) and |f〉 (d) are prepared by properly pulsing the selected |g〉 state. A histogram of the second measurement, M2, gives the qubit readout properties. e, Qubit readout properties for qubit initially in |g〉, |e〉 and |f〉, respectively.
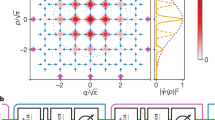
Extended Data Figure 6 Parity readout properties and Wigner tomography.
a, Parity readout property for given even and odd parity states for the protocol ( as the second qubit pulse) used in the single-shot traces in Fig. 3 (
as the second qubit pulse) used in the single-shot traces in Fig. 3 ( ). b, Protocol to measure parity readout fidelity. An initial qubit measurement allows a post-selection of the |g〉 state of the qubit, followed by six consecutive parity measurements. The pulse sequence of each parity measurement is shown in P1 in c.
). b, Protocol to measure parity readout fidelity. An initial qubit measurement allows a post-selection of the |g〉 state of the qubit, followed by six consecutive parity measurements. The pulse sequence of each parity measurement is shown in P1 in c.  are determined by post-selecting the cases with the first five consecutive identical parity results, which give the photon state parity with good confidence, and then constructing a histogram for the sixth parity measurement. c, Illustration of pulse sequence (not to scale) for producing the cat states and the Wigner tomography shown in Fig. 2. The protocol starts with a post-selection of the |g〉 state of the qubit through an initial qubit measurement M1. A parity measurement is performed immediately after a storage cavity displacement α, followed by Wigner tomography with varying displacements β. A 280 ns waiting time after each measurement has been chosen to ensure that the readout cavity is in the vacuum state. The qubit pulses have a Gaussian envelope truncated to 4σ = 8 ns, and the displacement pulses on the storage cavity are 10 ns square pulses. The dashed enclosures represent the pulse sequences for parity measurement. d, Error budgets for Wigner tomography fidelity. e, Error budgets for the parity readout fidelities with
are determined by post-selecting the cases with the first five consecutive identical parity results, which give the photon state parity with good confidence, and then constructing a histogram for the sixth parity measurement. c, Illustration of pulse sequence (not to scale) for producing the cat states and the Wigner tomography shown in Fig. 2. The protocol starts with a post-selection of the |g〉 state of the qubit through an initial qubit measurement M1. A parity measurement is performed immediately after a storage cavity displacement α, followed by Wigner tomography with varying displacements β. A 280 ns waiting time after each measurement has been chosen to ensure that the readout cavity is in the vacuum state. The qubit pulses have a Gaussian envelope truncated to 4σ = 8 ns, and the displacement pulses on the storage cavity are 10 ns square pulses. The dashed enclosures represent the pulse sequences for parity measurement. d, Error budgets for Wigner tomography fidelity. e, Error budgets for the parity readout fidelities with  as the second qubit pulse.
as the second qubit pulse.
Extended Data Figure 7 Schematic of the quantum filter.
At time t, the density matrix of the photon state is ρ(Ct), which depends on all previous correlations. At t + dt, only considering the decoherence of the cavity, the expected density matrix from free evolution becomes  . The additional information Ct+dt acquired from the parity measurement at t + dt changes the knowledge of the parity of the photon state according to equation (1).
. The additional information Ct+dt acquired from the parity measurement at t + dt changes the knowledge of the parity of the photon state according to equation (1).
Extended Data Figure 8 Effectiveness and response time of the quantum filter.
a, Ensemble-averaged parity dynamics obtained directly from the correlation of qubit states between neighbouring parity measurements. The data set is the same as that shown in Fig. 4. Solid lines are predictions based on equation (2), in excellent agreement with the measured data. The offset of the averaged parity at t = 0 comes from the asymmetry between the parity readout fidelities of the even and odd states. The fact that the saturated parity value in the long time limit is much lower than that in Fig. 4 is additional proof of the effectiveness of the quantum filter. b, Effectiveness of the quantum filter. Blue (raw) and red (filtered) curves are the same as those shown in Fig. 3e. The green curve is the direct correlation of qubit states between neighbouring parity measurements. The red curve is clearly much smoother and can reject the brief changes in the green curve. c, Response time of the quantum filter applied to typical photon jump events. The blue curve is the raw data from a repeated parity measurement. The red curve is the corresponding parity estimator based on the quantum filter. Green and cyan curves are fits to tanh functions of the parity estimator at the transitions down and up, respectively, giving a transition time constant of less than 1 µs. However, the response time of the filter to make a transition between −0.9 and +0.9 is τf ≈ 2 µs.
Extended Data Figure 9 Histograms of the number of jumps extracted from the parity estimator during 500 µs repeated parity measurements for an initial even or odd cat state by post-selection.
a, b, |α| = 2.0; c, d, |α| = 1.4; e, f, |α| = 1.0. Solid lines are numerical simulations including the background thermal excitation and finite response time of the quantum filter. In the simulation, we use a coherent state as the initial state without distinguishing the parity. The good agreement between data and simulation demonstrates that the repeated parity measurement can track the error syndromes faithfully.
Rights and permissions
About this article
Cite this article
Sun, L., Petrenko, A., Leghtas, Z. et al. Tracking photon jumps with repeated quantum non-demolition parity measurements. Nature 511, 444–448 (2014). https://doi.org/10.1038/nature13436
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature13436
This article is cited by
-
Protecting entanglement between logical qubits via quantum error correction
Nature Physics (2024)
-
Generation of a hybrid W entangled state of three photonic qubits with different encodings
Quantum Information Processing (2024)
-
Preparation of maximally-entangled states with multiple cat-state qutrits in circuit QED
Frontiers of Physics (2024)
-
Shortcuts to adiabaticity in superconducting circuits for fast multi-partite state generation
Communications Physics (2023)
-
Autonomous quantum error correction in a four-photon Kerr parametric oscillator
npj Quantum Information (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.


 pulse.
pulse.