Abstract
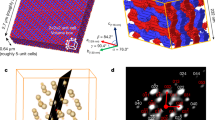
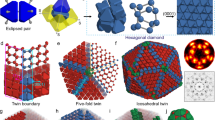
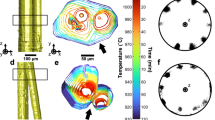
Over the past decade, quasicrystalline order1 has been observed in many soft-matter systems: in dendritic micelles2, in star3 and tetrablock4 terpolymer melts and in diblock copolymer5 and surfactant micelles6. The formation of quasicrystals7,8,9 from such a broad range of ‘soft’ macromolecular micelles suggests that they assemble by a generic mechanism rather than being dependent on the specific chemistry of each system. Indeed, micellar softness has been postulated7 and shown to lead to quasicrystalline order10. Here we theoretically explore this link by studying two-dimensional hard disks decorated with step-like square-shoulder repulsion that mimics, for example, the soft alkyl shell around the aromatic core in dendritic micelles2. We find a family of quasicrystals with 10-, 12-, 18- and 24-fold bond orientational order which originate from mosaics of equilateral and isosceles triangles formed by particles arranged core-to-core and shoulder-to-shoulder. The pair interaction responsible for these phases highlights the role of local packing geometry in generating quasicrystallinity in soft matter, complementing the principles that lead to quasicrystal formation in hard tetrahedra11,12. Based on simple interparticle potentials, quasicrystalline mosaics may well find use in diverse applications ranging from improved image reproduction13 to advanced photonic materials14.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Levine, D. & Steinhardt, P. J. Quasicrystals—a new class of ordered structures. Phys. Rev. Lett. 53, 2477–2480 (1984)
Zeng, X. et al. Supramolecular dendritic liquid quasicrystals. Nature 428, 157–160 (2004)
Hayashida, K., Dotera, T., Takano, A. & Matsushita, Y. Polymeric quasicrystal: mesoscopic quasicrystalline tiling in ABC star polymers. Phys. Rev. Lett. 98, 195502 (2007)
Zhang, J. & Bates, F. S. Dodecagonal quasicrystalline morphology in a poly(styrene-b-isoprene-b-styrene-b-ethylene oxide) tetrablock terpolymer. J. Am. Chem. Soc. 134, 7636–7639 (2012)
Fischer, S. et al. Colloidal quasicrystals with 12-fold and 18-fold diffraction symmetry. Proc. Natl Acad. Sci. USA 108, 1810–1814 (2011)
Xiao, C., Fujita, N., Miyasaka, K., Sakamoto, Y. & Terasaki, O. Dodecagonal tiling in mesoporous silica. Nature 487, 349–353 (2012)
Ungar, G. & Zeng, X. Frank-Kasper, quasicrystalline and related phases in liquid crystals. Soft Matter 1, 95–106 (2005)
Lifshitz, R. & Diamant, H. Soft quasicrystals—why are they stable? Phil. Mag. 87, 3021–3030 (2007)
Mikhael, J., Roth, J., Helden, L. & Bechinger, C. Archimedean-like tiling on decagonal quasicrystalline surfaces. Nature 454, 501–504 (2008)
Iacovella, C. R., Keys, A. S. & Glotzer, S. C. Self-assembly of soft-matter quasicrystals and their approximants. Proc. Natl Acad. Sci. USA 108, 20935–20940 (2011)
Haji-Akbari, A. et al. Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra. Nature 462, 773–777 (2009)
Damasceno, P. F., Engel, M. & Glotzer, S. C. Predictive self-assembly of polyhedra into complex structures. Science 337, 453–457 (2012)
Steinhardt, P. J. & Taylor, P. Methods and apparatus for eliminating moiré interference using quasiperiodic patterns. US Patent Number 4,894,726. (16 January 1989)
Zoorob, M. E., Charlton, M. D. B., Parker, G. J., Baumberg, J. J. & Netti, M. C. Complete photonic bandgaps in 12-fold symmetric quasicrystals. Nature 404, 740–743 (2000)
Grünbaum, B. & Shephard, G. C. Tilings and Patterns Ch. 10 (Freeman, 1986)
Barkan, K., Diamant, H. & Lifshitz, R. Stability of quasicrystals composed of soft isotropic particles. Phys. Rev. B 83, 172201 (2011)
Skibinsky, A., Buldyrev, S. V., Scala, A., Havlin, S. & Stanley, H. E. Quasicrystals in a monodisperse system. Phys. Rev. E 60, 2664–2669 (1999)
Jagla, E. A. Phase behavior of a system of particles with core collapse. Phys. Rev. E 58, 1478–1486 (1998)
Engel, M. & Trebin, H.-R. Self-assembly of monatomic complex crystals and quasicrystals with a double-well interaction potential. Phys. Rev. Lett. 98, 225505 (2007)
Lifshitz, R. & Petrich, D. M. Theoretical model for Faraday waves with multiple-frequency forcing. Phys. Rev. Lett. 79, 1261–1264 (1997)
Henley, C. L. Cell geometry for cluster-based quasicrystal model. Phys. Rev. B 43, 993–1020 (1991)
Alder, B. J. & Wainwright, T. E. Phase transition for a hard-sphere system. J. Chem. Phys. 27, 1208–1209 (1957)
Young, D. A. & Alder, B. J. Melting curve extrema from a repulsive “step” potential. Phys. Rev. Lett. 38, 1213–1216 (1977)
Malescio, G. & Pellicane, G. Stripe phases from isotropic repulsive interactions. Nature Mater. 2, 97–100 (2003)
Phillips, C. L. & Voth, G. A. Discovering crystals using shape matching and machine learning. Soft Matter 9, 8552–8568 (2013)
Oxborrow, M. & Henley, C. L. Random square-triangle tilings: a model for twelvefold-symmetric quasicrystals. Phys. Rev. B 48, 6966–6998 (1993)
Kawamura, H. Entropy of the random triangle-square tiling. Physica A 177, 73–78 (1991)
Lançon, F., Billard, L. & Chaudhari, P. Thermodynamical properties of a two-dimensional quasi-crystal from molecular dynamics calculations. Europhys. Lett. 2, 625–629 (1986)
Polik, W. F. & Burchard, W. Static light scattering from aqueous poly(ethylene oxide) solutions in the temperature range 20–90°C. Macromolecules 16, 978–982 (1983)
Motornov, M., Roiter, Y., Tokarev, I. & Minko, S. Stimuli-responsive nanoparticles, nanogels and capsules for integrated multifunctional intelligent systems. Prog. Polym. Sci. 35, 174–211 (2010)
Acknowledgements
We thank J. Dolinšek, M. Engel, S. Förster, N. Fujita, M. A. Glaser, C. L. Henley, G. Kahl, R. D. Kamien, Y. Kimura, R. Lifshitz, C. N. Likos, T. C. Lubensky, Y. Sakamoto, M. Schmiedeberg, A. Šiber and A. Takano for discussions. This work was supported by the Japan Society for the Promotion of Science through Grant-in-Aid for Scientific Research (C) (grant number 22540375), by the Slovenian Research Agency (grant number P1-0055) and by the Marie-Curie Initial Training Network COMPLOIDS under FP7-PEOPLE-ITN-2008 (grant number 234810).
Author information
Authors and Affiliations
Contributions
T.D. and P.Z. conceived the project, T.D. and T.O. performed simulations, and P.Z. proposed the tiling theory. T.D. and P.Z. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains a Supplementary Discussion, comprising Supplementary Text and Data 1-3, Supplementary Tables 1-3, Supplementary Figures 1-36 and additional references. (PDF 6343 kb)
Hexagonal-dodecagonal-decaoctatic transition
This video shows a 31-frame sequence of snapshots and diffraction patterns illustrating the transition from hexagonal crystal to HD12 dodecagonal phase and then to HD18 decaoctatic phase in hard-core/square-shoulder disks induced by cooling accompanied by a moderate 10% decrease of shoulder width. (MOV 11655 kb)
Rights and permissions
About this article
Cite this article
Dotera, T., Oshiro, T. & Ziherl, P. Mosaic two-lengthscale quasicrystals. Nature 506, 208–211 (2014). https://doi.org/10.1038/nature12938
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12938
This article is cited by
-
Quasi-crystalline order in vibrating granular matter
Nature Physics (2024)
-
Structural studies of local environments in high-symmetry quasicrystals
Scientific Reports (2023)
-
A columnar liquid quasicrystal with a honeycomb structure that consists of triangular, square and trapezoidal cells
Nature Chemistry (2023)
-
A regime beyond the Hall–Petch and inverse-Hall–Petch regimes in ultrafine-grained solids
Communications Physics (2022)
-
How to design an icosahedral quasicrystal through directional bonding
Nature (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.