Abstract
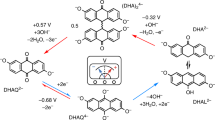
As the fraction of electricity generation from intermittent renewable sources—such as solar or wind—grows, the ability to store large amounts of electrical energy is of increasing importance. Solid-electrode batteries maintain discharge at peak power for far too short a time to fully regulate wind or solar power output1,2. In contrast, flow batteries can independently scale the power (electrode area) and energy (arbitrarily large storage volume) components of the system by maintaining all of the electro-active species in fluid form3,4,5. Wide-scale utilization of flow batteries is, however, limited by the abundance and cost of these materials, particularly those using redox-active metals and precious-metal electrocatalysts6,7. Here we describe a class of energy storage materials that exploits the favourable chemical and electrochemical properties of a family of molecules known as quinones. The example we demonstrate is a metal-free flow battery based on the redox chemistry of 9,10-anthraquinone-2,7-disulphonic acid (AQDS). AQDS undergoes extremely rapid and reversible two-electron two-proton reduction on a glassy carbon electrode in sulphuric acid. An aqueous flow battery with inexpensive carbon electrodes, combining the quinone/hydroquinone couple with the Br2/Br− redox couple, yields a peak galvanic power density exceeding 0.6 W cm−2 at 1.3 A cm−2. Cycling of this quinone–bromide flow battery showed >99 per cent storage capacity retention per cycle. The organic anthraquinone species can be synthesized from inexpensive commodity chemicals8. This organic approach permits tuning of important properties such as the reduction potential and solubility by adding functional groups: for example, we demonstrate that the addition of two hydroxy groups to AQDS increases the open circuit potential of the cell by 11% and we describe a pathway for further increases in cell voltage. The use of π-aromatic redox-active organic molecules instead of redox-active metals represents a new and promising direction for realizing massive electrical energy storage at greatly reduced cost.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others

References
Rugolo, J. & Aziz, M. J. Electricity storage for intermittent renewable sources. Energy Environ. Sci. 5, 7151–7160 (2012)
Yang, Z. et al. Electrochemical energy storage for green grid. Chem. Rev. 111, 3577–3613 (2011)
Weber, A. Z. et al. Redox flow batteries: a review. J. Appl. Electrochem. 41, 1137–1164 (2011)
Leung, P. et al. Progress in redox flow batteries, remaining challenges and their applications in energy storage. RSC Adv. 2, 10125–10156 (2012)
Nguyen, T. & Savinell, R. F. Flow batteries. Electrochem. Soc. Interface 19, 54–56 (2010)
Skyllas-Kazacos, M., Chakrabarti, M. H., Hajimolana, S. A., Mjalli, F. S. & Saleem, M. Progress in flow battery research and development. J. Electrochem. Soc. 158, R55–R79 (2011)
Huskinson, B., Rugolo, J., Mondal, S. K. & Aziz, M. J. A high power density, high efficiency hydrogen–chlorine regenerative fuel cell with a low precious metal content catalyst. Energy Environ. Sci. 5, 8690–8698 (2012)
Crossley, M. L. The separation of mono-β, 2,6- and 2,7-sulfonic acids of anthraquinone. J. Am. Chem. Soc. 37, 2178–2181 (1915)
Conant, J. B., Kahn, H. M., Fieser, L. F. & Kurtz, S. S. An electrochemical study of the reversible reduction of organic compounds. J. Am. Chem. Soc. 44, 1382–1396 (1922)
Kelsall, G. H. & Thompson, I. Redox chemistry of H2S oxidation by the British Gas Stretford process. Part III: Electrochemical behaviour of anthraquinone 2,7 disulphonate in alkaline electrolytes. J. Appl. Electrochem. 23, 296–307 (1993)
Forster, R. J. & O’Kelly, J. P. Protonation reactions of anthraquinone-2,7-disulphonic acid in solution and within monolayers. J. Electroanal. Chem. 498, 127–135 (2001)
Song, Y. & Buettner, G. R. Thermodynamic and kinetic considerations for the reaction of semiquinone radicals to form superoxide and hydrogen peroxide. Free Radic. Biol. Med. 49, 919–962 (2010)
Xu, Y. et al. in World Non-Grid-Connected Wind Power and Energy Conference 1–4 (IEEE, 2009)
Wang, W. et al. Anthraquinone with tailored structure for a nonaqueous metal-organic redox flow battery. Chem. Commun. 48, 6669–6671 (2012)
Yao, M. et al. High capacity organic positive-electrode material based on a benzoquinone derivative for use in rechargeable lithium batteries. J. Power Sources 195, 8336–8340 (2010)
Gordon, O. W., Plattner, E. & Doppenberg, F. Production of pulp by the soda-anthraquinone process (SAP) with recovery of the cooking chemicals. US patent 5,595,628. (1997)
US Geological Survey 2010 Minerals Yearbook: Bromine (2010); available at http://minerals.usgs.gov/minerals/pubs/commodity/bromine/myb1-2010-bromi.pdf
US Geological Survey Vanadium Mineral Commodities Summary (2013); available at http://minerals.usgs.gov/minerals/pubs/commodity/vanadium/mcs-2013-vanad.pdf
Skyllas-Kazacos, M., Milne, N. A. & Kazacos, G. C. Membrane properties and behavior in the Generation 2 vanadium bromide redox flow batteries. Materials Forum 32, 72–77 (2008)
Yeo, R. S. & McBreen, J. Transport properties of Nafion membranes in electrochemically regenerative hydrogen/halogen cells. J. Electrochem. Soc. 126, 1682–1687 (1979)
Haase, J., Baudys, J., Obruba, K. & Panek, J. Dihydroxyanthraquinone disulfonic acids. Czechoslovakian patent. 148,977 (1973)
Dewar, M. J. S. & Trinajstic, N. Ground states of conjugated molecules-XIV: redox potentials of quinones. Tetrahedron 25, 4529–4534 (1969)
Pullman, B. & Pullman, A. Quantum Biochemistry 475 (Interscience, 1963)
Guin, P. S., Das, S. & Mandal, P. C. Electrochemical reduction of quinones in different media: a review. Int. J. Electrochem. 816202 (2011).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996)
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994)
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999)
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993)
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996)
Qu, R., Liu, H., Feng, M., Yang, X. & Wang, Z. Investigation on intramolecular hydrogen bond and some thermodynamic properties of polyhydroxylated anthraquinones. J. Chem. Eng. Data 57, 2442–2455 (2012)
Mayo, S. L., Olafson, B. D. & Goddard, W. A., III Dreiding: a generic force field for molecular simulations. J. Phys. Chem. 94, 8897–8909 (1990)
Wang, J. & Hou, T. Recent advances on aqueous solubility prediction. Comb. Chem. High Throughput Screen. 14, 328–338 (2011)
Johnsson Wass, J. R. T., Ahlberg, E., Panas, I. & Schiffrin, D. J. Quantum chemical modeling of the reduction of quinones. J. Phys. Chem. A 110, 2005–2020 (2006)
Tannor, D. J. et al. Accurate first principles calculation of molecular charge distributions and solvation energies from ab initio quantum mechanics and continuum dielectric theory. J. Am. Chem. Soc. 116, 11875–11882 (1994)
Marten, B. et al. New model for calculation of solvation free energies: correction of self-consistent reaction field continuum dielectric theory for short-range hydrogen-bonding effects. J. Phys. Chem. 100, 11775–11788 (1996)
Hongo, K., Watson, M. A., Sánchez-Carrera, R. S., Iitaka, T. & Aspuru-Guzik, A. Failure of conventional density functionals for the prediction of molecular crystal polymorphism: a quantum Monte Carlo study. J. Phys. Chem. Lett. 1, 1789–1794 (2010)
Acknowledgements
This work was partially funded through US Department of Energy ARPA-E Award DE-AR0000348 and partially funded through the Harvard School of Engineering and Applied Sciences. Theoretical work was funded in part through the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number OCI-1053575. B.H. was supported by an NSF Graduate Research Fellowship. S.E. performed work as part of the Fellowships for Young Energy Scientists programme of the Foundation for Fundamental Research on Matter (FOM), which is part of the Netherlands Organization for Scientific Research (NWO). We thank T. Betley, L. Hartle, R. Burton and R. Duncan for discussions.
Author information
Authors and Affiliations
Contributions
B.H. and M.P.M. contributed equally to this work. B.H. and M.P.M. designed and tested the battery, with direction from M.J.A. Both M.P.M. and M.R.G. conducted electrochemistry experiments, with direction from M.J.A. M.P.M. and C.J.G. synthesized chemicals with direction from R.G.G. Theoretical calculations were done by C.S. and S.E., with input from M.P.M. and R.G.G. and direction from A.A.-G. X.C. contributed NMR results. B.H., M.P.M., C.S., M.R.G., S.E., A.A.G., R.G.G. and M.J.A. all contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
Harvard University has filed a patent on some of the intellectual property disclosed by this paper.
Extended data figures and tables
Extended Data Figure 1 Plot of potential versus current density at different rotation rates of the RDE.
The solution is 1 mM DHAQDS (1 mM in 1 M H2SO4), using a rotating disk electrode (RDE) of glassy carbon. Rotation rates are 200, 300, 400, 500, 700, 900, 1,200, 1,600, 2,000, 2,500 and 3,600 r.p.m.
Extended Data Figure 2 Levich and Koutecký–Levich plots obtained using the RDE.
a, Levich plot (limiting current versus square root of rotation rate ω) of 1 mM AQDS in 1 M H2SO4 (the fitted line has a slope of 4.53(2) µA s1/2 rad−1/2, giving D = 3.8(1) × 10−6 cm2 s−1). Data are an average of three runs; error bars indicate the standard deviation. b, As a but for DHAQDS in 1 M H2SO4 (slope of 3.94(6) µA s1/2 rad−1/2 gives D = 3.19(7) × 10−6 cm2 s−1). c, Koutecky–Levich plot (i−1 versus ω−1/2) of 1 mM DHAQDS in 1 M H2SO4. The current response, i, is shown for seven different AQDS reduction overpotentials η.
Extended Data Figure 3 Fit of Butler–Volmer equation.
Constructed using the current response in the absence of mass transport at low AQDS reduction overpotentials; iK is the current extrapolated from the zero-intercept of Fig. 3b and Extended Data Fig. 2c (infinite rotation rate). Data are an average of three runs; error bars indicate the standard deviation. a, AQDS: best-fit line has the equation y = 62(x + 4.32). This yields α = 0.474(2) and k0 = 7.2(5) × 10−3 cm s−1. b, DHAQDS: best-fit line is the function y = 68(x + 3.95). This yields α = 0.43(1) and k0 = 1.56(5) × 10−2 cm s−1.
Extended Data Figure 4 Pourbaix diagram (E0 vs pH) of AQDS.
Data are fitted to three solid lines indicating slopes of −59 mV pH−1, −30 mV pH−1 and 0 mV pH−1, corresponding to two-, one- and zero-proton processes, respectively. Dashed lines linearly extrapolate the one- and zero-proton processes to give E0 values of 18 mV (2e−/1H+) and −296 mV (2e−/0H+).
Extended Data Figure 5 1H NMR (500 MHz, D2O) spectra.
a, Spectrum of AQDS: chemical shift δ = 7.99 p.p.m. versus tetramethylsilane (TMS) (doublet (d), coupling constant J = 2 Hz, 1,8 C–H), 7.79 p.p.m. (doublet of doublets, J = 2 and 8 Hz, 4,5 C–H), 7.50 p.p.m. (d, J = 8 Hz, 3,6 C–H). b, The same sample, 20 h after addition of Br2. c, 1H NMR of AQDS treated with 2 M HBr and Br2 and heated to 100 °C for 48 h. The peaks are shifted due to presence of trace HBr, which shifted the residual solvent peak due to increased acidity. Coupling constants for each peak are identical to a.
Extended Data Figure 6 13C NMR (500 MHz, D2O) spectra.
a, AQDS, δ = 181.50 p.p.m. versus TMS (C 9), 181.30 p.p.m. (C 10), 148.51 p.p.m. (C 2,7), 133.16 p.p.m. (C 11), 132.40 p.p.m. (C 12), 130.86 p.p.m. (C 3,6), 128.59 p.p.m. (C 4,5), 124.72 p.p.m. (C 1,8). b, The same sample, 24 h after addition of Br2. c, 13C NMR of AQDS treated with 2 M HBr and Br2 and heated to 100 °C for 48 h.
Extended Data Figure 7 Calibration model for ΔHf and experimental E0.
This shows a linear relationship (red dashed line; R2 = 0.97) between calculated ΔHf (this work) and experimental E0 (from the literature) of six quinones in aqueous solutions: BQ, benzoquinone; NQ, naphthoquinone; AQ, anthraquinone; and PQ, phenanthraquinone.
Extended Data Figure 8 AQDS cyclic voltammograms.
Black curve, obtained for a 1 mM solution of AQDS in 1 M H2SO4 on a stationary glassy carbon working electrode. Red curve, obtained for a crude anthraquinone sulphonation solution containing a mixture of AQDS, 9,10-anthraquinone-2,6-disulphonic acid and 9,10-anthraquinone-2-sulphonic acid diluted to 1 mM total anthraquinone in 1 M H2SO4.
Extended Data Figure 9 Flow-battery cycling behaviour with HBr electrolyte on both sides.
Data collected by cycling the current at 0.2 A cm−2 at 40 °C using a 2 M HBr + 0.5 M Br2 solution on the positive side and a 2 M HBr + 0.1 M AQDS solution on the negative side; cell potential versus time performance is comparable to data in Fig. 2.
Rights and permissions
About this article
Cite this article
Huskinson, B., Marshak, M., Suh, C. et al. A metal-free organic–inorganic aqueous flow battery. Nature 505, 195–198 (2014). https://doi.org/10.1038/nature12909
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12909
This article is cited by
-
Recent Advances in Redox Flow Batteries Employing Metal Coordination Complexes as Redox-Active Species
Electrochemical Energy Reviews (2024)
-
Recent synthetic strategies of small heterocyclic organic molecules with optoelectronic applications: a review
Molecular Diversity (2024)
-
Deep learning workflow for the inverse design of molecules with specific optoelectronic properties
Scientific Reports (2023)
-
Near-frictionless ion transport within triazine framework membranes
Nature (2023)
-
Catholytes that mimic ionic liquids
Nature Energy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.