Abstract
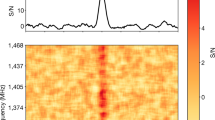
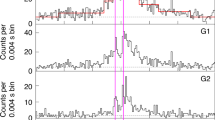
Earth’s nearest candidate supermassive black hole lies at the centre of the Milky Way1. Its electromagnetic emission is thought to be powered by radiatively inefficient accretion of gas from its environment2, which is a standard mode of energy supply for most galactic nuclei. X-ray measurements have already resolved a tenuous hot gas component from which the black hole can be fed3. The magnetization of the gas, however, which is a crucial parameter determining the structure of the accretion flow, remains unknown. Strong magnetic fields can influence the dynamics of accretion, remove angular momentum from the infalling gas4, expel matter through relativistic jets5 and lead to synchrotron emission such as that previously observed6,7,8. Here we report multi-frequency radio measurements of a newly discovered pulsar close to the Galactic Centre9,10,11,12 and show that the pulsar’s unusually large Faraday rotation (the rotation of the plane of polarization of the emission in the presence of an external magnetic field) indicates that there is a dynamically important magnetic field near the black hole. If this field is accreted down to the event horizon it provides enough magnetic flux to explain the observed emission—from radio to X-ray wavelengths—from the black hole.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
Change history
20 August 2013
Source Data files for Figs 1–3 were added.
References
Genzel, R., Eisenhauer, F. & Gillessen, S. The Galactic Center massive black hole and nuclear star cluster. Rev. Mod. Phys. 82, 3121–3195 (2010)
Narayan, R. & Yi, I. Advection-dominated accretion: a self-similar solution. Astrophys. J. 428, L13–L16 (1994)
Baganoff, F. K. et al. Chandra X-ray spectroscopic imaging of Sagittarius A* and the central parsec of the Galaxy. Astrophys. J. 591, 891–915 (2003)
Balbus, S. A. & Hawley, J. F. A powerful local shear instability in weakly magnetized disks. I - Linear analysis. II - Nonlinear evolution. Astrophys. J. 376, 214–233 (1991)
Beckwith, K., Hawley, J. F. & Krolik, J. H. The influence of magnetic field geometry on the evolution of black hole accretion flows: similar disks, drastically different jets. Astrophys. J. 678, 1180–1199 (2008)
Falcke, H. & Markoff, S. The jet model for Sgr A*: radio and X-ray spectrum. Astron. Astrophys. 362, 113–118 (2000)
Mościbrodzka, M., Gammie, C. F., Dolence, J. C., Shiokawa, H. & Leung, P. K. Radiative Models of Sgr A* from GRMHD simulations. Astrophys. J. 706, 497–507 (2009)
Dexter, J., Agol, E., Fragile, P. C. & McKinney, J. C. The submillimeter bump in Sgr A* from relativistic MHD simulations. Astrophys. J. 717, 1092–1104 (2010)
Kennea, J. A. et al. Swift Discovery of a new soft gamma repeater, SGR J1745–29, near Sagittarius A*. Astrophys. J. 770, L24 (2013)
Mori, K. et al. NuSTAR discovery of a 3.76 s transient magnetar near Sagittarius A*. Astrophys. J. 770, L23 (2013)
Eatough, R. P. et al. Detection of radio pulsations from the direction of the NuSTAR 3.76 second X-ray pulsar at 8.35 GHz. Astron. Telegr. 5040, 1 (2013)
Shannon, R. M. & Johnston, S. Radio properties of the magnetar near Sagittarius A* from observations with the Australia Telescope Compact Array. Preprint at http://arxiv.org/abs/1305.3036 (2013)
Bower, G. C., Falcke, H., Wright, M. C. & Backer, D. C. Variable linear polarization from Sagittarius A*: evidence of a hot turbulent accretion flow. Astrophys. J. 618, L29–L32 (2005)
Marrone, D. P., Moran, J. M., Zhao, J.-H. & Rao, R. An unambiguous detection of Faraday rotation in Sagittarius A*. Astrophys. J. 654, L57–L60 (2007)
Liu, K., Wex, N., Kramer, M., Cordes, J. M. & Lazio, T. J. W. Prospects for probing the spacetime of Sgr A* with pulsars. Astrophys. J. 747, 1 (2012)
Wharton, R. S., Chatterjee, S., Cordes, J. M., Deneva, J. S. & Lazio, T. J. W. Multiwavelength constraints on pulsar populations in the Galactic Center. Astrophys. J. 753, 108 (2012)
Eatough, R. P. et al. in Neutron Stars and Pulsars: Challenges and Opportunities After 80 Years (ed. Leeuwen, J. V. ) 382–384 (Cambridge Univ. Press, 2013)
Lazio, T. J. W. & Cordes, J. M. Hyperstrong radio-wave scattering in the Galactic Center. II. A likelihood analysis of free electrons in the Galactic Center. Astrophys. J. 505, 715–731 (1998)
Rea, N. et al. Chandra localization of the soft gamma repeater in the Galactic Center region. Astron. Telegr. 5032, 1 (2013)
Cordes, J. M. & Lazio, T. J. W. NE2001.I. A new model for the galactic distribution of free electrons and its fluctuations. Preprint at http://arxiv.org/abs/astroph/0207156 (2002)
Lazarus, P., Kaspi, V. M., Champion, D. J., Hessels, J. W. T. & Dib, R. Constraining radio emission from magnetars. Astrophys. J. 744, 97 (2012)
Lee, K. J. et al. Polarisation profiles and rotation measure of PSR J1745–2900 measured at Effelsberg. Astron. Telegr. 5064, 1 (2013)
Brentjens, M. A. & de Bruyn, A. G. Faraday rotation measure synthesis. Astron. Astrophys. 441, 1217–1228 (2005)
Law, C. J., Brentjens, M. A. & Novak, G. A constraint on the organization of the Galactic Center magnetic field using Faraday rotation. Astrophys. J. 731, 36 (2011)
Bower, G. C., Backer, D. C., Zhao, J.-H., Goss, M. & Falcke, H. The linear polarization of Sagittarius A*. I. VLA spectropolarimetry at 4.8 and 8.4 GHz. Astrophys. J. 521, 582–586 (1999)
Zhao, J.-H. et al. The high-density ionized gas in the central parsec of the Galaxy. Astrophys. J. 723, 1097–1109 (2010)
Plante, R. L., Lo, K. Y. & Crutcher, R. M. The magnetic fields in the galactic center: detection of H1 Zeeman splitting. Astrophys. J. 445, L113–L116 (1995)
Muno, M. P. et al. Diffuse X-ray emission in a deep Chandra image of the Galactic Center. Astrophys. J. 613, 326–342 (2004)
Macquart, J.-P., Bower, G. C., Wright, M. C. H., Backer, D. C. & Falcke, H. The rotation measure and 3.5 millimeter polarization of Sagittarius A*. Astrophys. J. 646, L111–L114 (2006)
Falcke, H., Mannheim, K. & Biermann, P. L. The galactic center radio jet. Astron. Astrophys. 278, L1–L4 (1993)
Acknowledgements
We wish to thank D. D. Xu., P. Lazarus and L. Guillemot for discussions. We also thank O. Wucknitz and R. Beck for reading the manuscript. R.K., L.G.S. and P.C.C.F. gratefully acknowledge financial support from the European Research Council for the ERC Starting Grant BEACON under contract no. 279702. K.J.L. was funded by ERC Advanced Grant LEAP under contract no. 227947. H.F. acknowledges funding from an Advanced Grant of the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 227610. This work was based on observations with the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg. The Nançay radio telescope is part of the Paris Observatory, associated with the Centre National de la Recherche Scientifique (CNRS), and partly supported by the Région Centre in France. The National Radio Astronomy Observatory (NRAO) is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc.
Author information
Authors and Affiliations
Contributions
R.P.E.: initial detections, observations performed at Effelsberg and data processing; H.F.: observational and theoretical background and paper formulation; R.K.: observational technical assistance and pulsar timing; K.J.L.: polarization and RM measurements; D.J.C.: pulsar timing solution; E.F.K.: flux density calculations, observational assistance and observations at Jodrell Bank; G.D.: observations at Nançay; D.H.F.M.S.: observational background and RM interpretation; L.G.S.: observational background and data processing and analysis; M.K.: observational background and RM interpretation; B.K.: technical observational assistance at Effelsberg; C.B.: observations at Jodrell Bank; G.C.B.: observations at the VLA and RM interpretation; A.B.: observations at the VLA; I.C.: observations at Nançay; A.T.D.: observations at the VLA; P.B.D.: observations at the VLA; P.C.C.F.: observational background and pulsar timing; A.K.: technical observational assistance at Effelsberg; A.G.L.: observations at Jodrell Bank and help with initial detections; A.N.: observational background and RM interpretation; B.S.: observations at Jodrell Bank; N.W.: theoretical background and orbital characteristics.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Eatough, R., Falcke, H., Karuppusamy, R. et al. A strong magnetic field around the supermassive black hole at the centre of the Galaxy. Nature 501, 391–394 (2013). https://doi.org/10.1038/nature12499
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12499
This article is cited by
-
Quasi-periodic sub-pulse structure as a unifying feature for radio-emitting neutron stars
Nature Astronomy (2023)
-
Overcharging process around a magnetized black hole: can the backreaction effect of magnetic field restore cosmic censorship conjecture?
General Relativity and Gravitation (2023)
-
A new model of quasar mass evolution
Astrophysics and Space Science (2022)
-
How to distinguish an actual astrophysical magnetized black hole mimicker from a true (theoretical) black hole
Astrophysics and Space Science (2021)
-
An X-ray chimney extending hundreds of parsecs above and below the Galactic Centre
Nature (2019)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.