Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Emergence of structural and dynamical properties of ecological mutualistic networks

Nature volume 500, pages 449–452 (2013)Cite this article

Subjects

Abstract

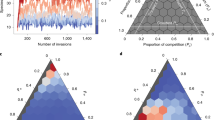
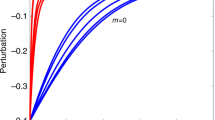
Mutualistic networks are formed when the interactions between two classes of species are mutually beneficial. They are important examples of cooperation shaped by evolution. Mutualism between animals and plants has a key role in the organization of ecological communities1,2,3. Such networks in ecology have generally evolved a nested architecture4,5 independent of species composition and latitude6,7; specialist species, with only few mutualistic links, tend to interact with a proper subset of the many mutualistic partners of any of the generalist species1. Despite sustained efforts5,8,9,10 to explain observed network structure on the basis of community-level stability or persistence, such correlative studies have reached minimal consensus11,12,13. Here we show that nested interaction networks could emerge as a consequence of an optimization principle aimed at maximizing the species abundance in mutualistic communities. Using analytical and numerical approaches, we show that because of the mutualistic interactions, an increase in abundance of a given species results in a corresponding increase in the total number of individuals in the community, and also an increase in the nestedness of the interaction matrix. Indeed, the species abundances and the nestedness of the interaction matrix are correlated by a factor that depends on the strength of the mutualistic interactions. Nestedness and the observed spontaneous emergence of generalist and specialist species occur for several dynamical implementations of the variational principle under stationary conditions. Optimized networks, although remaining stable, tend to be less resilient than their counterparts with randomly assigned interactions. In particular, we show analytically that the abundance of the rarest species is linked directly to the resilience of the community. Our work provides a unifying framework for studying the emergent structural and dynamical properties of ecological mutualistic networks2,5,10,14.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: The optimization principle.
Figure 2: Relationship between nestedness and species abundance.
Figure 3: Box–whisker plots of the degrees of nestedness for optimized networks.
Figure 4: Optimized networks are less resilient.

Similar content being viewed by others

References

  1. Pascual, M. & Dunne, J. Ecological Networks: Linking Structure to Dynamics in Food Webs (Oxford Univ. Press, 2006)

    MATH  Google Scholar 

  2. Montoya, J. M., Pimm, S. L. & Sole, R. V. Ecological networks and their fragility. Nature 442, 259–264 (2006)

    Article  ADS  CAS  Google Scholar 

  3. Bascompte, J. & Jordano, P. Plant–animal mutualistic networks: the architecture of biodiversity. Annu. Rev. Ecol. Evol. Syst. 38, 567–593 (2007)

    Article  Google Scholar 

  4. Almeida-Neto, M., Guimara, P., Guimara, P. R. & Ulrich, W. A consistent metric for nestedness analysis in ecological systems: reconciling concept and measurement. Oikos 117, 1227–1239 (2008)

    Article  Google Scholar 

  5. Bastolla, U. et al. The architecture of mutualistic networks minimizes competition and increases biodiversity. Nature 458, 1018–1020 (2009)

    Article  ADS  CAS  Google Scholar 

  6. Bascompte, J., Jordano, P., Melian, C. J. & Olesen, J. M. The nested assembly of plant–animal mutualistic networks. Proc. Natl Acad. Sci. USA 100, 9383–9387 (2003)

    Article  ADS  CAS  Google Scholar 

  7. Saavedra, S., Stouffer, D. B., Uzzi, B. & Bascompte, J. Strong contributors to network persistence are the most vulnerable to extinction. Nature 478, 233–235 (2011)

    Article  ADS  CAS  Google Scholar 

  8. Krishna, A., Guimara, P. R., Jordano, P. & Bascompte, J. A neutral-niche theory of nestedness in mutualistic networks. Oikos 117, 1609–1618 (2008)

    Article  Google Scholar 

  9. Okuyama, T. & Holland, J. N. Network structural properties mediate the stability of mutualistic communities. Ecol. Lett. 11, 208–216 (2008)

    Article  Google Scholar 

  10. Thébault, E. & Fontaine, C. Stability of ecological communities and the architecture of mutualistic and trophic networks. Science 329, 853–856 (2010)

    Article  ADS  Google Scholar 

  11. James, A., Pitchford, J. W. & Plank, M. J. Disentangling nestedness from models of ecological complexity. Nature 487, 227–230 (2012)

    Article  ADS  CAS  Google Scholar 

  12. Staniczenko, P. P., Kopp, J. C. & Allesina, S. The ghost of nestedness in ecological networks. Nature Commun. 4, 1391 (2013)

    Article  ADS  Google Scholar 

  13. Allesina, S. The more the merrier. Nature 487, 175–176 (2012)

    Article  ADS  CAS  Google Scholar 

  14. Allesina, S. & Tang, S. Stability criteria for complex ecosystems. Nature 483, 205–208 (2012)

    Article  ADS  CAS  Google Scholar 

  15. Campbell, C., Yang, S., Shea, K. & Albert, R. Topology of plant-pollinator networks that are vulnerable to collapse from species extinction. Phys. Rev. E 86, 021924 (2012)

    Article  ADS  Google Scholar 

  16. Thompson, A. R., Nisbet, R. M. & Schmitt, R. J. Dynamics of mutualist populations that are demographically open. J. Anim. Ecol. 75, 1239–1251 (2006)

    Article  Google Scholar 

  17. Holland, J. N., DeAngelis, D. L. & Bronstein, J. L. Population dynamics and mutualism: functional responses of benefits and costs. Am. Nat. 159, 231–244 (2002)

    Article  Google Scholar 

  18. Twardochleb, L. A. N. o. v. a. k. M. & Moore, J. W. Using the functional response of a consumer to predict biotic resistance to invasive prey. Ecol. Appl. 22, 1162–1171 (2012)

    Article  Google Scholar 

  19. Zhang, F., Hui, C. & Terblanche, J. S. An interaction switch predicts the nested architecture of mutualistic networks. Ecol. Lett. 14, 797–803 (2011)

    Article  Google Scholar 

  20. Douglas, M. W. Adaptation and habitat selection in the eco-evolutionary process. Proc. R. Soc. B 278, 2401–2411 (2011)

    Article  Google Scholar 

  21. McCann, K. S. The diversity–stability debate. Nature 405, 228–233 (2000)

    Article  CAS  Google Scholar 

  22. Ives, A. R. & Carpenter, S. R. Stability and diversity of ecosystems. Science 317, 58–62 (2007)

    Article  ADS  CAS  Google Scholar 

  23. Guimarães, P. R. et al. Interaction intimacy affects structure and coevolutionary dynamics in mutualistic networks. Curr. Biol. 17, 1797–1803 (2007)

    Article  Google Scholar 

  24. Guimarães, J., Jordano, P. & Thompson, J. N. Evolution and coevolution in mutualistic networks. Ecol. Lett. 14, 877–885 (2011)

    Article  Google Scholar 

  25. Nowak, M. A., Tarnita, C. E. & Wilson, E. O. The evolution of eusociality. Nature 466, 1057–1062 (2010)

    Article  ADS  CAS  Google Scholar 

  26. Nowak, M. A. Five rules for the evolution of cooperation. Science 314, 1560–1563 (2006)

    Article  ADS  CAS  Google Scholar 

  27. Ulrich, W., Almeida-Neto, W. & Gotelli, J. N. A consumer’s guide to nestedness analysis. Oikos 118, 3–17 (2009)

    Article  Google Scholar 

  28. Saavedra, S., Reed-Tsochas, F. & Uzzi, B. A simple model of bipartite cooperation for ecological and organizational networks. Nature 457, 463–466 (2009)

    Article  ADS  CAS  Google Scholar 

  29. May, R. M., Levin, S. A. & Sugihara, G. Complex systems: ecology for bankers. Nature 451, 893–895 (2008)

    Article  ADS  CAS  Google Scholar 

  30. Proulx, S. R., Promislow, D. E. & Phillips, P. C. Network thinking in ecology and evolution. Trends Ecol. Evol. 20, 345–353 (2005)

    Article  Google Scholar 

Download references

Acknowledgements

A.M. and S.S. acknowledge the Cariparo foundation for financial support. We thank S. Allesina, T. Cooke, J. Grilli and L. Mari for discussions and Studio 7 a.m. for graphics support.

Author information

Authors and Affiliations

  1. Dipartimento di Fisica e Astronomia ‘G. Galilei’ & CNISM, INFN, Università di Padova, Via Marzolo 8, 35131 Padova, Italy,

    Samir Suweis & Amos Maritan

  2. Center for Complex Network Research and Department of Physics, Biology and Computer Science, Northeastern University, Boston, 02115, Massachusetts, USA

    Filippo Simini

  3. Institute of Physics, Budapest University of Technology and Economics Budafoki ut 8, Budapest H-1111, Hungary,

    Filippo Simini

  4. Department of Physics, University of Maryland, College Park, 20742, Maryland, USA

    Jayanth R. Banavar

Authors
  1. Samir Suweis
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Filippo Simini
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Jayanth R. Banavar
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Amos Maritan
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

S.S. carried out the numerical calculations and the data analysis. All the authors contributed to other aspects of the paper.

Corresponding authors

Correspondence to Samir Suweis or Amos Maritan.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

This file contains Supplementary Methods and Discussions, Supplementary Figures 1-24 and additional references. The Supplementary Methods give the mathematical definition of nestedness and show how we have tuned the connectivity in our simulations. They also give details of the mathematical framework and optimization algorithm. All the analytical results presented in the main text are proved and the numerical simulations are explained in detail. In the Supplementary Discussions, we compare the result obtained by the Species-level Optimization, the Community-level Optimization and the Optimization while assembling the Community. Finally, we discuss the relationship between the total abundance of individuals in the community and the nestedness. See Contents for more details. (PDF 1086 kb)

PowerPoint slides

Rights and permissions

Reprints and permissions

About this article

Cite this article

Suweis, S., Simini, F., Banavar, J. et al. Emergence of structural and dynamical properties of ecological mutualistic networks. Nature 500, 449–452 (2013). https://doi.org/10.1038/nature12438

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature12438

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing