Abstract
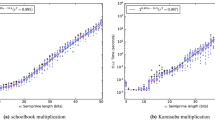
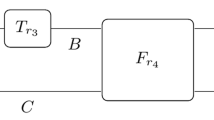
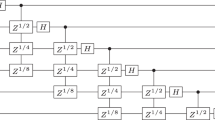
Shor’s quantum factoring algorithm exponentially outperforms known classical methods. Previous experimental implementations have used simplifications dependent on knowing the factors in advance. However, as we show here, all composite numbers admit simplification of the algorithm to a circuit equivalent to flipping coins. The difficulty of a particular experiment therefore depends on the level of simplification chosen, not the size of the number factored. Valid implementations should not make use of the answer sought.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Shor, P. W. in Proc. 35th IEEE Symp. on the Foundations of Computer Science (FOCS) 124–134 (IEEE Computer Society, 1994)
Shor, P. W. in Proc. 37th IEEE Symp. on the Foundations of Computing (FOCS) 56–65 (IEEE Computer Society, 1996)
Aliferis, P., Gottesman, D. & Preskill, J. Accuracy threshold for postselected quantum computation. Quant. Inform. Comput. 8, 181–244 (2008)
Zurek, W. H. Pointer basis of quantum apparatus: into what mixture does the wave packet collapse? Phys. Rev. D 24, 1516–1525 (1981)
Vandersypen, L. M. K. et al. Experimental realization of Shor’s quantum factoring algorithm using nuclear magnetic resonance. Nature 414, 883–887 (2001)
Lanyon, B. P. et al. Experimental demonstration of a compiled version of Shor’s algorithm with quantum entanglement. Phys. Rev. Lett. 99, 250505 (2007)
Lu, C.-Y., Browne, D. E., Yang, T. & Pan, J.-W. Demonstration of a compiled version of Shor’s quantum factoring algorithm using photonic qubits. Phys. Rev. Lett. 99, 250504 (2007)
Politi, A., Matthews, J. C. F. & O’Brien, J. L. Shor’s quantum factoring algorithm on a photonic chip. Science 325, 1221 (2009)
Martín-López, E., Laing, A., Lawson, T., Zhou, X.-Q. & O’Brien, J. L. Experimental realization of Shor’s quantum factoring algorithm using qubit recycling. Nature Photon. 6, 773–776 (2012)
Lucero, E. Computing prime factors with a Josephson phase qubit quantum processor. Nature Phys. 8, 719–723 (2012)
Lenstra, A. K., Lenstra, H. W., Jr, Manasse, M. S. & Pollard, J. M. in Proc. 22nd Annual ACM Symp. on Theory of Computing (STOC) 564–572 (ACM Press, New York, 1990)
Zalka, C. Shor’s algorithm with fewer (pure) qubits. Preprint at http://arXiv.org/abs/quant-ph/0601097 (2006)
Mosca, M. & Ekert, A. in Quantum Computing and Quantum Communications (ed. Williams, C. P. ) 174–188 (Vol. 1509, Lecture Notes in Computer Science, Springer, 1999)
Parker, S. & Plenio, M. B. Efficient factorization with a single pure qubit and logN mixed qubits. Phys. Rev. Lett. 85, 3049–3052 (2000)
Griffiths, R. B. & Niu, C. S. Semiclassical Fourier transform for quantum computation. Phys. Rev. Lett. 76, 3228–3231 (1996)
Zhou, Z. & Geller, M. R. Factoring 51 and 85 with 8 qubits. Preprint at http://arXiv.org/abs/1304.0128 (2013)
Zi, S. The mathematical classic of Sun Zi. In Yong, L.-L. & Se, A.-T. Fleeting Footsteps: Tracing the Conception of Arithmetic and Algebra in Ancient China (World Scientific, 2004)
Heath, T. (ed) The Thirteen Books of Euclid's Elements (Dover, 1956)
Acknowledgements
We acknowledge support from IARPA (contract no. W911NF-10-1-0324) and from the DARPA QUEST programme (contract no. HR0011-09-C-0047). All statements of fact, opinion or conclusions contained herein are those of the authors and should not be construed as representing the official views or policies of the US Government.
Author information
Authors and Affiliations
Contributions
J.A.S., G.S. and A.V. designed and carried out the research. G.S. performed the experiments, J.A.S. analysed the data, and A.V. carried out the number theory. J.A.S., G.S. and A.V. wrote the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains N-20000, a 20,000-bit number of our own creation. (PDF 96 kb)
Rights and permissions
About this article
Cite this article
Smolin, J., Smith, G. & Vargo, A. Oversimplifying quantum factoring. Nature 499, 163–165 (2013). https://doi.org/10.1038/nature12290
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature12290
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.