Abstract
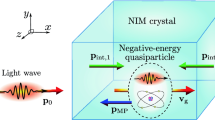
Metamaterials with negative refractive indices can manipulate electromagnetic waves in unusual ways, and can be used to achieve, for example, sub-diffraction-limit focusing1, the bending of light in the ‘wrong’ direction2, and reversed Doppler and Cerenkov effects2. These counterintuitive and technologically useful behaviours have spurred considerable efforts to synthesize a broad array of negative-index metamaterials with engineered electric, magnetic or optical properties1,2,3,4,5,6,7,8,9,10. Here we demonstrate another route to negative refraction by exploiting the inertia of electrons in semiconductor two-dimensional electron gases, collectively accelerated by electromagnetic waves according to Newton’s second law of motion, where this acceleration effect manifests as kinetic inductance11,12. Using kinetic inductance to attain negative refraction was theoretically proposed for three-dimensional metallic nanoparticles13 and seen experimentally with surface plasmons on the surface of a three-dimensional metal14. The two-dimensional electron gas that we use at cryogenic temperatures has a larger kinetic inductance than three-dimensional metals, leading to extraordinarily strong negative refraction at gigahertz frequencies, with an index as large as −700. This pronounced negative refractive index and the corresponding reduction in the effective wavelength opens a path to miniaturization in the science and technology of negative refraction.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Pendry, J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966–3969 (2000)
Veselago, V. G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. Usp. 10, 509–514 (1968)
Smith, D. R., Padilla, W. J., Vier, D. C., Nemat-Nasser, S. C. & Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 84, 4184–4187 (2000)
Shelby, R. A., Smith, D. R. & Schultz, S. Experimental verification of a negative index of refraction. Science 292, 77–79 (2001)
Linden, S. et al. Photonic metamaterials: magnetism at optical frequencies. IEEE J. Sel. Top. Quantum Electron. 12, 1097–1105 (2006)
Cubukcu, E., Aydin, K., Ozbay, E., Foteinopoulou, S. & Soukoulis, C. M. Electromagnetic waves: negative refraction by photonic crystals. Nature 423, 604–605 (2003)
Valentine, J. et al. Three-dimensional optical metamaterial with a negative refractive index. Nature 455, 376–379 (2008)
Podolskiy, V. A. & Narimanov, E. E. Strongly anisotropic waveguide as a nonmagnetic left-handed system. Phys. Rev. B 71, 201101 (2005)
Hoffman, A. J. et al. Negative refraction in semiconductor metamaterials. Nature Mater. 6, 946–950 (2007)
Pendry, J. B. A chiral route to negative refraction. Science 306, 1353–1355 (2004)
Meservey, R. Measurements of the kinetic inductance of superconducting linear structures. J. Appl. Phys. 40, 2028–2034 (1969)
Burke, P. J., Spielman, I. B., Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. High frequency conductivity of the high-mobility two-dimensional electron gas. Appl. Phys. Lett. 76, 745–747 (2000)
Engheta, N. Circuits with light at nanoscales: optical nanocircuits inspired by metamaterials. Science 317, 1698–1702 (2007)
Lezec, H. J., Dionne, J. A. & Atwater, H. A. Negative refraction at visible frequencies. Science 316, 430–432 (2007)
Eleftheriades, G. V., Iyer, A. K. & Kremer, P. C. Planar negative refractive index media using periodically L–C loaded transmission lines. IEEE Trans. Microw. Theory Tech. 50, 2702–2712 (2002)
Caloz, C. & Itoh, T. Transmission line approach of left-handed (LH) materials and microstrip implementation of an artificial LH transmission line. IEEE Trans. Antenn. Propag. 52, 1159–1166 (2004)
Grbic, A. & Eleftheriades, G. V. Overcoming the diffraction limit with a planar left-handed transmission-line lens. Phys. Rev. Lett. 92, 117403 (2004)
Stern, F. Polarizability of a two-dimensional electron gas. Phys. Rev. Lett. 18, 546–548 (1967)
Chen, X., Grzegorczyk, T. M., Wu, B.-I., Pacheco, J. & Kong, J. A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 70, 016608 (2004)
Smith, D. R., Vier, D. C., Koschny, T. & Soukoulis, C. M. Electromagnetic parameter retrieval from inhomogeneous metamaterials. Phys. Rev. E 71, 036617 (2005)
Burgos, S. P., de Waele, R., Polman, A. & Atwater, H. A. A single-layer wide-angle negative-index metamaterial at visible frequencies. Nature Mater. 9, 407–412 (2010)
Choi, M. et al. A terahertz metamaterial with unnaturally high refractive index. Nature 470, 369–373 (2011)
Chanda, D. et al. Large-area flexible 3D optical negative index metamaterial formed by nanotransfer printing. Nature Nanotechnol. 6, 402–407 (2011)
Shalaev, V. M. Optical negative-index metamaterials. Nature Photon. 1, 41–48 (2007)
Soukoulis, C. M., Linden, S. & Wegener, M. Negative refractive index at optical wavelengths. Science 315, 47–49 (2007)
Meziani, Y. M. et al. Room temperature terahertz emission from grating coupled two-dimensional plasmons. Appl. Phys. Lett. 92, 201108 (2008)
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nature Nanotechnol. 5, 722–726 (2010)
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nature Nanotechnol. 6, 630–634 (2011)
Marks, R. B. A multiline method of network analyzer calibration. IEEE Trans. Microw. Theory Tech. 39, 1205–1215 (1991)
Andress, W. F. et al. Ultra-subwavelength two-dimensional plasmonic circuits. Nano Lett. 12, 2272–2277 (2012)
Acknowledgements
The authors are grateful for support for this research by the Air Force Office of Scientific Research under contract numbers FA 9550-09-1-0369 and FA 9550-08-1-0254. Device fabrication was performed in part at the Center for Nanoscale Systems at Harvard University. The authors thank W. F. Andress for assistance with device fabrication and microwave measurements.
Author information
Authors and Affiliations
Contributions
H.Y. and D.H. had the idea for the project. V.U. fabricated the 2DEG. H.Y. designed, fabricated and measured the properties of the devices. H.Y., K.Y.M.Y. and D.H. analysed the data. H.Y. and D.H. wrote the paper. All authors discussed the results and reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data, Supplementary Figures 1-10, Supplementary Tables 1-2 and additional references. (PDF 1642 kb)
Rights and permissions
About this article
Cite this article
Yoon, H., Yeung, K., Umansky, V. et al. A Newtonian approach to extraordinarily strong negative refraction. Nature 488, 65–69 (2012). https://doi.org/10.1038/nature11297
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature11297
This article is cited by
-
Implementing fractional Fourier transform and solving partial differential equations using acoustic computational metamaterials in space domain
Acta Mechanica Sinica (2021)
-
Extraordinary wavelength reduction in terahertz graphene-cladded photonic crystal slabs
Scientific Reports (2016)
-
Measurement of collective dynamical mass of Dirac fermions in graphene
Nature Nanotechnology (2014)
-
Induced transparency by coupling of Tamm and defect states in tunable terahertz plasmonic crystals
Nature Photonics (2013)
-
Ultrafast refractive index control of a terahertz graphene metamaterial
Scientific Reports (2013)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.