Abstract
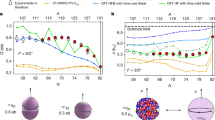
Nucleonic matter displays a quantum-liquid structure, but in some cases finite nuclei behave like molecules composed of clusters of protons and neutrons. Clustering is a recurrent feature in light nuclei, from beryllium to nickel1,2,3. Cluster structures are typically observed as excited states close to the corresponding decay threshold; the origin of this phenomenon lies in the effective nuclear interaction, but the detailed mechanism of clustering in nuclei has not yet been fully understood. Here we use the theoretical framework of energy-density functionals4,5, encompassing both cluster and quantum liquid-drop aspects of nuclei, to show that conditions for cluster formation can in part be traced back to the depth of the confining nuclear potential. For the illustrative example of neon-20, we show that the depth of the potential determines the energy spacings between single-nucleon orbitals in deformed nuclei, the localization of the corresponding wavefunctions and, therefore, the degree of nucleonic density clustering. Relativistic functionals, in particular, are characterized by deep single-nucleon potentials. When compared to non-relativistic functionals that yield similar ground-state properties (binding energy, deformation, radii), they predict the occurrence of much more pronounced cluster structures. More generally, clustering is considered as a transitional phenomenon between crystalline and quantum-liquid phases of fermionic systems.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Weizsäcker, C. F. V. Neuere Modellvorstellungen über den Bau der Atomkerne. Naturwissenschaften 26, 209–217 (1938)
Wheeler, J. A. On the mathematical description of light nuclei by the method of resonating group structure. Phys. Rev. 52, 1107–1122 (1937)
Von Oertzen, W. V., Freer, M. & Kanada-En’yo, Y. Nuclear clusters and nuclear molecules. Phys. Rep. 432, 43–113 (2006)
Bender, M., Heenen, P.-H. & Reinhard, P.-G. Self-consistent mean-field models for nuclear structure. Rev. Mod. Phys. 75, 121–180 (2003)
Vretenar, D., Afanasjev, A. V., Lalazissis, G. A. & Ring, P. Relativistic Hartree−Bogoliubov theory: static and dynamic aspects of exotic nuclear structure. Phys. Rep. 409, 101–259 (2005)
Kanada-En’yo, Y. & Horiuchi, H. Structure of light unstable nuclei studied with antisymmetrized molecular dynamics. Prog. Theor. Phys. 142 (Suppl.). 205–263 (2001)
Feldmeier, H., Bieler, K. & Schnack, J. Fermionic molecular dynamics for ground states and collision of nuclei. Nucl. Phys. A 586, 493–532 (1995)
Neff, T. & Feldmeier, H. Tensor correlations in the unitary correlation operator method. Nucl. Phys. A 713, 311–371 (2003)
Tohsaki, A., Horiuchi, H., Schuck, P. & Röpke, G. Alpha cluster condensation in 12C and 16O. Phys. Rev. Lett. 87, 192501 (2001)
Fynbo, H. O. U. et al. Revised rates for the stellar triple-α process from measurement of 12C nuclear resonances. Nature 433, 136–139 (2005)
Rose, H. J. & Jones, G. A. A new kind of natural radioactivity. Nature 307, 245–247 (1984)
Greiner, W., Park, J. Y. & Scheid, W. Nuclear Molecules (World Scientific, 1995)
Ikeda K, Tagikawa N & Horiuchi H The systematic structure-change into the molecule-like structures in the self-conjugate 4n nuclei. Prog. Theor. Phys. 464 (Suppl.). 464–475 (1968)
Arumugam, P., Sharma, B. K. & Patra, S. K. Relativistic mean field study of clustering in light nuclei. Phys. Rev. C 71, 064308 (2005)
Maruhn, J. A. et al. α-Cluster structure and exotic states in a self-consistent model for light nuclei. Phys. Rev. C 74, 044311 (2006)
Reinhard, P.-G., Maruhn, J. A., Umar, A. S. & Oberacker, V. E. Localization in light nuclei. Phys. Rev. C 83, 034312 (2011)
Okolowicz, J., Ploszajczak, M. & Nazarewicz, W. On the origin of nuclear clustering. Preprint at 〈http://arxiv.org/abs/1202.6290〉 (2012)
Girod, M. & Grammaticos, B. Triaxial Hartree−Fock−Bogolyubov calculations with D1 effective interaction. Phys. Rev. C 27, 2317–2339 (1983)
Ichikawa, T., Marhun, J. A., Itagaki, N. & Ohkubo, S. Linear chain structure of four-α clusters in 16O. Phys. Rev. Lett. 107, 112501 (2011)
Robledo, L. M. & Bertsch, G. F. Global systematics of octupole excitations in even−even nuclei. Phys. Rev. C 84, 054302 (2011)
Chabanat, E., Bonche, P., Haensel, P., Meyer, J. & Schaeffer, R. A Skyrme parametrization from subnuclear to neutron star densities part II. Nuclei far from stabilities. Nucl. Phys. A 635, 231–256 (1998)
Lalazissis, G. A., Nikšić, T., Vretenar, D. & Ring, P. New relativistic mean-field interaction with density-dependent meson-nucleons couplings. Phys. Rev. C 71, 024312 (2005)
Fricke, G. et al. Behavior of the nuclear charge radii systematics in the s-d shell from muonic atom measurement. Phys. Rev. C 45, 80–89 (1992)
Chulkov, L. et al. Interaction cross sections and matter radii of A = 20 isobars. Nucl. Phys. A 603, 219–237 (1996)
Nilsson, S. G. Binding states of individual nucleons in strongly deformed nuclei Mat. Fys. Medd. Dan. Vid. Selsk. 29, 1–69 (1955)
Cohen-Tannoudji, C., Diu, B. & Laloë, F. Mécanique Quantique (Hermann Ed., 1973)
Walecka, J. D. Theoretical Nuclear and Subnuclear Physics (Imperial College Press and World Scientific, 2004)
Mottelson, B. Elementary features of nuclear structure. In Les Houches Session LXVI, Trends in Nuclear Physics, 100 Years Later (eds Nifenecker, H., Blaizot, J.-P., Bertsch, G. F., Weise, W. & David, F. ). 25–121 (North-Holland Elsevier, 1996)
Pines, D. & Nozières, P. The theory of quantum liquids (Benjamin, 1966)
Stoitsov, M. V., Dobaczewski, J., Nazarewicz, W. & Ring, P. Axially deformed solution of the Skyrme−Hartree−Fock−Bogolyubov equations using the transformed harmonic oscillator basis. The program HFBTHO (v1.66p). Comput. Phys. Commun. 167, 43–63 (2005)
Acknowledgements
This work was supported by the Institut Universitaire de France and by the Croatian Ministry of Science, Education and Sport—project 1191005-1010. The authors thank J. Margueron, M. Milin, T. Neff, N. Van Giai and P. Schuck for comments and suggestions.
Author information
Authors and Affiliations
Contributions
Model calculations were done by J.-P.E., E.K., T.N. and D.V. The manuscript text was prepared by E.K. and D.V. with contributions from J.-P.E. and T.N. J.-P.E. and E.K. prepared the figures.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Rights and permissions
About this article
Cite this article
Ebran, JP., Khan, E., Nikšić, T. et al. How atomic nuclei cluster. Nature 487, 341–344 (2012). https://doi.org/10.1038/nature11246
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature11246
This article is cited by
-
New extended method for ψ′ scaling function of inclusive electron scattering
Science China Physics, Mechanics & Astronomy (2023)
-
Research on two-proton radioactivity in density-dependent cluster model
Science China Physics, Mechanics & Astronomy (2023)
-
The interplay of single-particle and collective motions in the low-lying states of \(_\Lambda ^{21}\) with quadrupole-octupole correlations
Science China Physics, Mechanics & Astronomy (2023)
-
α-Clustering in atomic nuclei from first principles with statistical learning and the Hoyle state character
Nature Communications (2022)
-
Nucleon momentum distribution of 56Fe from the axially deformed relativistic mean-field model with nucleon-nucleon correlations
Science China Physics, Mechanics & Astronomy (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.