Abstract
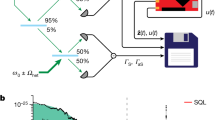
Feedback loops are central to most classical control procedures. A controller compares the signal measured by a sensor (system output) with the target value or set-point. It then adjusts an actuator (system input) to stabilize the signal around the target value. Generalizing this scheme to stabilize a micro-system’s quantum state relies on quantum feedback1,2,3, which must overcome a fundamental difficulty: the sensor measurements cause a random back-action on the system. An optimal compromise uses weak measurements4,5, providing partial information with minimal perturbation. The controller should include the effect of this perturbation in the computation of the actuator’s operation, which brings the incrementally perturbed state closer to the target. Although some aspects of this scenario have been experimentally demonstrated for the control of quantum6,7,8,9 or classical10,11 micro-system variables, continuous feedback loop operations that permanently stabilize quantum systems around a target state have not yet been realized. Here we have implemented such a real-time stabilizing quantum feedback scheme12 following a method inspired by ref. 13. It prepares on demand photon number states (Fock states) of a microwave field in a superconducting cavity, and subsequently reverses the effects of decoherence-induced field quantum jumps14,15,16. The sensor is a beam of atoms crossing the cavity, which repeatedly performs weak quantum non-demolition measurements of the photon number14. The controller is implemented in a real-time computer commanding the actuator, which injects adjusted small classical fields into the cavity between measurements. The microwave field is a quantum oscillator usable as a quantum memory17 or as a quantum bus swapping information between atoms18. Our experiment demonstrates that active control can generate non-classical states of this oscillator and combat their decoherence15,16, and is a significant step towards the implementation of complex quantum information operations.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Wiseman, H. M. Quantum theory of continuous feedback. Phys. Rev. A 49, 2133–2150 (1994)
Doherty, A. C., Habib, S., Jacobs, K., Mabuchi, H. & Tan, S. M. Quantum feedback control and classical control theory. Phys. Rev. A 62, 012105 (2000)
Wiseman, H. M. & Milburn, G. J. Quantum Measurement and Control (Cambridge Univ. Press, 2009)
Aharonov, Y. & Vaidman, L. Properties of a quantum system during the time interval between two measurements. Phys. Rev. A 41, 11–20 (1990)
Peres, A. & Wootters, W. K. Optimal detection of quantum information. Phys. Rev. Lett. 66, 1119–1122 (1991)
Nelson, R. J., Weinstein, Y., Cory, D. & Lloyd, S. Experimental demonstration of fully coherent quantum feedback. Phys. Rev. Lett. 85, 3045–3048 (2000)
Smith, W. P., Reiner, J. E., Orozco, L. A., Kuhr, S. & Wiseman, H. M. Capture and release of a conditional state of a cavity QED system by quantum feedback. Phys. Rev. Lett. 89, 133601 (2002)
Cook, R. L., Martin, P. J. & Geremia, J. M. Optical coherent state discrimination using a closed-loop quantum measurement. Nature 446, 774–777 (2007)
Gillett, G. G. et al. Experimental feedback control of quantum systems using weak measurements. Phys. Rev. Lett. 104, 080503 (2010)
Bushev, P. et al. Feedback cooling of a single trapped ion. Phys. Rev. Lett. 96, 043003 (2006)
Kubanek, A. et al. Photon-by-photon feedback control of a single-atom trajectory. Nature 462, 898–901 (2009)
Dotsenko, I. et al. Quantum feedback by discrete quantum nondemolition measurements: Towards on-demand generation of photon-number states. Phys. Rev. A 80, 013805 (2009)
Geremia, J. M. Deterministic and nondestructively verifiable preparation of photon number states. Phys. Rev. Lett. 97, 073601 (2006)
Guerlin, C. et al. Progressive field-state collapse and quantum non-demolition photon counting. Nature 448, 889–893 (2007)
Brune, M. et al. Process tomography of field damping and measurement of Fock state lifetimes by quantum nondemolition photon counting in a cavity. Phys. Rev. Lett. 101, 240402 (2008)
Wang, H. et al. Measurement of the decay of Fock states in a superconducting quantum circuit. Phys. Rev. Lett. 101, 240401 (2008)
Maître, X. et al. Quantum memory with a single photon in a cavity. Phys. Rev. Lett. 79, 769–772 (1997)
Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565–582 (2001)
Glauber, R. J. Coherent and incoherent states of the radiation field. Phys. Rev. 131, 2766–2788 (1963)
Varcoe, B. T. H., Brattke, S., Weidinger, M. & Walther, H. Preparing pure photon number states of the radiation field. Nature 403, 743–746 (2000)
Hofheinz, M. et al. Generation of Fock states in a superconducting quantum circuit. Nature 454, 310–314 (2008)
Hofheinz, M. et al. Synthesizing arbitrary quantum states in a superconducting resonator. Nature 459, 546–549 (2009)
Haroche, S. & Raimond, J. M. Exploring the Quantum: Atoms, Cavities and Photons (Oxford Univ. Press, 2006)
Khalil, H. K. Nonlinear Systems (Prentice Hall, 2001)
Steane, A. M. Error correcting codes in quantum theory. Phys. Rev. Lett. 77, 793–797 (1996)
Lu, C.-Y. et al. Experimental quantum coding against qubit loss error. Proc. Natl Acad. Sci. USA 105, 11050–11054 (2008)
Schindler, P. et al. Experimental repetitive quantum error correction. Science 332, 1059–1061 (2011)
Knill, E., Laflamme, R., Martinez, R. & Negrevergne, C. Benchmarking quantum computers: the five-qubit error correcting code. Phys. Rev. Lett. 86, 5811–5814 (2001)
DiCarlo, L. et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit. Nature 467, 574–578 (2010)
Vitali, D., Zippili, S., Tombesi, P. & Raimond, J. M. Decoherence control with fully quantum feedback schemes. J. Mod. Opt. 51, 799–809 (2004)
Acknowledgements
This work was supported by the Agence Nationale de la Recherche (ANR) under the projects QUSCO-INCA, EPOQ2 and CQUID, and by the EU under the IP project AQUTE and ERC project DECLIC.
Author information
Authors and Affiliations
Contributions
C.S. and I.D. contributed equally to this work. Experimental work was carried out by C.S., I.D., X.Z., B.P., T.R., S.G., M.B., J.-M.R. and S.H., with major contributions from C.S., I.D. and X.Z.; P.R., M.M. and H.A. contributed to the design and optimization of the feedback control.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This file contains Supplementary Text and Data 1-5, Supplementary Figures 1- 7 with legends and additional references. (PDF 1034 kb)
Supplementary Movie 1
Quantum feedback trajectory stabilizing a 2-photon state - the movie shows the evolution of the density matrix estimated by the controller during the feedback trajectory presented in the left panel of Fig. 2. The movie also features the evolution of the photon-number distribution for photon numbers from 0 to 7. Each movie frame corresponds to 2 feedback iterations. (MOV 2905 kb)
Supplementary Movie 2
Quantum feedback trajectory stabilizing a 3-photon state - the movie shows the evolution of the density matrix estimated by the controller during the feedback trajectory presented in the right panel of Fig. 2. The movie also features the evolution of the photon-number distribution for photon numbers from 0 to 7. Each movie frame corresponds to 2 feedback iterations. (MOV 3123 kb)
Supplementary Movie 3
Open-loop quantum feedback trajectory - if no control injection is applied, the initial coherent field is rapidly converted into a mixture of photon number states. It then relaxes to vacuum while undergoing a series of quantum jumps (MOV 2817 kb)
Rights and permissions
About this article
Cite this article
Sayrin, C., Dotsenko, I., Zhou, X. et al. Real-time quantum feedback prepares and stabilizes photon number states. Nature 477, 73–77 (2011). https://doi.org/10.1038/nature10376
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature10376
This article is cited by
-
Real-time two-axis control of a spin qubit
Nature Communications (2024)
-
Unravelling-based (auto)control of back-action in atomic Bose–Einstein condensate
Frontiers of Physics (2024)
-
Preparing quantum states by measurement-feedback control with Bayesian optimization
Frontiers of Physics (2023)
-
Quantum Uncertainty Dynamics
Foundations of Physics (2023)
-
Real-Time Optimal State Estimation-Based Feedback Control for Stochastic Quantum Systems in the Non-Markovian Case
Journal of Systems Science and Complexity (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.