Abstract
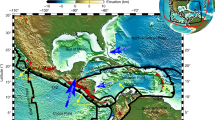
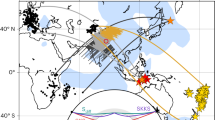
The direction of tectonic plate motion at the Earth’s surface and the flow field of the mantle inferred from seismic anisotropy are well correlated globally, suggesting large-scale coupling between the mantle and the surface plates1,2. The fit is typically poor at subduction zones, however, where regional observations of seismic anisotropy suggest that the direction of mantle flow is not parallel to3,4,5,6,7 and may be several times faster than6 plate motions. Here we present three-dimensional numerical models of buoyancy-driven deformation with realistic slab geometry for the Alaska subduction–transform system and use them to determine the origin of this regional decoupling of flow. We find that near a subduction zone edge, mantle flow velocities can have magnitudes of more than ten times the surface plate motions, whereas surface plate velocities are consistent with plate motions8 and the complex mantle flow field is consistent with observations from seismic anisotropy5. The seismic anisotropy observations constrain the shape of the eastern slab edge and require non-Newtonian mantle rheology. The incorporation of the non-Newtonian viscosity9,10 results in mantle viscosities of 1017 to 1018 Pa s in regions of high strain rate (10-12 s-1), and this low viscosity enables the mantle flow field to decouple partially from the motion of the surface plates. These results imply local rapid transport of geochemical signatures through subduction zones and that the internal deformation of slabs decreases the slab-pull force available to drive subducting plates.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Becker, T. W., Kellogg, J. B., Ekstrom, G. & O’Connell, R. J. Comparison of azimuthal seismic anisotropy from surface waves and finite strain from global mantle-circulation models. Geophys. J. Int. 155, 696–714 (2003)
Conrad, C. P., Behn, M. D. & Silver, P. G. Global mantle flow and the development of seismic anisotropy: differences between the oceanic and continental upper mantle. J. Geophys. Res. 112, B07317 (2007)
Russo, R. M. & Silver, P. G. Trench-parallel flow beneath the Nazca Plate from seismic anisotropy. Science 263, 1105–1111 (1994)
Smith, G. P. et al. A complex pattern of mantle flow in the Lau backarc. Science 292, 713–716 (2001)
Christensen, D. H. & Abers, G. A. Seismic anisotropy under central Alaska from SKS splitting observations. J. Geophys. Res. 115, BO4315 (2010)
Hoernle, K. et al. Arc-parallel flow in the mantle wedge beneath Costa Rica and Nicaragua. Nature 451, 1094–1097 (2008)
Long, M. & Silver, P. G. The subduction zone flow field from seismic anisotropy: a global view. Science 319, 315–318 (2008)
DeMets, C. & Dixon, T. H. New kinematic models for Pacific-North American motion from 3 Ma to present: evidence for steady state motion and biases in the NUVEL-1A model. Geophys. Res. Lett. 26, 1921–1924 (1999)
Hirth, G. & Kohlstedt, D. in Inside the Subduction Factory (ed. Eiler, J.) 83–105 (American Geophysical Union, 2003)
Karato, S., Jung, H., Katayama, I. & Skemer, P. Geodynamic significance of seismic anisotropy of the upper mantle: new insights from laboratory studies. Annu. Rev. Earth Planet. Sci. 36, 59–95 (2008)
Savage, M. K. Seismic anisotropy and mantle deformation: what have we learned from shear wave splitting? Rev. Geophys. 374, 65–106 (1999)
Kaminiski, É. & Ribe, N. M. Timescales for the evolution of seismic anisotropy in mantle flow. Geochem. Geophys. Geosyst. 3, 1051 (2002)
Peyton, V. et al. Mantle flow at a slab edge: seismic anisotropy in the Kamchatka region. Geophys. Res. Lett. 28, 379–382 (2001)
Zhong, S. & Gurnis, M. Interaction of weak faults and non-Newtonian rheology produces plate tectonics in a 3D model of mantle flow. Nature 383, 245–247 (1996)
Zhong, S., Gurnis, M. & Moresi, L. Role of faults, nonlinear rheology, and viscosity structure in generating plates from instantaneous mantle flow models. J. Geophys. Res. 103, 15255–15268 (1998)
Schellart, W. P. Kinematics of subduction and subduction-induced flow in the upper mantle. J. Geophys. Res. 109, B07401 (2004)
Funiciello, F. et al. Mapping mantle flow during retreating subduction: laboratory models analyzed by feature tracking. J. Geophys. Res. 111, B03402 (2006)
Piromallo, C., Becker, T. W., Funiciello, F. & Faccenna, C. Three-dimensional instantaneous mantle flow induced by subduction. Geophys. Res. Lett. 33, L08304 (2006)
Stegman, D. R., Freeman, J., Schellart, W. P., Moresi, L. & May, D. Influence of trench width on subduction hinge retreat rates in 3-D models of slab rollback. Geochem. Geophys. Geosyst. 7, Q03012 (2006)
Kneller, E. A. & van Keken, P. E. Trench-parallel flow and seismic anisotropy in the Mariana and Andean subduction systems. Nature 450, 1222–1225 (2007)
Garfunkel, Z., Anderson, C. A. & Schubert, G. Mantle circulation and the lateral migration of subducted slabs. J. Geophys. Res. 91, 7205–7223 (1986)
Billen, M. I. & Hirth, G. Rheologic controls on slab dynamics. Geochem. Geophys. Geosyst. 8, Q08012 (2007)
Lallemand, S. E., Heuret, A. & Boutelier, D. On the relationships between slab dip, back-arc stress, upper plate absolute motion and crustal nature in subduction zones. Geochem. Geophys. Geosyst. 6, Q09006 (2005)
Preece, S. J. & Hart, W. K. Geochemical variations in the 5 Ma Wrangell Volcanic Field, Alaska: implications for the magmatic and tectonic development of a complex continental arc system. Tectonophysics 392, 165–191 (2004)
Turner, S., Bourdon, B. & Gill, J. Insights into magma genesis at convergent margins from U-series isotopes. Rev. Mineral. Geochem. 52, 255–315 (2003)
Conder, J. A., Wiens, D. A. & Morries, J. On the decompression melting structure at volcanic arcs and back-arc spreading centers. Geophys. Res. Lett. 29 10.1029/2002GL015390 (2002)
Conrad, C. P. & Lithgow-Bertelloni, C. How mantle slabs drive plate tectonics. Science 298, 207–209 (2002)
Zhong, S. Constraints on thermochemical convection of the mantle from plume heat flux, plume excess temperature and upper mantle temperature. J. Geophys. Res. 111, B04409 (2006)
Moresi, L. & Gurnis, M. Constraints on the lateral strength of slabs from three-dimensional dynamic flow models. Earth Planet. Sci. Lett. 138, 15–28 (1996)
Müller, R. D., Roest, W. R., Royer, J. Y., Gahagan, L. M. & Sclater, J. G. Digital isochrons of the world’s ocean floor. J. Geophys. Res. 102, 3211–3214 (1997)
Turcotte, D. L. & Schubert, G. Geodynamics 2nd edn, 153–161 (Cambridge Univ. Press, 2002)
Kohlstedt, D. L., Evans, B. & Mackwell, S. J. Strength of the lithosphere: constraints imposed by laboratory experiments. J. Geophys. Res. 100, 17587–17602 (1995)
Moresi, L. N. & Solomatov, V. S. Numerical investigations of two-dimensional convection with extremely large viscosity variations. Phys. Fluids 9, 2142–2162 (1995)
Moresi, L., Zhong, S. & Gurnis, M. The accuracy of finite element solutions of Stokes’ flow with strongly varying viscosity. Earth Planet. Sci. Lett. 97, 83–94 (1996)
Jadamec, M. A. Three-Dimensional Lithosphere and Mantle Dynamics: Models of the Subduction-Transform Plate Boundary System in Southern Alaska. PhD thesis, Univ. California, Davis (2009)
Zandt, G. & Humphreys, E. Toroidal mantle flow through the western U.S. slab window. Geology 36, 295–298 (2008)
Lassak, T. M., Fouch, M. J. & Kaminiski, É. Seismic characterization of mantle flow in subduction systems: can we resolve a hydrated mantle wedge? Earth Planet. Sci. Lett. 243, 632–649 (2006)
Acknowledgements
This work was supported by US National Science Foundation grant EAR-0537995. High-resolution models were run on the TeraGrid cluster Lonestar at the Texas Advanced Computing Center, through grant TG-EAR080015N. We thank Computational Infrastructure for Geodynamics for the CitcomCU source code and C. Conrad and M. Behn for the source code used to calculate the ISAs. 3D data were visualized at the W. M. Keck Center for Active Visualization in the Earth Sciences at the University of California, Davis. We thank D. Christensen and G. Abers (shear-wave splitting data) and N. Ruppert (earthquake hypocentral data). We thank D. Turcotte, L. Kellogg, O. Kreylos, D. Eberhart-Phillips, S. M. Roeske, J. Dewey, T. Taylor, L. Moresi and G. Hirth for comments and discussions.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to the overall development of the project, model design considerations, analysis and interpretations. M.A.J. performed all of the numerical modelling, except for the ISA calculations, which were done by M.I.B.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing financial interests.
Supplementary information
Supplementary Information
This files contains Supplementary Notes comprising Model design; Slab structure; Thermal structure; Rheology; Model results; Pacific plate motion and Comparisons of ISA and SKS; Supplementary Figures 1-8 with legends; Supplementary Tables 1-4 and References. (PDF 2775 kb)
Rights and permissions
About this article
Cite this article
Jadamec, M., Billen, M. Reconciling surface plate motions with rapid three-dimensional mantle flow around a slab edge. Nature 465, 338–341 (2010). https://doi.org/10.1038/nature09053
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature09053
This article is cited by
-
Influence of the asthenosphere on earth dynamics and evolution
Scientific Reports (2023)
-
Role of subduction dynamics on the unevenly distributed volcanism at the Middle American subduction system
Scientific Reports (2023)
-
Three-dimensional variations of the slab geometry correlate with earthquake distributions at the Cascadia subduction system
Nature Communications (2018)
-
A subduction and mantle plume origin for Samoan volcanism
Scientific Reports (2018)
-
South-American plate advance and forced Andean trench retreat as drivers for transient flat subduction episodes
Nature Communications (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.