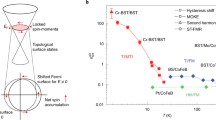
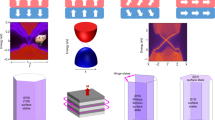
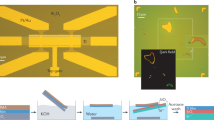
Abstract
Certain insulators have exotic metallic states on their surfaces. These states are formed by topological effects that also render the electrons travelling on such surfaces insensitive to scattering by impurities. Such topological insulators may provide new routes to generating novel phases and particles, possibly finding uses in technological applications in spintronics and quantum computing.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Haldane, F. D. M. Model for a quantum Hall effect without Landau levels: condensed-matter realization of the 'parity anomaly'. Phys. Rev. Lett. 61, 2015–2018 (1988).
Murakami, S., Nagaosa, N. & Zhang, S.-C. Spin-Hall insulator. Phys. Rev. Lett. 93, 156804 (2004).
Kane, C. L. & Mele, E. J. Z2 topological order and the quantum spin Hall effect. Phys. Rev. Lett. 95, 146802 (2005). This paper explains the theoretical requirements for a non-magnetic material to be a 2D topological insulator, with a quantum spin Hall effect.
Bernevig, B. A., Hughes, T. L. & Zhang, S.-C. Quantum spin Hall effect and topological phase transition in HgTe quantum wells. Science 314, 1757–1761 (2006).
König, M. et al. Quantum spin Hall insulator state in HgTe quantum wells. Science 318, 766–770 (2007). This paper reports the first experimental observation of a 2D topological insulator that has a quantum spin Hall effect.
Fu, L., Kane, C. L. & Mele, E. J. Topological insulators in three dimensions. Phys. Rev. Lett. 98, 106803 (2007).
Moore, J. E. & Balents, L. Topological invariants of time-reversal-invariant band structures. Phys. Rev. B 75, 121306(R) (2007).
Roy, R. Topological phases and the quantum spin Hall effect in three dimensions. Phys. Rev. B 79, 195322 (2009).
Ran, Y., Zhang, Y. & Vishwanath, A. One-dimensional topologically protected modes in topological insulators with lattice dislocations. Nature Phys. 5, 298–303 (2009).
Hsieh, D. et al. A topological Dirac insulator in a quantum spin Hall phase. Nature 452, 970–974 (2008). By using ARPES experiments, this study observed a 3D topological insulator, the theoretical predictions for which were made in refs 6,7,8.
Hsieh, D. et al. Observation of unconventional quantum spin textures in topological insulators. Science 323, 919–922 (2009).
Xia, Y. et al. Observation of a large-gap topological-insulator class with a single Dirac cone on the surface. Nature Phys. 5, 398–402 (2009).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nature Phys. 5, 438–442 (2009). References 12 and 13 report experiments and theory on next-generation topological insulator materials, which have a large bandgap and a single surface Dirac cone; these are the most promising materials for future experiments.
Chen, Y. L. et al. Experimental realization of a three-dimensional topological insulator, Bi2Te3 . Science 325, 178–181 (2009).
Castro Neto, A. H., Guinea, F., Peres, N. M., Novoselov, K. S. & Geim, A. K. The electronic properties of graphene. Rev. Mod. Phys. 81, 109–163 (2009).
Roushan, P. et al. Topological surface states protected from backscattering by chiral spin texture. Nature 460, 1106–1109 (2009).
Alpichshev, Z. et al. STM imaging of electronic waves on the surface of Bi2Te3: topologically protected surface states and hexagonal warping effects. Preprint at <http://arxiv.org/abs/0908.0371> (2009).
Zhang, T. et al. Experimental demonstration of the topological surface states protected by the time-reversal symmetry. Preprint at <http://arxiv.org/abs/0908.4136> (2009).
Nomura, K., Koshino, M. & Ryu, S. Topological delocalization of two-dimensional massless Dirac fermions. Phys. Rev. Lett. 99, 146806 (2007).
Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492–1505 (1958).
Li, J. et al. Topological Anderson insulator. Phys. Rev. Lett. 102, 136806 (2009).
Groth, C. W. et al. Theory of the topological Anderson insulator. Phys. Rev. Lett. 103, 196805 (2009).
Hsieh, D. et al. A tunable topological insulator in the spin helical Dirac transport regime. Nature 460, 1101–1105 (2009).
Seradjeh, B., Moore, J. E. & Franz, M. Exciton condensation and charge fractionalization in a topological insulator film. Phys. Rev. Lett. 103, 066402 (2009).
Peng, H. et al. Aharonov–Bohm interference in topological insulator nanoribbons. Preprint at <http://arxiv.org/abs/0908.3314> (2009).
Zhang, Y. et al. Crossover of three-dimensional topological insulator of Bi2Se3 to the two-dimensional limit. Preprint at <http://arxiv.org/abs/0911.3706> (2009).
Garate, I. & Franz, M. Inverse spin-galvanic effect in a topological-insulator/ferromagnet interface. Preprint at <http://arxiv.org/abs/0911.0106> (2009).
Wilczek, F. Two applications of axion electrodynamics. Phys. Rev. Lett. 58, 1799–1802 (1987).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Qi, X.-L. et al. Inducing a magnetic monopole with topological surface states. Science 323, 1184–1187 (2009).
Essin, A. M., Moore, J. E. & Vanderbilt, D. Magnetoelectric polarizability and axion electrodynamics in crystalline insulators. Phys. Rev. Lett. 102, 146805 (2009).
Ramesh, R. & Spaldin, N. A. Multiferroics: progress and prospects. Nature Mater. 6, 21–27 (2007).
Schnyder, A. P. et al. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Kitaev, A. Periodic table for topological insulators and superconductors. Preprint at <http://arxiv.org/abs/0901.2686> (2009).
Moore, J. E., Ran, Y. & Wen, X.-G. Topological surface states in three-dimensional magnetic insulators. Phys. Rev. Lett. 101, 186805 (2008).
Fu, L. & Kane, C. L. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys. Rev. Lett. 100, 096407 (2008).
Jackiw, R. & Rossi, P. Zero modes of the vortex-fermion system. Nucl. Phys. B 190, 681–691 (1980).
Wilczek, F. Majorana returns. Nature Physics 5, 614–618 (2009).
Nilsson, J., Akhmerov, A. R. & Beenakker, C. W. Splitting of a Cooper pair by a pair of Majorana bound states. Phys. Rev. Lett. 101, 120403 (2008).
Collins, G. P. Computing with quantum knots. Sci. Am. 294, 57–63 (2006).
Teo, J. & Kane, C. L. Majorana fermions and non-Abelian statistics in three dimensions. Phys. Rev. Lett. 104, 046401 (2009).
Acknowledgements
I have benefited from conversations about topological insulators with L. Balents, B. A. Bernevig, A. Essin, M. Franz, D. Haldane, Z. Hasan, C. Kane, D.-H. Lee, A. Ludwig, L. Molenkamp, S. Ryu, D. Vanderbilt, A. Vishwanath, X.-G. Wen, C. Xu and S.-C. Zhang. My work on topological insulators is supported by the US National Science Foundation.
Author information
Authors and Affiliations
Ethics declarations
Competing interests
The author declares no competing financial interest
Additional information
Reprints and permissions information is available at http://www.nature.com/reprints. Correspondence should be addressed to the author (jemoore@berkeley.edu).
Rights and permissions
About this article
Cite this article
Moore, J. The birth of topological insulators. Nature 464, 194–198 (2010). https://doi.org/10.1038/nature08916
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature08916
This article is cited by
-
Phase Relations in the Tl2Te-TlBiTe2-TlGdTe2 Compositions Region of the Tl-Bi-Gd-Te System and Magnetic Properties of the TlBi1−xGdxTe2 Solid Solutions
Journal of Phase Equilibria and Diffusion (2024)
-
Topology optimization of acoustic bandgap crystals for topological insulators
Engineering with Computers (2024)
-
Mixed state behavior of Hermitian and non-Hermitian topological models with extended couplings
Scientific Reports (2023)
-
Single-particle properties of topological Wannier excitons in bismuth chalcogenide nanosheets
Scientific Reports (2023)
-
Rigorous analysis of the topologically protected edge states in the quantum spin Hall phase of the armchair ribbon geometry
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.