Abstract
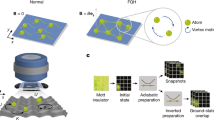
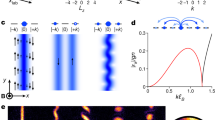
Neutral atomic Bose condensates and degenerate Fermi gases have been used to realize important many-body phenomena in their most simple and essential forms1,2,3, without many of the complexities usually associated with material systems. However, the charge neutrality of these systems presents an apparent limitation—a wide range of intriguing phenomena arise from the Lorentz force for charged particles in a magnetic field, such as the fractional quantum Hall effect in two-dimensional electron systems4,5. The limitation can be circumvented by exploiting the equivalence of the Lorentz force and the Coriolis force to create synthetic magnetic fields in rotating neutral systems. This was demonstrated by the appearance of quantized vortices in pioneering experiments6,7,8,9 on rotating quantum gases, a hallmark of superfluids or superconductors in a magnetic field. However, because of technical issues limiting the maximum rotation velocity, the metastable nature of the rotating state and the difficulty of applying stable rotating optical lattices, rotational approaches are not able to reach the large fields required for quantum Hall physics10,11,12. Here we experimentally realize an optically synthesized magnetic field for ultracold neutral atoms, which is evident from the appearance of vortices in our Bose–Einstein condensate. Our approach uses a spatially dependent optical coupling between internal states of the atoms, yielding a Berry’s phase13 sufficient to create large synthetic magnetic fields, and is not subject to the limitations of rotating systems. With a suitable lattice configuration, it should be possible to reach the quantum Hall regime, potentially enabling studies of topological quantum computation.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Greiner, M., Mandel, O., Esslinger, T., Hänsch, T. W. & Bloch, I. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms. Nature 415, 39–44 (2003)
Regal, C. A., Greiner, M. & Jin, D. S. Observation of resonance condensation of fermionic atom pairs. Phys. Rev. Lett. 92, 040403 (2004)
Zwierlein, M. W. et al. Condensation of pairs of fermionic atoms near a Feshbach resonance. Phys. Rev. Lett. 92, 120403 (2004)
Tsui, D. C., Stormer, H. L. & Gossard, A. C. Two-dimensional magnetotransport in the extreme quantum limit. Phys. Rev. Lett. 48, 1559–1562 (1982)
Laughlin, R. B. Anomalous quantum Hall effect: an incompressible quantum fluid with fractionally charged excitations. Phys. Rev. Lett. 50, 1395–1398 (1983)
Zwierlein, M. W., Abo-Shaeer, J. R., Schirotzek, A., Schunck, C. H. & Ketterle, W. Vortices and superfluidity in a strongly interacting Fermi gas. Nature 435, 1047–1051 (2005)
Schweikhard, V., Coddington, I., Engels, P., Mogendorff, V. P. & Cornell, E. A. Rapidly rotating Bose-Einstein condensates in and near the lowest Landau level. Phys. Rev. Lett. 92, 040404 (2004)
Madison, K. W., Chevy, F., Wohlleben, W. & Dalibard, J. Vortex formation in a stirred Bose-Einstein condensate. Phys. Rev. Lett. 84, 806–809 (2000)
Abo-Shaeer, J. R., Raman, C., Vogels, J. M. & Ketterle, W. Observation of vortex lattices in Bose-Einstein condensates. Science 292, 476–479 (2001)
Juzeliūnas, G. & Öhberg, P. Slow light in degenerate Fermi gases. Phys. Rev. Lett. 93, 033602 (2004)
Jaksch, D. & Zoller, P. Creation of effective magnetic fields in optical lattices: the Hofstadter butterfly for cold neutral atoms. N. J. Phys. 5, 56.1–56.11 (2003)
Sorensen, A. S., Demler, E. & Lukin, M. D. Fractional quantum Hall states of atoms in optical lattices. Phys. Rev. Lett. 94, 086803 (2005)
Berry, M. V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984)
Juzeliūnas, G., Ruseckas, J., Öhberg, P. & Fleischhauer, M. Light-induced effective magnetic fields for ultracold atoms in planar geometries. Phys. Rev. A 73, 025602 (2006)
Gunter, K. J., Cheneau, M., Yefsah, T., Rath, S. P. & Dalibard, J. Practical scheme for a light-induced gauge field in an atomic Bose gas. Phys. Rev. A 79, 011604 (2009)
Spielman, I. B. Raman processes and effective gauge potentials. Phys. Rev. A 79, 063613 (2009)
Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Sarma, S. D. Non-abelian anyons and topological quantum computation. Rev. Mod. Phys. 80, 1083–1159 (2008)
Radu, I. P. et al. Quasi-particle properties from tunneling in the formula fractional quantum Hall state. Science 320, 899–902 (2008)
Cooper, N. R. Rapidly rotating atomic gases. Adv. Phys. 57, 539–616 (2008)
Cheneau, M. et al. Geometric potentials in quantum optics: A semi-classical interpretation. Europhys Lett. 83, 60001 (2008)
Leanhardt, A. E. et al. Imprinting vortices in a Bose-Einstein condensate using topological phases. Phys. Rev. Lett. 89, 190403 (2002)
Andersen, M. F. et al. Quantized rotation of atoms from photons with orbital angular momentum. Phys. Rev. Lett. 97, 170406 (2006)
Matthews, M. R. et al. Vortices in a Bose-Einstein condensate. Phys. Rev. Lett. 83, 2498–2501 (1999)
Lin, Y.-J. et al. Bose-Einstein condensate in a uniform light-induced vector potential. Phys. Rev. Lett. 102, 130401 (2009)
Yarmchuk, E. J., Gordon, M. J. V. & Packard, R. E. Observation of stationary vortex arrays in rotating superfluid helium. Phys. Rev. Lett. 43, 214–217 (1979)
Lundh, E., Pethick, C. J. & Smith, H. Zero-temperature properties of a trapped Bose-condensed gas: beyond the Thomas-Fermi approximation. Phys. Rev. A 55, 2126–2131 (1997)
Murray, D. R., Öhberg, P., Gomila, D. & Barnett, S. M. Vortex nucleation in Bose-Einstein condensates due to effective magnetic fields. Phys. Rev. A 79, 063618 (2009)
Hofstadter, D. R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 14, 2239–2249 (1976)
Lin, Y.-J., Perry, A. R., Compton, R. L., Spielman, I. B. & Porto, J. V. Rapid production of 87 Rb Bose-Einstein condensates in a combined magnetic and optical potential. Phys. Rev. A 79, 063631 (2009)
Blakie, P. B., Bradley, A. S., Davis, M. J., Ballagh, R. J. & Gardiner, C. W. Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques. Adv. Phys. 57, 363–455 (2008)
Acknowledgements
We thank W. D. Phillips for discussions. This work was partially supported by ONR, ARO with funds from the DARPA OLE programme, and the NSF through the JQI Physics Frontier Center. R.L.C. acknowledges the NIST/NRC postdoctoral programme and K.J.-G. thanks CONACYT.
Author Contributions All authors contributed to writing of the manuscript. Y.-J.L. led the data collection effort (with assistance from R.L.C. and K.J.-G.). I.B.S. and J.V.P. designed the original apparatus, which was largely constructed by I.B.S., and Y.-J.L. implemented the specific changes required for the present experiment. I.B.S. conceived the experiment and performed numerical and analytic calculations. This work was supervised by I.B.S. with consultations from J.V.P.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Lin, YJ., Compton, R., Jiménez-García, K. et al. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009). https://doi.org/10.1038/nature08609
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature08609
This article is cited by
-
Three-dimensional solitons in Rydberg-dressed cold atomic gases with spin–orbit coupling
Scientific Reports (2023)
-
Observation of frustrated chiral dynamics in an interacting triangular flux ladder
Nature Communications (2023)
-
Realization of a fractional quantum Hall state with ultracold atoms
Nature (2023)
-
Controllable tunability of a Chern number within the electronic-nuclear spin system in diamond
npj Quantum Information (2023)
-
A novel method to realize quantum spin-phonon Hall insulator in a one-dimensional superconducting resonator lattice
Quantum Information Processing (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.