Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

Formation of evenly spaced ridges and valleys

Nature volume 460, pages 502–505 (2009)Cite this article

Abstract

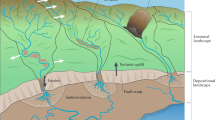
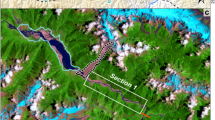
One of the most striking examples of self-organization in landscapes is the emergence of evenly spaced ridges and valleys1,2,3,4,5,6. Despite the prevalence of uniform valley spacing, no theory has been shown to predict this fundamental topographic wavelength. Models of long-term landscape evolution can produce landforms that look realistic7,8,9, but few metrics exist to assess the similarity between models and natural landscapes. Here we show that the ridge–valley wavelength can be predicted from erosional mechanics. From equations of mass conservation and sediment transport, we derive a characteristic length scale at which the timescales for erosion by diffusive soil creep and advective stream incision are equal. This length scale is directly proportional to the valley spacing that emerges in a numerical model of landform evolution, and to the measured valley spacing at five field sites. Our results provide a quantitative explanation for one of the most widely observed characteristics of landscapes. The findings also imply that valley spacing is a fundamental topographic signature that records how material properties and climate regulate erosional processes.

This is a preview of subscription content, access via your institution

Relevant articles

Open Access articles citing this article.

Access options

Rent or buy this article

Get just this article for as long as you need it

$39.95

Learn more

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Uniform valley spacing.
Figure 2: Comparison of predicted and observed valley spacing.
Figure 3: Measurement of model parameters from topography.

References

  1. Shaler, N. S. Spacing of rivers with reference to the hypothesis of base-levelling. Geol. Soc. Am. Bull. 10, 263–276 (1899)

    Article  ADS  Google Scholar 

  2. Izumi, N. & Parker, G. Inception of channelization and drainage basin formation: upstream-driven theory. J. Fluid Mech. 283, 341–363 (1995)

    Article  ADS  MathSciNet  Google Scholar 

  3. Hovius, N. Regular spacing of drainage outlets from linear mountain belts. Basin Res. 8, 29–44 (1996)

    Article  ADS  Google Scholar 

  4. Talling, P. J., Stewart, M. D., Stark, C. P., Gupta, S. & Vincent, S. J. Regular spacing of drainage outlets from linear fault blocks. Basin Res. 9, 275–302 (1997)

    Article  ADS  Google Scholar 

  5. Izumi, N. & Parker, G. Linear stability analysis of channel inception: downstream-driven theory. J. Fluid Mech. 419, 239–262 (2000)

    Article  ADS  MathSciNet  CAS  Google Scholar 

  6. Perron, J. T., Kirchner, J. W. & Dietrich, W. E. Spectral signatures of characteristic spatial scales and non-fractal structure in landscapes. J. Geophys. Res. 113 F04003 10.1029/2007JF000866 (2008)

    Article  ADS  Google Scholar 

  7. Willgoose, G., Bras, R. L. & Rodriguez-Iturbe, I. Results from a new model of river basin evolution. Earth Surf. Process. Landf. 16, 237–254 (1991)

    Article  ADS  Google Scholar 

  8. Howard, A. D. A detachment-limited model of drainage basin evolution. Wat. Resour. Res. 30, 2261–2286 (1994)

    Article  ADS  Google Scholar 

  9. Tucker, G. E. & Bras, R. L. Hillslope processes, drainage density, and landscape morphology. Wat. Resour. Res. 34, 2751–2764 (1998)

    Article  ADS  Google Scholar 

  10. Gilbert, G. K. Report on the Geology of the Henry Mountains 99–150 (US Government Printing Office, 1877)

    Google Scholar 

  11. Davis, W. M. The convex profile of badland divides. Science 20, 245 (1892)

    Article  ADS  CAS  Google Scholar 

  12. Gilbert, G. K. The convexity of hilltops. J. Geol. 17, 344–350 (1909)

    Article  ADS  Google Scholar 

  13. Smith, T. R. & Bretherton, F. P. Stability and the conservation of mass in drainage basin evolution. Wat. Resour. Res. 8, 1506–1529 (1972)

    Article  ADS  Google Scholar 

  14. Loewenherz, D. S. Stability and the initiation of channelized surface drainage: a reassessment of the short wavelength limit. J. Geophys. Res. 96, 8453–8464 (1991)

    Article  ADS  Google Scholar 

  15. Simpson, G. & Schlunegger, F. Topographic evolution and morphology of surfaces evolving in response to coupled fluvial and hillslope sediment transport. J. Geophys. Res. 108 2300 10.1029/2002JB002162 (2003)

    Article  ADS  Google Scholar 

  16. Dunne, T. Formation and controls of channel networks. Prog. Phys. Geogr. 4, 211–239 (1980)

    Article  Google Scholar 

  17. Kirkby, M. J. in Geomorphological Models: Theoretical and Empirical Aspects (ed. F. Ahnert) 1–14 (Catena, 1987)

    Google Scholar 

  18. Willgoose, G., Bras, R. L. & Rodriguez-Iturbe, I. A physical explanation of an observed link area-slope relationship. Wat. Resour. Res. 27, 1697–1702 (1991)

    Article  ADS  Google Scholar 

  19. Tarboton, D. G., Bras, R. L. & Rodriguez-Iturbe, I. A physical basis for drainage density. Geomorphology 5, 59–76 (1992)

    Article  ADS  Google Scholar 

  20. Howard, A. D. Badland morphology and evolution: Interpretation using a simulation model. Earth Surf. Process. Landf. 22, 211–227 (1997)

    Article  ADS  Google Scholar 

  21. Moglen, G. E., Eltahir, E. A. B. & Bras, R. L. On the sensitivity of drainage density to climate change. Wat. Resour. Res. 34, 855–862 (1998)

    Article  ADS  Google Scholar 

  22. Horton, R. E. Erosional development of streams and their drainage basins: hydrophysical approach to quantitative morphology. Bull. Geol. Soc. Am. 56, 275–370 (1945)

    Article  Google Scholar 

  23. Perron, J. T., Dietrich, W. E. & Kirchner, J. W. Controls on the spacing of first-order valleys. J. Geophys. Res. 113 F04016 10.1029/2007JF000977 (2008)

    Article  ADS  Google Scholar 

  24. Hilley, G. E. & Arrowsmith, J. R. Geomorphic response to uplift along the Dragon's Back pressure ridge, Carrizo Plain, California. Geology 36, 367–370 (2008)

    Article  ADS  Google Scholar 

  25. Fernandes, N. F. & Dietrich, W. E. Hillslope evolution by diffusive processes: the timescale for equilibrium adjustments. Wat. Resour. Res. 33, 1307–1318 (1997)

    Article  ADS  Google Scholar 

  26. Prosser, I. P. & Dietrich, W. E. Field experiments on erosion by overland flow and their implication for a digital terrain model of channel initiation. Wat. Resour. Res. 31, 2867–2876 (1995)

    Article  ADS  Google Scholar 

  27. Montgomery, D. R. & Dietrich, W. E. Where do channels begin? Nature 336, 232–234 (1988)

    Article  ADS  Google Scholar 

  28. Montgomery, D. R. & Dietrich, W. E. Channel initiation and the problem of landscape scale. Science 255, 826–830 (1992)

    Article  ADS  CAS  Google Scholar 

  29. Rinaldo, A., Dietrich, W. E., Rigon, R., Vogel, G. K. & Rodriguez-Iturbe, I. Geomorphological signatures of varying climate. Nature 374, 632–635 (1995)

    Article  ADS  CAS  Google Scholar 

  30. Seidl, M. A. & Dietrich, W. E. in Functional Geomorphology (eds K. H. Schmidt & J. de Ploey) 101–124 (Catena, 1992)

    Google Scholar 

Download references

Acknowledgements

This work was supported by the National Science Foundation (J.T.P.), the Institute for Geophysics and Planetary Physics (J.W.K. and J.T.P.), and NASA (W.E.D. and J.T.P.). Laser altimetry for Gabilan Mesa was acquired and processed by NCALM (http://www.ncalm.org) with support from the National Center for Earth-surface Dynamics (NCED). We thank the Orradre family of San Ardo, California, for granting access to their land. We thank the states of Pennsylvania and Utah for making laser altimetry data publicly available. We also thank K. Whipple for his review.

Author information

Authors and Affiliations

  1. Department of Earth, Atmospheric and Planetary Sciences, Massachusetts Institute of Technology, Cambridge, Massachusetts 02139, USA,

    J. Taylor Perron

  2. Department of Earth and Planetary Science, University of California, Berkeley, California 94720, USA,

    James W. Kirchner & William E. Dietrich

  3. Swiss Federal Institute for Forest, Snow and Landscape Research (WSL), Birmensdorf, Switzerland

    James W. Kirchner

  4. Department of Environmental Sciences, Swiss Federal Institute of Technology (ETH), Zürich, Switzerland

    James W. Kirchner

Authors
  1. J. Taylor Perron
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. James W. Kirchner
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. William E. Dietrich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to J. Taylor Perron.

Supplementary information

Supplementary Information

This file contains Supplementary Methods, Supplementary Figures S1-S3 with Legends, Supplementary Table S1 and Supplementary References. (PDF 1107 kb)

Supplementary Movie 1

This movie shows the evolution of the model landscape over 600 kyr. Competition for drainage area (a proxy for water flux) among the irregularly spaced, incipient valleys that arise in the random initial surface eventually leads to an equilibrium landscape with evenly spaced valleys. Horizontal tick interval is 200 m, vertical tick interval is 20 m. (MP4 2177 kb)

PowerPoint slides

Rights and permissions

Reprints and Permissions

About this article

Cite this article

Perron, J., Kirchner, J. & Dietrich, W. Formation of evenly spaced ridges and valleys. Nature 460, 502–505 (2009). https://doi.org/10.1038/nature08174

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature08174

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing