Abstract
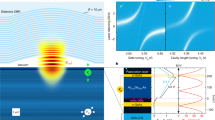
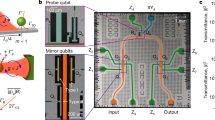
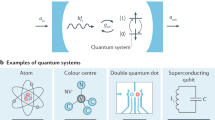
The field of cavity quantum electrodynamics (QED), traditionally studied in atomic systems1,2,3, has gained new momentum by recent reports of quantum optical experiments with solid-state semiconducting4,5,6,7,8 and superconducting9,10,11 systems. In cavity QED, the observation of the vacuum Rabi mode splitting is used to investigate the nature of matter–light interaction at a quantum-mechanical level. However, this effect can, at least in principle, be explained classically as the normal mode splitting of two coupled linear oscillators12. It has been suggested that an observation of the scaling of the resonant atom–photon coupling strength in the Jaynes–Cummings energy ladder13 with the square root of photon number n is sufficient to prove that the system is quantum mechanical in nature14. Here we report a direct spectroscopic observation of this characteristic quantum nonlinearity. Measuring the photonic degree of freedom of the coupled system, our measurements provide unambiguous spectroscopic evidence for the quantum nature of the resonant atom–field interaction in cavity QED. We explore atom–photon superposition states involving up to two photons, using a spectroscopic pump and probe technique. The experiments have been performed in a circuit QED set-up15, in which very strong coupling is realized by the large dipole coupling strength and the long coherence time of a superconducting qubit embedded in a high-quality on-chip microwave cavity. Circuit QED systems also provide a natural quantum interface between flying qubits (photons) and stationary qubits for applications in quantum information processing and communication16.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout





Similar content being viewed by others
References
Raimond, J. M., Brune, M. & Haroche, S. Manipulating quantum entanglement with atoms and photons in a cavity. Rev. Mod. Phys. 73, 565–582 (2001)
Mabuchi, H. & Doherty, A. C. Cavity quantum electrodynamics: Coherence in context. Science 298, 1372–1377 (2002)
Walther, H., Varcoe, B. T. H., Englert, B.-G. & Becker, T. Cavity quantum electrodynamics. Rep. Prog. Phys. 69, 1325–1382 (2006)
Reithmaier, J. P. et al. Strong coupling in a single quantum dot-semiconductor microcavity system. Nature 432, 197–200 (2004)
Yoshie, T. et al. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 432, 200–203 (2004)
Peter, E. et al. Exciton-photon strong-coupling regime for a single quantum dot embedded in a microcavity. Phys. Rev. Lett. 95, 067401 (2005)
Hennessy, K. et al. Quantum nature of a strongly coupled single quantum dot-cavity system. Nature 445, 896–899 (2007)
Englund, D. et al. Controlling cavity reflectivity with a single quantum dot. Nature 450, 857–861 (2007)
Wallraff, A. et al. Strong coupling of a single photon to a superconducting qubit using circuit quantum electrodynamics. Nature 431, 162–167 (2004)
Chiorescu, I. et al. Coherent dynamics of a flux qubit coupled to a harmonic oscillator. Nature 431, 159–162 (2004)
Johansson, J. et al. Vacuum Rabi oscillations in a macroscopic superconducting qubit LC oscillator system. Phys. Rev. Lett. 96, 127006 (2006)
Zhu, Y. et al. Vacuum Rabi splitting as a feature of linear-dispersion theory: Analysis and experimental observations. Phys. Rev. Lett. 64, 2499–2502 (1990)
Walls, D. & Milburn, G. Quantum Optics (Springer, Berlin, 1994)
Carmichael, H. J., Kochan, P. & Sanders, B. C. Photon correlation spectroscopy. Phys. Rev. Lett. 77, 631–634 (1996)
Blais, A., Huang, R. S., Wallraff, A., Girvin, S. M. & Schoelkopf, R. J. Cavity quantum electrodynamics for superconducting electrical circuits: An architecture for quantum computation. Phys. Rev. A 69, 062320 (2004)
Nielsen, M. A. & Chuang, I. L. Quantum Computation and Quantum Information (Cambridge Univ. Press, Cambridge, UK, 2000)
Thompson, R. J., Rempe, G. & Kimble, H. J. Observation of normal-mode splitting for an atom in an optical cavity. Phys. Rev. Lett. 68, 1132–1135 (1992)
Boca, A. et al. Observation of the vacuum Rabi spectrum for one trapped atom. Phys. Rev. Lett. 93, 233603 (2004)
Brune, M. et al. Quantum Rabi oscillation: A direct test of field quantization in a cavity. Phys. Rev. Lett. 76, 1800–1803 (1996)
Varcoe, B. T. H., Brattke, S., Weidinger, M. & Walther, H. Preparing pure photon number states of the radiation field. Nature 403, 743–746 (2000)
Bertet, P. et al. Generating and probing a two-photon Fock state with a single atom in a cavity. Phys. Rev. Lett. 88, 143601 (2002)
Thompson, R. J., Turchette, Q. A., Carnal, O. & Kimble, H. J. Nonlinear spectroscopy in the strong-coupling regime of cavity QED. Phys. Rev. A 57, 3084–3104 (1998)
Schuster, D. I. et al. Resolving photon number states in a superconducting circuit. Nature 445, 515–518 (2007)
Guerlin, C. et al. Progressive field-state collapse and quantum non-demolition photon counting. Nature 448, 889–893 (2007)
Koch, J. et al. Charge-insensitive qubit design derived from the Cooper pair box. Phys. Rev. A 76, 042319 (2007)
Schreier, J. A. et al. Suppressing charge noise decoherence in superconducting charge qubits. Phys. Rev. B 77, 180502(R) (2008)
Bouchiat, V., Vion, D., Joyez, P., Esteve, D. & Devoret, M. H. Quantum coherence with a single Cooper pair. Phys. Scripta T76, 165–170 (1998)
Schuster, D. I. et al. AC Stark shift and dephasing of a superconducting qubit strongly coupled to a cavity field. Phys. Rev. Lett. 94, 123602 (2005)
Schoelkopf, R. J. & Girvin, S. M. Wiring up quantum systems. Nature 451, 664–669 (2008)
Schuster, I. et al. Nonlinear spectroscopy of photons bound to one atom. Nature Phys. 4, 382–385 (2008)
Acknowledgements
We thank L. S. Bishop, J. M. Chow, T. Esslinger, L. Frunzio, A. Imamoğlu, B. R. Johnson, J. Koch, R. J. Schoelkopf and D. I. Schuster for discussions. This work was supported by SNF and ETHZ. P.J.L. was supported by the EU with an MC-EIF. A.B. was supported by NSERC, CIFAR and FQRNT.
Author Contributions J.M.F. performed the experiments and analysed the data using theory developed by A.B.; M.G. designed and fabricated the sample; M.B. contributed to sample characterization; R.B. contributed to the realization of the experimental set-up; and J.M.F. and A.W. co-wrote the paper. All authors discussed the results and commented on the manuscript. P.J.L. and A.W. supervised this work.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
About this article
Cite this article
Fink, J., Göppl, M., Baur, M. et al. Climbing the Jaynes–Cummings ladder and observing its nonlinearity in a cavity QED system. Nature 454, 315–318 (2008). https://doi.org/10.1038/nature07112
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature07112
This article is cited by
-
An ultra-high gain single-photon transistor in the microwave regime
Nature Communications (2022)
-
Lamb shift statistics in mesoscopic quantum ensembles
Quantum Information Processing (2022)
-
Dynamics of atomic magic in the Jaynes–Cummings model
Quantum Information Processing (2022)
-
Quantum information processing and quantum optics with circuit quantum electrodynamics
Nature Physics (2020)
-
Demystifying the spectral collapse in two-photon Rabi model
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.