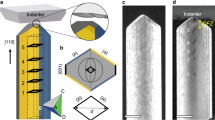
Abstract
The formation of dislocations is central to our understanding of yield, work hardening, fracture, and fatigue1 of crystalline materials. While dislocations have been studied extensively in conventional materials, recent results have shown that colloidal crystals offer a potential model system for visualizing their structure and dynamics directly in real space2. Although thermal fluctuations are thought to play a critical role in the nucleation of these defects, it is difficult to observe them directly. Nano-indentation, during which a small tip deforms a crystalline film, is a common tool for introducing dislocations into a small volume that is initially defect-free3,4,5,6,7,8,9,10. Here, we show that an analogue of nano-indentation performed on a colloidal crystal provides direct images of defect formation in real time and on the single particle level, allowing us to probe the effects of thermal fluctuations. We implement a new method to determine the strain tensor of a distorted crystal lattice and we measure the critical dislocation loop size and the rate of dislocation nucleation directly. Using continuum models, we elucidate the relation between thermal fluctuations and the applied strain that governs defect nucleation. Moreover, we estimate that although bond energies between particles are about fifty times larger in atomic systems, the difference in attempt frequencies makes the effects of thermal fluctuations remarkably similar, so that our results are also relevant for atomic crystals.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout




Similar content being viewed by others
References
Hirth, J. P. & Lothe, J. Theory of Dislocations Edn 2 (Wiley, New York, 1982)
Schall, P., Cohen, I., Weitz, D. A. & Spaepen, F. Visualization of dislocation dynamics in collidal crystals. Science 305, 1944–1948 (2004)
Suresh, S., Nieh, T.-G. & Choi, B. W. Nano-indentation of copper thin films on silicon substrates. Scr. Mater. 41, 951–957 (1999)
Kiely, J. D., Jarausch, K. F., Houston, J. E. & Russell, P. E. Initial stages of yield in nanoindentation. J. Mater. Res. 14, 2219–2227 (1999)
Li, J., van Vliet, K. J., Zhu, T., Yip, S. & Suresh, S. Atomistic mechanism governing elastic limit and incipient plasticity in crystals. Nature 418, 307–310 (2002)
Gouldstone, A., Van Vliet, K. J. & Suresh, S. Simulation of defect nucleation in a crystal. Nature 411, 656 (2001)
Kelchner, C. L., Plimpton, S. J. & Hamilton, J. C. Dislocation nucleation and defect structure during surface indentation. Phys. Rev. B 58, 11085–11088 (1998)
Lilleodden, E. T., Zimmerman, J. A., Foiles, S. M. & Nix, W. D. Atomistic simulations of elastic deformation and dislocation nucleation during nanoindentation. J. Mech. Phys. Sol. 51, 901–920 (2003)
Stach, E. A. et al. Development of a nanoindenter for in situ transmission electron micoroscopy. Microsc. Microanal. 7, 507–517 (2001)
Minor, A. M., Lilleodden, E. T., Stach, E. A. & Morris, J. W. Direct observation of incipient plasticity during nanoindentation of Al. J. Mater. Res. 19, 176–182 (2004)
van Blaaderen, A., Ruel, R. & Wiltzius, P. Template-directed colloidal crystallization. Nature 385, 321–324 (1997)
Weeks, E. R., Crocker, J. C., Levitt, A. C., Schofield, A. & Weitz, D. A. Three-dimensional direct space imaging of structural relaxation near the colloidal glass transition. Science 287, 627–631 (2000)
Falk, M. L. & Langer, J. S. Dynamics of viscoplastic deformation in amorphous solids. Phys. Rev. E 57, 7192–7205 (1998)
Frank, F. C. in Symposium on Plastic Deformation of Crystalline Solids 89–102 (Carnegie Institute of Technology and Office of Naval Research, Pittsburgh, 1950)
Hirth, J. P. in The Relation Between the Structure and the Mechanical Properties of Metals 217–228 (Her Majesty's Stationery Office, London, 1963)
Cottrell, A. H. Dislocations and Plastic Flow in Crystals (Oxford Univ. Press, Oxford, 1956)
Davies, R. M. The determination of static and dynamic yield stresses using a steel ball. Proc. R. Soc. Lond. A 197, 416–432 (1949)
Chaikin, P. M. & Lubensky, T. C. Principles of Condensed Matter Physics Ch. 7.4.5 (Cambridge Univ. Press, Cambridge, 1995)
Higashigaki, Y., Christensen, D. H. & Wang, C. H. Studies of the reorientational motion and intermolecular interaction of dimethylsulfoxide in water by depolarized Rayleigh-scattering. J. Phys. Chem. 85, 2531–2535 (1981)
Frenkel, D. & Ladd, A. J. C. Elastic constants of hard-sphere crystals. Phys. Rev. Lett. 59, 1169 (1987)
Acknowledgements
We thank R. Christianson and D. Blair for their help with the image analysis, M.L. Falk for discussions about the strain algorithm, and D. Bonner for help with programming the strain algorithm. This work was supported by a Lynen Fellowship from the Alexander von Humboldt Foundation (P.S.), and by NSF and Harvard MRSEC grants.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
Reprints and permissions information is available at npg.nature.com/reprintsandpermissions. The authors declare no competing financial interests.
Supplementary information
Supplementary Video
This movie shows laser diffraction microscopy images of the nucleation and growth of dislocations during indentation of a colloidal crystalline film. The time lapse covers a period of 10 h, during which we slowly move the indenting tip into the crystalline sediment at a rate of 3.4µm/h and subsequently pull it back at a rate of 20µm/min. After the initial emergence of a strain field depicted as a two-armed contrast profile and the nucleation of a first dislocation loop depicted as a dark circular spot, a complex dislocation structure evolves. This structure relaxes and partially heals when the needle moves back up. These images also show local intensity fluctuations in both the strained and unstrained crystal lattice that correspond to thermally excited fluctuations in the particle configurations. (MOV 8836 kb)
Rights and permissions
About this article
Cite this article
Schall, P., Cohen, I., Weitz, D. et al. Visualizing dislocation nucleation by indenting colloidal crystals. Nature 440, 319–323 (2006). https://doi.org/10.1038/nature04557
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature04557
This article is cited by
-
Dislocation interactions during plastic relaxation of epitaxial colloidal crystals
Nature Communications (2023)
-
Visualizing defect dynamics by assembling the colloidal graphene lattice
Nature Communications (2023)
-
Macroscopic materials assembled from nanoparticle superlattices
Nature (2021)
-
Diffusive and martensitic nucleation kinetics in solid-solid transitions of colloidal crystals
Nature Communications (2017)
-
Diffusive, Displacive Deformations and Local Phase Transformation Govern the Mechanics of Layered Crystals: The Case Study of Tobermorite
Scientific Reports (2017)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.