Abstract
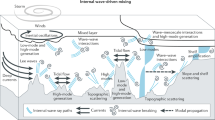
Ocean mixing, which affects pollutant dispersal, marine productivity and global climate1, largely results from the breaking of internal gravity waves—disturbances propagating along the ocean's internal stratification. A global map of internal-wave dissipation would be useful in improving climate models, but would require knowledge of the sources of internal gravity waves and their propagation. Towards this goal, I present here computations of horizontal internal-wave propagation from 60 historical moorings and relate them to the source terms of internal waves as computed previously2,3. Analysis of the two most energetic frequency ranges—near-inertial frequencies and semidiurnal tidal frequencies—reveals that the fluxes in both frequency bands are of the order of 1 kW m-1 (that is, 15–50% of the energy input) and are directed away from their respective source regions. However, the energy flux due to near-inertial waves is stronger in winter, whereas the tidal fluxes are uniform throughout the year. Both varieties of internal waves can thus significantly affect the space-time distribution of energy available for global mixing.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Gregg, M. Diapycnal mixing in the thermocline. J. Geophys. Res. 92, 5249–5286 (1987)
Egbert, G. D. & Ray, R. D. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature 405, 775–778 (2000)
Alford, M. H. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophys. Res. Lett. 30(8), doi:10.1029/2002GL016614 (2000)
Manabe, S. & Stouffer, R. J. Two stable equilibria of a coupled ocean-atmosphere model. J. Clim. 1, 841–866 (1988)
Munk, W. & Wunsch, C. Abyssal recipes II: energetics of tidal and wind mixing. Deep-Sea Res. I 45, 1977–2010 (1998)
Ganchaud, A. & Wunsch, C. Improved estimates of global ocean circulation, heat transport and mixing from hydrographic data. Nature 408, 453–456 (2000)
Webb, D. J. & Suginohara, N. Vertical mixing in the ocean. Nature 409, 37–39 (2001)
Wunsch, C. The work done by the wind on the oceanic general circulation. J. Phys. Oceanogr. 28, 2332–2340 (1998)
Alford, M. H. Internal swell generation: the spatial distribution of energy flux from the wind to mixed-layers near-inertial motions. J. Phys. Oceanogr. 31, 2359–2368 (2001)
Ledwell, J. R., Watson, A. J. & Law, C. S. Evidence for slow mixing across the pycnocline from an open-ocean tracer-release experiment. Nature 364, 701–703 (1993)
Polzin, K. L., Toole, J. M., Ledwell, G. R. & Schmitt, R. W. Spatial variability of turbulent mixing in the abyssal ocean. Science 276, 93–96 (1997)
Samelson, R. M. Large-scale circulation with locally enhanced vertical mixing. J. Phys. Oceanogr. 28, 712–726 (1998)
D'Asaro, E. The energy flux from the wind to near-inertial motions in the mixed layer. J. Phys. Oceanogr. 15, 943–959 (1985)
Gill, A. E. On the behavior of internal waves in the wake of a storm. J. Phys. Oceanogr. 14, 1129–1151 (1984)
D'Asaro, E. et al. Upper-ocean inertial currents forced by a storm, I, data and comparisons with linear theory. J. Phys. Oceanogr. 25, 2909–2936 (1995)
Alford, M. & Gregg, M. Near-inertial mixing: modulation of shear, strain and microstructure at low latitude. J. Geophys. Res. 106, 16947–16968 (2001)
Ray, R. D. & Mitchum, G. T. Surface manifestations of internal tides in the deep ocean: observations from altimetry and island gauges. Prog. Oceanogr. 40, 135–162 (1997)
Ray, R. D. & Cartwright, D. E. Estimates of internal tide energy fluxes from TOPEX/ POSEIDON altimetry: central North Pacific. Geophys. Res. Lett. 28, 1259–1262 (2001)
D'Asaro, E. A. in Proc. Dynamics of Oceanic Internal Gravity Waves II (eds Müller, P. & Henderson, D.) 451–466 (‘Aha Huliko'a Hawaiian Winter Workshop, Hawaii Institute of Geophysics, Honolulu, 1991)
Garrett, C. What is the “near-inertial” band and why is it different from the rest of the internal wave spectrum? J. Phys. Oceanogr. 31, 962–971 (2001)
Levitus, S. & Boyer, T. World Ocean Atlas 1994 (NOAA Atlas NESDIS 4, US Department of Commerce, Washington DC, 1994).
Thorpe, S. A. On internal wave groups. J. Phys. Oceanogr. 29, 1085–1095 (1999)
Pingree, R. D. & New, A. L. Abyssal penetration and bottom reflection of internal tidal energy in the Bay of Biscay. J. Phys. Oceanogr. 21, 28–39 (1991)
Dushaw, B., Cornuelle, B., Worcester, P. F., Howe, B. & Luther, D. Barotropic and baroclinic tides in the Central North Pacific Ocean determined from long-range reciprocal acoustic transmissions. J. Phys. Oceanogr. 25, 631–647 (1995)
Doherty, K. W., Frye, D. E., Liberatore, S. P. & Toole, J. M. A moored profiling instrument. J. Atmos. Ocean Technol. 16, 1816–1829 (1999)
St Laurent, L. & Garrett, C. The role of internal tides in mixing the deep ocean. J. Phys. Oceanogr. 32, 2882–2899 (2001)
Merrifield, M. A. & Holloway, P. E. Model estimates of M2 internal tide energetics at the Hawaiian Ridge. J. Geophys. Res. 107, doi:10.1029/2001JC000996 (2002)
Garrett, C. J. R. & Munk, W. H. Space-time scales of internal waves: a progress report. J. Geophys. Res. 80, 291–297 (1975)
Fu, L. L. Observations and models of inertial waves in the deep ocean. Rev. Geophys. Space Phys. 19, 141–170 (1981)
Kunze, E., Rosenfield, L., Carter, G. & Gregg, M. C. Internal waves in Monterey submarine canyon. J. Phys. Oceanogr. 32, 1890–1913 (2002)
Acknowledgements
I thank E. D'Asaro, E. Kunze and C. Garrett for insights and discussions, and M. Whitmont for quality control and preparation of the mooring data. This work was supported by the Office of Naval Research Young Investigator award.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Rights and permissions
About this article
Cite this article
Alford, M. Redistribution of energy available for ocean mixing by long-range propagation of internal waves. Nature 423, 159–162 (2003). https://doi.org/10.1038/nature01628
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature01628
This article is cited by
-
The effect of Typhoon Kalmaegi on the modal energy and period of internal waves near the Dongsha Islands (South China Sea)
Acta Oceanologica Sinica (2024)
-
Cross-shelf variation of internal tides west of the Dongsha Plateau in the northern South China Sea
Acta Oceanologica Sinica (2023)
-
Internal-Wave Convection and Shear Near the Top of a Deep Equatorial Seamount
Pure and Applied Geophysics (2023)
-
Impact of Different Wind Representations on Resonant Ocean Near-inertial Motions in the Gulf of Mexico
Ocean Science Journal (2022)
-
The near-inertial waves observed east of the Philippines
Journal of Oceanology and Limnology (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.