Abstract
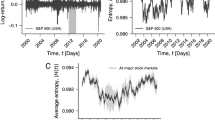
Insights into the dynamics of a complex system are often gained by focusing on large fluctuations. For the financial system, huge databases now exist that facilitate the analysis of large fluctuations and the characterization of their statistical behaviour1,2. Power laws appear to describe histograms of relevant financial fluctuations, such as fluctuations in stock price, trading volume and the number of trades3,4,5,6,7,8,9,10. Surprisingly, the exponents that characterize these power laws are similar for different types and sizes of markets, for different market trends and even for different countries—suggesting that a generic theoretical basis may underlie these phenomena. Here we propose a model, based on a plausible set of assumptions, which provides an explanation for these empirical power laws. Our model is based on the hypothesis that large movements in stock market activity arise from the trades of large participants. Starting from an empirical characterization of the size distribution of those large market participants (mutual funds), we show that the power laws observed in financial data arise when the trading behaviour is performed in an optimal way. Our model additionally explains certain striking empirical regularities that describe the relationship between large fluctuations in prices, trading volume and the number of trades.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Takayasu, H. (ed.) Empirical Science of Financial Fluctuations: The Advent of Econophysics (Springer, Berlin, 2002)
Bunde, A., Schellnhuber, H. J. & Kropp, J. (eds) The Science of Disasters: Climate Disruptions, Heart Attacks, and Market Crashes (Springer, Berlin, 2002)
Mandelbrot, B. B. The variation of certain speculative prices. J. Business 36, 394–419 (1963)
Lux, T. The stable Paretian hypothesis and the frequency of large returns: an examination of major German stocks. Appl. Fin. Econ. 6, 463–475 (1996)
Liu, Y. et al. The statistical properties of the volatility of price fluctuations. Phys. Rev. E 60, 1390–1400 (1999)
Guillaume, D. M. et al. From the bird's eye to the microscope: a survey of new stylized facts of the intra-daily foreign exchange markets. Fin. Stochastics 1, 95–129 (1997)
Plerou, V., Gopikrishnan, P., Amaral, L. A. N., Meyer, M. & Stanley, H. E. Scaling of the distribution of price fluctuations of individual companies. Phys. Rev. E 60, 6519–6529 (1999)
Gopikrishnan, P., Plerou, V., Amaral, L. A. N., Meyer, M. & Stanley, H. E. Scaling of the distributions of fluctuations of financial market indices. Phys. Rev. E 60, 5305–5316 (1999)
Gopikrishnan, P., Plerou, V., Gabaix, X. & Stanley, H. E. Statistical properties of share volume traded in financial markets. Phys. Rev. E 62, R4493–R4496 (2000)
Plerou, V., Gopikrishnan, P., Amaral, L. A. N., Gabaix, X. & Stanley, H. E. Economic fluctuations and anomalous diffusion. Phys. Rev. E 62, R3023–R3026 (2000)
Keim, D. & Madhavan, A. Transactions costs and investment style: An inter-exchange analysis of institutional equity trades. J. Fin. Econ. 46, 265–292 (1997)
Chan, L. & Lakonishok, J. The behavior of stock prices around institutional trades. J. Fin. 50, 1147–1174 (1995)
Wurgler, J. & Zhuravskaya, K. Does arbitrage flatten demand curves for stocks? J. Business 75, 583–608 (2002)
Bagwell, L. Dutch auction repurchases: An analysis of shareholder heterogeneity. J. Fin. 47, 71–105 (1992)
Kyle, A. S. Continuous auctions and insider trading. Econometrica 53, 1315–1335 (1985)
Grossman, S. & Miller, M. Liquidity and market structure. J. Fin. 43, 617–633 (1988)
O'Hara, M. Market Microstructure Theory (Blackwell, Oxford, 1997)
Cutler, D., Poterba, J. M. & Summers, L. H. What moves stock prices? J. Portfolio Management 15, 4–12 (1989)
Zipf, G. Human Behavior and the Principle of Least Effort (Addiston-Wesley, Cambridge, 1949)
Okuyama, K., Takayasu, M. & Takayasu, H. Zipf's law in income distribution of companies. Physica A 269, 125–131 (1999)
Axtell, R. Zipf distribution of U.S. firm sizes. Science 293, 1818–1820 (2001)
Gabaix, X. Zipf's law for cities: An explanation. Q. J. Econ. 114, 739–767 (1999)
Hasbrouck, J. Measuring the information content of stock trades. J. Fin. 46, 179–207 (1991)
Plerou, V., Gopikrishnan, P., Gabaix, X. & Stanley, H. E. Quantifying stock price response to demand fluctuations. Phys. Rev. E 66, 027104 (2002)
Daniel, K., Hirshleifer, D. & Subrahmanyam, A. Investor psychology and security market under- and over-reactions. J. Fin. 53, 1839–1885 (1998)
Shleifer, A. Inefficient Markets: An Introduction to Behavioral Finance (Oxford Univ Press, Oxford, 2000)
Gabaix, X., Ramalho, R. & Reuter, J. Power laws and mutual fund dynamics (MIT Mimeo, Massachusetts Institute of Technology, Cambridge, 2003)
Lee, C. M. C. & Ready, M. J. Inferring trade direction from intraday data. J. Fin. 46, 733–746 (1991)
Acknowledgements
We thank the National Science Foundation's economics program and the Russell Sage Foundation for support, K. Doran for research assistance, and M. Avellaneda, R. Barro, O. Blanchard, J. Campbell, A. Dixit, J. Hasbrouck, C. Hopman, D. Laibson, L. Pedersen, T. Philippon, R. Ramalho, J. Reuter, G. Saar, J. Scheinkman, A. Shleifer, D. Vayanos and J. Wang for discussions.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Supplementary information
Rights and permissions
About this article
Cite this article
Gabaix, X., Gopikrishnan, P., Plerou, V. et al. A theory of power-law distributions in financial market fluctuations. Nature 423, 267–270 (2003). https://doi.org/10.1038/nature01624
Received:
Accepted:
Issue Date:
DOI: https://doi.org/10.1038/nature01624
This article is cited by
-
Business cycle and herding behavior in stock returns: theory and evidence
Financial Innovation (2024)
-
Age and market capitalization drive large price variations of cryptocurrencies
Scientific Reports (2023)
-
Price Change and Trading Volume: Behavioral Heterogeneity in Stock Market
Computational Economics (2023)
-
Detecting the lead–lag effect in stock markets: definition, patterns, and investment strategies
Financial Innovation (2022)
-
Multifractal analysis of social media use in financial markets
Journal of the Korean Physical Society (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.