Abstract
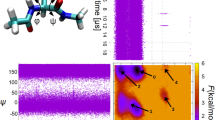
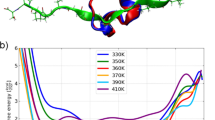
Protein folding is difficult to simulate with classical molecular dynamics. Secondary structure motifs such as α-helices and β-hairpins can form in 0.1–10 µs (ref. 1), whereas small proteins have been shown to fold completely in tens of microseconds2. The longest folding simulation to date is a single 1-µs simulation of the villin headpiece3; however, such single runs may miss many features of the folding process as it is a heterogeneous reaction involving an ensemble of transition states4,5. Here, we have used a distributed computing implementation to produce tens of thousands of 5–20-ns trajectories (700 µs) to simulate mutants of the designed mini-protein BBA5. The fast relaxation dynamics these predict were compared with the results of laser temperature-jump experiments. Our computational predictions are in excellent agreement with the experimentally determined mean folding times and equilibrium constants. The rapid folding of BBA5 is due to the swift formation of secondary structure. The convergence of experimentally and computationally accessible timescales will allow the comparison of absolute quantities characterizing in vitro and in silico (computed) protein folding6.
This is a preview of subscription content, access via your institution
Access options
Subscribe to this journal
Receive 51 print issues and online access
$199.00 per year
only $3.90 per issue
Buy this article
- Purchase on Springer Link
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout



Similar content being viewed by others
References
Eaton, W. A., Muñoz, V., Thompson, P. A., Henry, E. R. & Hofrichter, J. Kinetics and dynamics of loops, α-helices, β-hairpins, and fast-folding proteins. Acc. Chem. Res. 31, 745–753 (1998)
Mayor, U., Johnson, C. M., Daggett, V. & Fersht, A. R. Protein folding and unfolding in microseconds to nanoseconds by experiment and simulation. Proc. Natl Acad. Sci. USA 97, 13518–13522 (2000)
Duan, Y. & Kollman, P. A. Pathways to a protein folding intermediate observed in a 1-microsecond simulation in aqueous solution. Science 282, 740–744 (1998)
Wolynes, P. G., Onuchic, J. N. & Thirumalai, D. Navigating the folding routes. Science 267, 1619–1620 (1995)
Dill, K. A. & Chan, H. S. From Levinthal to pathways to funnels. Nature Struct. Biol. 4, 10–19 (1997)
Shea, J. & Brooks, C. L. From folding theories to folding proteins: a review and assessment of simulation studies of protein folding and unfolding. Annu. Rev. Phys. Chem. 52, 499–535 (2001)
Ferrara, P., Apostolakis, J. & Caflisch, A. Thermodynamics and kinetics of folding of two model peptides investigated by molecular dynamics simulations. J. Phys. Chem. B 104, 5000–5010 (2000)
Daura, X., Jaun, B., Seebach, D., Gunsteren, W. F. v. & Mark, A. E. Reversible peptide folding in solution by molecular dynamics simulation. J. Mol. Biol. 280, 925–932 (1998)
Ferrara, P. & Caflisch, A. Folding simulations of a three-stranded antiparallel β-sheet peptide. Proc. Natl Acad. Sci. USA 97, 10780–10785 (2000)
Zagrovic, B., Sorin, E. J. & Pande, V. S. β-hairpin folding simulations in atomistic detail using an implicit solvent model. J. Mol. Biol. 313, 151–169 (2001)
Fersht, A. R., Matouschek, A. & Serrano, L. The folding of an enzyme I. Theory of protein engineering analysis of stability and pathway of protein folding. J. Mol. Biol. 224, 771–782 (1992)
Lapidus, L. J., Eaton, W. A. & Hofrichter, J. Measuring the rate of intramolecular contact formation in polypeptides. Proc. Natl Acad. Sci. USA 97, 7220–7225 (2000)
Bieri, O. et al. The speed limit of protein folding measure by triplet-triplet energy transfer. Proc. Natl Acad. Sci. USA 96, 9597–9601 (1999)
Shirts, M. & Pande, V. S. Screen savers of the world unite. Science 290, 1903–1904 (2000)
Struthers, M., Ottesen, J. J. & Imperiali, B. Design and NMR analyses of compact, independently folded BBA motifs. Folding Des. 3, 95–103 (1998)
Struthers, M. D., Cheng, R. C. & Imperiali, B. Design of a monomeric 23-residue polypeptide with defined tertiary structure. Science 271, 342–345 (1996)
Ervin, J., Sabelko, J. & Gruebele, M. Submicrosecond real-time fluorescence detection: application to protein folding. J. Photochem. Photobiol. Biol. 54, 1–15 (2000)
Chandler, D. Statistical mechanics of isomerization dynamics in liquids and the transition state approximation. J. Chem. Phys. 68, 2959–2970 (1978)
Gilmanshin, R., Williams, S., Callender, R. H., Woodruff, W. H. & Dyer, R. B. Fast events in protein folding: relaxation dynamics of secondary and tertiary structure in native apomyoglobin. Proc. Natl Acad. Sci. USA 94, 3709–3713 (1997)
Ballew, R. M., Sabelko, J. & Gruebele, M. Direct observation of fast protein folding: the initial collapse of apomyoglobin. Proc. Natl Acad. Sci. USA 93, 5759–5764 (1996)
Plaxco, K. W., Simons, K. T. & Baker, D. Contact order transition state placement and the refolding rates of single domain proteins. J. Mol. Biol. 277, 985–994 (1998)
Moore, S. & Stein, W. Amino acid determination, methods and techniques. J. Biol. Chem. 192, 663–670 (1951)
Ponder, J. W. & Richards, F. M. An efficient Newton-like method for molecular mechanics energy minimization of large molecules. J. Comput. Chem. 8, 1016–1024 (1987)
Fletcher, R. & Powell, M. J. D. A rapidly convergent descent method for minimization. Comput. J. 6, 163–168 (1963)
Koehl, P. & Delarue, M. On the use of a self-consistent mean field theory to predict protein side chain conformations and estimate their entropies. J. Mol. Biol. 239, 249–275 (1994)
Qiu, D., Shenkin, P. S., Hollinger, F. P. & Still, W. C. The GB/SA Continuum model for solvation. A fast analytical method for the calculation of approximate Born radii. J. Phys. Chem. A 101, 3005–3014 (1997)
Jorgensen, W. L. & Tirado-Rives, J. The OPLS force field for proteins. Energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 110, 1657–1666 (1988)
Andersen, H. C. Rattle: a ‘velocity’ version of the shake algorithm for molecular dynamics calculations. J. Comput. Phys. 52, 24–34 (1983)
Kabsch, W. & Sander, C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers 22, 2577–2637 (1983)
Acknowledgements
We thank the Folding@Home volunteers whose processor power made this work possible; the members of the Pande, Levitt and Gruebele laboratories for discussion; J. Ottesen for the BBA5 coordinates; B. Imperiali for NMR data; the UIUC Laboratory for Fluorescence Dynamics; and the Suslick group for equipment use. C.S. was supported by a pre-doctoral Howard Hughes Medical Institute fellowship. V.P. and the Folding@Home project were supported by the National Institutes of Health (NIH), American Chemical Society-Petroleum Research Fund, National Science Foundation Materials Research Science & Engineering Centers, Center on Polymer Interfaces and Macromolecular Assemblies seed funds, and a gift from Intel. H.N. was supported by an NIH biophysics training grant. H.N. and M.G. were also funded by the NIH.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing financial interests.
Rights and permissions
About this article
Cite this article
Snow, C., Nguyen, H., Pande, V. et al. Absolute comparison of simulated and experimental protein-folding dynamics. Nature 420, 102–106 (2002). https://doi.org/10.1038/nature01160
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/nature01160
This article is cited by
-
Molecular dynamics simulations suggest the potential toxicity of fluorinated graphene to HP35 protein via unfolding the α-helix structure
Scientific Reports (2024)
-
Moderate binding of villin headpiece protein to C3N3 nanosheet reveals the suitable biocompatibility of this nanomaterial
Scientific Reports (2023)
-
A litmus test for classifying recognition mechanisms of transiently binding proteins
Nature Communications (2022)
-
Rotaxane rings promote oblique packing and extended lifetimes in DNA-templated molecular dye aggregates
Communications Chemistry (2021)
-
Sampling of the conformational landscape of small proteins with Monte Carlo methods
Scientific Reports (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.