Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Letter
  • Published:

Measurement of a confinement induced neutron phase

Nature volume 417, pages 630–632 (2002)Cite this article

Abstract

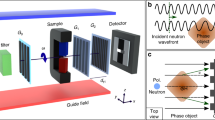
Particle physicists see neutrons as tiny massive particles with a confinement radius of about 0.7 fm and a distinct internal quark–gluon structure. In quantum mechanics, neutrons are described by wave packets whose spatial extent may become ten orders of magnitude larger than the confinement radius, and can even reach macroscopic dimensions, depending on the degree of monochromaticity. For neutrons passing through narrow slits, it has been predicted1,2 that quantization of the transverse momentum component changes the longitudinal momentum component, resulting in a phase shift that should be measurable using interferometric methods3. Here we use neutron interferometry to measure the phase shift arising from lateral confinement of a neutron beam passing through a narrow slit system. The phase shift arises mainly from neutrons whose classical trajectories do not touch the walls of the slits. In this respect, the non-locality of quantum physics is apparent.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on Springer Link
  • Instant access to full article PDF
Buy now

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Sketch of the slit structure and of the related neutron–wall interaction potential.
Figure 2: Expected phase shift as a function of the angle α of the incident beam component.
Figure 3: Sketch of the experimental set-up.
Figure 4: Typical interference pattern with and without the phase-shifting slit system (a) and the collection of the results of various scans (b).

Similar content being viewed by others

References

  1. Lévy-Leblond, J. M. A geometrical quantum phase effect. Phys. Lett. A 125, 441–442 (1987)

    Article  ADS  Google Scholar 

  2. Greenberger, D. M. A new non-local effect in quantum mechanics. Physica B 151, 374–377 (1988)

    Article  Google Scholar 

  3. Rauch, H. & Werner, S. A. Neutron Interferometry (Clarendon, Oxford, 2000)

    Google Scholar 

  4. Casimir, H. B. G. & Polder, D. Influence of retardation on the London-van der Waals forces. Phys. Rev. 73, 360–372 (1948)

    Article  ADS  CAS  Google Scholar 

  5. Haroche, S. & Raimond, J. M. Cavity quantum electrodynamics. Sci. Am. 268, 26–33 (1993)

    Article  Google Scholar 

  6. Fonda, L., Ghirardi, G. C., Rimini, A. & Weber, T. On the quantum foundations of the experimental decay law. Nuovo Cimento A 15, 689–704 (1973)

    Article  ADS  Google Scholar 

  7. Misra, B. & Sudarshan, E. C. G. The Zeno's paradox in quantum theory. J. Math. Phys. 18, 756–763 (1977)

    Article  ADS  MathSciNet  Google Scholar 

  8. Grisenti, R. E. et al. Determination of atom-surface van der Waals potentials from transmission diffraction intensities. Phys. Rev. Lett. 83, 1755–1758 (1999)

    Article  ADS  CAS  Google Scholar 

  9. Hegerfeldt, G. C. & Koehler, T. Deviations from classical optics in matter diffraction and determination of the size of weakly bound molecules. Phys. Rev. A 61, 023606-1–023606-10 (2000)

    Article  ADS  Google Scholar 

  10. Ferry, D. K., Grubin, H., Jacobini, C. & Jauho, A. J. (eds) Quantum Transport in Ultrasmall Devices (Plenum, New York, 1995)

  11. Salomon, C., Dalibard, J., Aspect, A., Metcalf, H. & Cohen-Tannoudji, C. Channeling atoms in a laser standing wave. Phys. Rev. Lett. 59, 1659–1662 (1987)

    Article  ADS  CAS  Google Scholar 

  12. Keller, C. et al. Adiabatic following in standing-wave diffraction of atoms. Appl. Phys. B 69, 303–309 (1999)

    Article  ADS  CAS  Google Scholar 

  13. Allman, B. E., Cimmino, A., Griffin, S. L. & Klein, A. G. Quantum phase shift caused by spatial confinement. Found. Phys. 29, 325–332 (1999)

    Article  Google Scholar 

  14. Nesvizhevsky, V. V. et al. Quantum states of neutrons in the Earth's gravitational field. Nature 415, 297–299 (2002)

    Article  ADS  Google Scholar 

  15. Flügge, S. Practical Quantum Mechanics (Springer, Berlin, 1971)

    MATH  Google Scholar 

  16. Pokotilovski & Yu, N. Quantum phase shift of spatially confined de Broglie waves in a gravitational field. Phys. Lett. A 248, 114–116 (1998)

    Article  ADS  CAS  Google Scholar 

  17. Rauch, H., Wölwitsch, H., Kaiser, H., Clothier, R. & Werner, S. A. Measurement and characterization of the three-dimensional coherence function in neutron interferometry. Phys. Rev. A 53, 902–908 (1996)

    Article  ADS  CAS  Google Scholar 

  18. Rauch, H. & Summhammer, J. Neutron interferometer absorption experiments in the quantum limit. Phys. Rev. A 46, 7284–7287 (1992)

    Article  ADS  CAS  Google Scholar 

Download references

Acknowledgements

This work was supported by the Austrian Science Foundation and a TMR-Network of the European Union EU. Useful discussions with J. Summhammer and D. Petrascheck are gratefully acknowledged.

Author information

Authors and Affiliations

  1. Atominstitut der Österreichischen Universitäten, Wien, A-1020, Austria

    H. Rauch, H. Lemmel, M. Baron & R. Loidl

  2. Institut Laue-Langevin, BP 156, Grenoble, F-38042, France

    M. Baron & R. Loidl

Authors
  1. H. Rauch
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. Lemmel
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Baron
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. R. Loidl
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to H. Rauch.

Ethics declarations

Competing interests

The authors declare that they have no competing financial interests.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rauch, H., Lemmel, H., Baron, M. et al. Measurement of a confinement induced neutron phase. Nature 417, 630–632 (2002). https://doi.org/10.1038/nature00773

Download citation

  • Received:

  • Accepted:

  • Issue Date:

  • DOI: https://doi.org/10.1038/nature00773

This article is cited by

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing