Introduction

Advances in microfluidic technology have caused the development of the Lab-on-a-Chip (LoC) concept. The LoC paradigm can be resumed in the will to emulate all the functionalities of a modern analysis laboratory onboard a portable platform, or at least a compact system, realizable at contained costs1. A LoC is extremely promising as a toolkit to embed diagnostics functions to be used at the point-of-care, allowing first screenings or accurate analysis of biological samples2, 3, 4 in the absence of adequate facilities, for example, in developing countries and low-resource settings5, 6, 7, 8. The spreading of LoC technology also opens it to significant exploitations for environmental monitoring and the emerging field of telemedicine6, 8.

An ideal LoC microscopy system should satisfy the following three main requirements: high-throughput data collection, label-free imaging and quantitative measurements. Many high-throughput imaging systems have been developed5, 7, 9, 10, 11, 12, 13. Label-free approaches are preferred to avoid sample pretreatment and to avoid altering the natural behavior of biological specimens. In addition, phase retrieval is highly demanded to yield quantitative information from the observed samples. In this framework, digital holography (DH) microscopy well matches the LoC requirements7, 10, 13, 14, 15, 16, and it has been successfully applied in tracking biological samples15, the study of cell mechanics17, and the study of cell life cycle and cell death18, 19, 20, with quantitative assessments19.

Much effort has been spent to exploit the flow of samples in a microfluidic environment to provide imaging with a reduced number of optical components embedded onboard a chip. In some cases, accurate microfluidic control was used to provide imaging with novel features and improved capabilities. The optofluidic microscope, introduced in 2006 by Heng et al21, represented a cutting-edge novelty in this direction, overcoming the resolution limits imposed by the finite size of the charged-coupled device (CCD) recording elements. However, phase retrieval was not allowed by such configuration, thus impairing the access to quantitative information.

The on-chip flow cytometry of leukocyte cells was demonstrated with the design of a compact in-line DH microscope using a pulsed, fiber-coupled laser source22. The light sheet microscope is a good example of exploiting the microfluidic environment for cytometry and imaging purposes23. In Refs. 10, 13 the two-dimensional (2D) recording device was replaced by a compact linear sensor array embedded onboard chip, and DH amplitude and phase-contrast reconstructions with unlimited field-of-view (FoV) were obtained. Recently, on-chip tomography exploiting the object flow was reported, where light diffracted from a slit illuminated the flowing samples with different incidence angles, and a cylindrical lens was used to collect the corresponding contributions24. Remarkably, refocusing capabilities and the recovery of differential phase contrast images was reported, although quantitative phase-contrast mapping was not achieved. Full-field imaging was also demonstrated by adopting a multi-wavelength strategy, where three laser diodes were used as monochromatic light sources, and an iterative phase-retrieval approach based on the Gerchberg-Saxton algorithm was followed25, 26. In the work conducted by Gorthi et al27, amplitude images of the sample were collected while it was allowed to flow along a tilted microfluidic channel. The microfluidic system acts as a flow cytometer, aligning cells and permitting analysis of one of them at a time. This simple configuration allowed for collecting a stack of intensities at different planes normal to the optical axis; thus, the phase retrieval was practicable by solving the transport of intensity equation (TIE)27, 28. However, this approach to the phase-retrieval problem requires solving the TIE under proper prior information regarding the boundary conditions28. Moreover, whenever multiple samples overlap inside the FoV, or the object size is larger than the FoV in one or both dimensions, the performance of TIE solvers dramatically worsen; thus, an efficient and robust solution to the TIE is still an issue9.

The use of light-emitting diodes (LEDs) for coherent imaging scopes is a relatively recent, though deeply investigated, topic29, 30. Based on lensless digital in-line holography (DILH), holographic optofluidic microscopy (HOM) was the first effort to develop compact devices equipped with holographic imaging modules and cheap LED sources30. Based on the same principle, on-chip tomography of model organisms was achieved by rotating the LED source31.

However, in any strategy based on DILH, proper iterative algorithms are used to solve the twin image problem. Since their convergence to a solution is not always guaranteed, HOM and TIE-based methods are discovered to be non-quantitative in a number of practical situations where cell alignment is unfeasible9, 25, 29, 32. Furthermore, the lensless approach constitutes an inner limitation to the available resolution, and proper algorithms need to be developed, mainly based on subpixel shifting, to push this beyond the limit imposed by the pixel size33. To get rid of the shortages originating from the twin image superposition, a spatial carrier should be introduced, thus resulting in the need to adopt an off-axis DH configuration.

In this work, instead of avoiding the use of lenses, we propose an alternative lens-based approach that integrates the imaging functions onboard chip. Our strategy is to move complexity from the reconstruction algorithms and the external imaging apparatus to the chip itself, using custom optical components for coherent imaging purposes. The concept of using a low-cost commercial chip and making it smarter by functionalizing it is a fascinating novelty. The latest advances in the field of photolithography and polymer printing offer a remarkable opportunity in this sense. Forward electrohydrodynamic (EHD) ink-jet printing, which can deliver polymer lenses forward any kind of surface without electrodes, nozzles, or constraints on the thickness of the receiving substrate, has recently been introduced34, 35, 36. Direct delivery on several devices is now allowed, opening new routes for the optical functionalization of cheap, commercial LoC platforms.

Here, we design, realize and test a microfluidic chip equipped with holographic imaging functionalities. It is conceived as a wavefront division interferometer allowing for off-axis DH recordings using only a single beam. Our scheme exploits optical components realized on a commercial chip to replace the macroscopic interferometers adopted in the common DH apparatus. The quasi-common path configuration enhances the stability of fringe patterns for a better portability. It is possible, then, to use this device as a compact DH microscope or to convert any conventional microscope into a holographic one, making a further step toward fully miniaturized and portable DH microscopy on chips.

Materials and methods

The microfluidic device

To integrate DH microscopy on a chip, an important goal is the simplification of the recording apparatus. To this end, our DH microscopy chip is conceived as a wavefront division interferometer allowing off-axis DH recordings.

Chip design

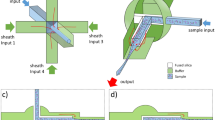
The commonly adopted DH apparatus is based on the interference between two beams following different paths and recombining in the acquisition plane. The scheme sketched in Figure 1a, however, is designed to produce off-axis holograms from single-beam illumination. This is realized by integrating a diffraction grating onto the chip bottom surface. The presence of the grating allows for the extraction of the reference wavefront directly from the object beam, thus enabling the formation of hologram fringes. Thereby, it is possible to use a single collimated beam to illuminate the chip provided that the diameter is large enough to impinge on both the channel and grating area. In this way, the beam is split into two parts: the object wavefront, which passes through the channel and encounters the flowing or static samples, and the reference beam, which is diffracted by the grating and interferes with the object wavefront at the image plane (see the right side of Figure 1a).

Figure 1
figure 1

Holographic module design. (a) Working principle of the single-beam interferometry. Bird’s-eye views of the parallel (b) and orthogonal (c) configurations.

Full size image

To explore the different possibilities our device offers, we implemented and tested two different configurations, with the grating oriented (i) parallel or (ii) orthogonal to the flow direction of the microfluidic channel, as respectively depicted in Figure 1b and 1c. The parallel configuration is designed to make it possible to have comparable imaging conditions all along the channel. This could be advantageous when multiple parallel measurements or scans along the entire length of the channel are required. The orthogonal grating design is preferable for applications that require the imaging of a fixed position of the channel. This is often the case in microfluidic devices, which exploit sample motion to collect information from all flowing objects. As we will show in the following, this configuration also makes it possible to double the FoV.

Grating design

When a plane wave normally impinges onto a sinusoidal one-dimensional transmission grating with period gP, it produces diffracted plane waves. These propagate on the other side at angles δi with the normal direction. Different exit angles correspond to the various diffraction orders emerging from the grating and are related to the grating period and the beam wavelength, λ, through the Equation (1):

As formerly explained, our strategy is to allow interference between the wavefront that passes through the sample and the first diffracting order from the grating.

To be effective, however, the angle should be tilted enough to produce well-sampled interference fringes that are not too far from the chip. Indeed, the choice of this angle determines the fringe spacing and, in turn, the separation of the diffraction orders in the Fourier domain. A proper separation allows for spatially filtering the orders of interest, which requires short fringe spacing. On the other hand, the fringe spacing must obey the Nyquist–Shannon sampling theorem, which poses a constraint on the maximum spatial carrier, as will be discussed in the following. Since the position of the diffraction orders also depends on the wavelength, this off-axis approach separates the contributions corresponding to different color channels, which can be spatially filtered in the Fourier domain. This would allow, in principle, simultaneous multi-wavelength recordings.

Digital holography

We will herein consider a wavefront division interferometric setup in the transmission microscopy configuration, as sketched in Figure 1a. Let O(ξ, η) and R(ξ, η) be the object beam and the reference beam, respectively, in the acquisition plane (ξ, η). The object wavefront, , passes through the sample, and its phase distribution, Ψ, carries information regarding the optical path delay (OPD) introduced on the impinging wavefront, which is related to the object optical thickness. The reference, R=aR exp{j2π(uRξ+vRη)}, is a plane wave oscillating with spatial frequencies uR and vR.

Due to the coherence of the light source, these two wavefronts are allowed to interfere in the plane (ξ, η) and to form a fringe pattern, that is, the hologram

where we omitted the dependence on the spatial coordinates (ξ, η) for the sake of clarity, ‘*’ indicates the conjugate operator, and we grouped the first two intensity terms in the signal H0, hereafter referred to as the zero-th order of diffraction. The last two terms on the right-hand side of Equation (2) contain the complex object; due to the off-axis angle introducing a spatial carrier, these can be separated in the Fourier domain. Indeed, since it results in H−1={H+1}*, we can rewrite Equation (2) in the form

where it is apparent that the amplitude and phase of the object wave are encoded as the amplitude and phase modulation, respectively, of a set of interference fringes equivalent to a carrier with spatial frequencies uR and vR. This gives us a good chance to recover the complex object via the demodulation of Equation (3).

The spatial frequencies are proportional to the angles between the reference and the object beam, (θξ, θη), according to the relation (uR, vR)=λ−1 (θξ, θη), which makes clear the advantage of using an off-axis configuration. If the object is acquired in its own best-focus plane, numerical propagation is not required and the information of interest is contained in the term H+1 Conversely, if an out-of-focus recording is performed, numerical propagation, Pz{…}, at the coordinate z yields the complex object in the reconstruction plane (x, y)

from which the amplitude image, |O (x, y)|, and the phase-contrast map, Ψ (x, y), can be extracted. In Equation (4), the operator Pz{…} performs the numerical propagation of the hologram, which is provided by solving the Fresnel–Kirchhoff diffraction integral, for example, by means of the Fresnel or the angular spectrum method37.

Results and discussion

Fabrication

The choice of the parameters for grating fabrication is related to the optimization of the optical setup constraints. First, the period of the interference fringes, Λ, should be short enough to ensure an efficient extraction of the reconstructed order in the Fourier space. On the other hand, the Nyquist criterion requires each fringe to be sampled by at least two pixels. However, a sampling rate of 3–4 pixels is usually the best compromise for practical purposes. In summary, given a CCD camera pixel size of 4.8 μm and a magnification of 10 ×, the optimal spacing falls between 0.96 and 1.92 μm for a sampling rate up to 4 pixels. These values correspond to the off-axis angles θ ranging from 19° to 38.5°, where θ=2arcsin(λ/2Λ) and λ=633 nm.

We fabricated the DH microscopy chip by inscribing a polymeric grating onboard a commercial microfluidic chip. The grating was inscribed by means of interference lithography38 on a positive photoresist (Microresist ma-P 1210), previously spun on the surface, with period gP=1.67 μm. With these settings, the reference beam, corresponding to the first diffraction order from the grating, forms an off-axis angle δ1=22.3°, which falls in the range of optimal sampling.

Digital holography on the chip

DH imaging was performed using a He-Ne laser with wavelength λ=633 nm (Melles-Griot). The collimated laser beam impinged the DH microscopy chip from the bottom side, that is, the grating side. The interference pattern generated by the chip was collected by a microscope objective (MO) (Zeiss 20 ×, NA=0,5) and imaged on a CCD camera (iDS uEye) through a Rayleigh lens system (f1=100, f2=50). The effective magnification on the camera was 10 ×.

We carried out the first experiments to test the DH microscopy chip on imaging diatoms of Thalassiosira rotula species and Caenorhabditis elegans (C. elegans) worms. C. elegans is often used as the model organism, playing a crucial role in the fundamental discovery, and may have high translational impact, presenting great advantages for feasibility and bioactivity testing in understanding biological diseases (see Supplementary Material for information regarding the samples and their preparation).

We acquired out-of-focus holograms for each class of objects while letting them flow inside the channel at arbitrary positions along the optical axis, corresponding to different focusing distances. Figure 2a and 2b shows two holograms acquired using the chip with parallel and orthogonal gratings, respectively. The formation of vertical fringes of interference is clearly appreciable in Figure 2a, modulated by the signal diffracted from diatoms forming chains. The off-axis spatial carrier has the effect of shifting the object distribution in the Fourier domain along the sole vR coordinate, as shown in the amplitude Fourier spectrum of Figure 2c. The chosen grating period is sufficient to separate the +1 order of interest, , denoted by a blue circle in Figure 2c, from the signal ; thus, this can be trivially extracted. The amplitude reconstruction, |H+1 (ξ, η)|, obtained after filtering the orders of interest out of the Fourier domain, is reported on the left side of Figure 2e, showing diatom chains that are slightly out of focus (the reconstruction parameter was set to z=0). After numerical propagation at z=3.57 cm, the diatom chain is refocused; see Figure 2e, right side. As expected, the refocused amplitude map of diatoms corresponds to an image with minimum contrast (diatoms are transparent at visible wavelengths), where these objects are barely visible. In this sense, the full-field feature of DH imaging is helpful because it gives access to the phase-contrast map of transparent samples, as will be shown in the following sections.

Figure 2
figure 2

(Media 1) Off-axis holography on chip. Holograms acquired with parallel (a) and orthogonal (b) gratings. A zoom of the interference fringes is shown in the insets. (c) and (d) Fourier spectra of the holograms in a and b, respectively. (e) Amplitude reconstruction and refocusing of diatoms from hologram a. (f) Amplitude reconstruction and refocusing of C. elegans in hologram b. Scale bar, 20 μm.

Full size image

Similarly, Figure 2b, 2d and 2f shows the entire process of reconstruction of a C. elegans worm, whose hologram is recorded using the configuration depicted in Figure 1c. The worm is recorded largely out of focus, as shown in Figure 2b, and horizontal fringes are visible with acceptable contrast, corresponding to a shift of the hologram spectrum mainly along the uR coordinate (see Figure 2d). The amplitude reconstruction before and after numerical refocusing is shown in Figure 2f on the left and right side, respectively. The refocused amplitude reconstruction in this case yields an image in which the object is well visible in its own best focus plane.

The process of fringe formation in the proposed scheme is shown in Media 1, where a z-scan of the MO is performed by progressively augmenting its distance from the chip, d, up to d=3 mm. At distances very close to the chip, the MO is not able to collect the interference between the object and the reference beam. Consequently, no hologram fringes are formed and the energy of the hologram spectrum is mainly distributed around the central spatial frequencies. When d augments, the MO gets closer to the interference plane depicted in Figure 1a, the horizontal fringes become visible, and the energy of the +1 order significantly increases because of the spatial carrier introducing the modulation described by Equation (3). Thus, off-axis DH is realized without the need for a separate arm of the interferometer.

Numerical refocusing

One of the most useful features of DH is the flexible focusing capability. This allows mapping in a 2D matrix the information of objects displaced at various heights inside a liquid volume, thus augmenting the throughput of a microfluidic system. Above all, an automatic search for the sample best focus plane is possible via optimization of a proper contrast metric39, that is, the Tamura coefficient . In the case of nearly transparent samples, this results in:

that is, the in-focus amplitude reconstruction minimizes TC (z). Conversely, at z=zfocus, the unwrapped phase-contrast map maximizes the contrast. The process of automatic refocusing of the hologram of Figure 2b is shown in Media 2 and Figure 3a, where the behavior of TC (z) vs z is plotted. Some significant amplitude reconstructions at different propagation distances are shown in the insets. As expected, the propagation distance minimizing the Tamura coefficient, z=15 cm, corresponds to the best-focus reconstruction of the object. Once this distance is estimated, the phase-contrast map of the worm can be extracted, which is shown in the inset denoted by a red box in Figure 3a.

Figure 3
figure 3

Automatic refocusing of the holographic reconstruction. (a) (Media 2) Behavior of Tamura index of the hologram of a C. elegans with propagation distance. The yellow-framed insets in a depict the amplitude reconstructions relative to the yellow circles. The red-framed insets depict amplitude and phase reconstruction at the estimated focal plane, denoted by a red circle. Scale bar, 50 μm. (b) (Media 3) Autofocusing of a hologram of T. rotula diatoms. Out-of-focus amplitude reconstructions are framed in yellow. In-focus amplitude and phase reconstructions are framed in red. Scale bar, 20 μm.

Full size image

Similarly, Figure 3b and Media 3 show the refocusing of diatom chains. In particular, a set of amplitude reconstructions is reported in Figure 3b, along with a sketch showing, for each of them, the corresponding values of TC (z). Again, the best-focus reconstruction provides a barely visible image of the diatoms (see the red box in the middle of Figure 3b) since these are pure phase objects. However, the phase distribution can be extracted from the complex wavefront corresponding to z=zfocus=2 cm. After phase unwrapping, the optical thickness distribution, Ψ (x, y), is retrieved in this plane, corresponding to an image with high contrast between the objects and the surrounding medium. This is shown in the red box on the right side of Figure 3b.

To better show that flexible focusing results in volumetric imaging, a further test is reported in Figure 4. Here, the hologram of several diatoms, recorded out of focus, is reconstructed at two different distances. This is a case where the objects occupy various positions inside the volume, corresponding to different refocusing distances. In a conventional optical microscope, a fixed acquisition plane should be selected to image the flowing objects in focus, thus loosing information regarding diatoms located in different planes. In contrast, a holographic z-scan solves this problem, refocusing all the flowing diatoms. Amplitude reconstructions are reported in Figure 4a and 4c, while the unwrapped phase-contrast maps corresponding to the yellow dashed boxes in Figure 4a and 4c is shown in Figure 4b and 4d. In Figure 4, the objects out of focus after DH propagation are indicated by a red circle, while the blue circle indicates the refocused objects. In particular, Figure 4a and 4b correspond to propagation at z=−1.53 cm, sufficient to put in focus the diatoms in the middle of the FoV. Finally, propagation at z=−3.57 cm provides refocusing of the diatom chain on the bottom-left corner, as reported in Figure 4c and 4d. The unwrapped phase contrast maps show the two chains clearly refocused at different planes. As expected, the object best-focus plane corresponds to the contrast maximization for the unwrapped phase distribution and a contrast minimization of the amplitude reconstruction.

Figure 4
figure 4

Holographic z-scan of flowing diatoms. Amplitude reconstructions numerically focused at z=−1.53 cm (a) and z=−3.57 cm (c) from the acquisition plane. Scale bar, 20 μm. The corresponding unwrapped phase-contrast maps of the region in the dashed frame are depicted in (b) and (d), respectively. Scale bar, 10 μm. Because of their transparency, in-focus diatoms (circled in blue) are barely visible in the amplitude images, while they maximize the phase signal. The opposite is true for out-of-focus diatoms (circled in red).

Full size image

Time-lapse coherent imaging

Unlike other imaging techniques, for example, scanning electron microscopy (SEM), transmission electron microscopy (TEM) or X-ray microscopy, DH does not require any sample preparation. Since no fluorophores are adopted, photobleaching issues are avoided. Hologram capture is a label-free, non-invasive recording modality, and numerical reconstruction can be performed in real time. Such features make DH especially suitable for working with live, moving samples without altering their natural behavior, and time-lapse imaging is allowed with a temporal resolution that is only limited by the features of the employed hardware.

First, we studied C. elegans worms in the early L2 stage. We let them move inside the channel, and we acquired time sequences of digital holograms using the holographic module described above. The frame rate of acquisition was set to 10 Hz. In Media 4, we report a sequence of recordings where one of the samples is acquired slightly out of focus. In particular, Media 4 shows both the recorded hologram and the sequence of modulus-2π phase-contrast maps obtained after demodulating Equation (3). Some significant frames extracted from Media 4 are reported in Figure 5a and 5b, in which the holograms and phase maps are respectively shown.

Figure 5
figure 5

Time-lapse imaging of moving, early L2 stage C. elegans. (Media 4) Holograms (a) and corresponding phase maps (b) of a worm moving inside a microfluidic channel acquired slightly out of focus. Scale bar, 50 μm. (Media 5) Phase maps of a moving sample acquired largely out of focus (c) and numerically refocused at z=15 cm (d). Scale bar, 50 μm. (Media 6) (e) Unwrapped phase-contrast images of a worm moving in the FoV. Scale bar, 20 μm.

Full size image

Media 5 and 6 show two sequences of holograms with C. elegans samples recorded largely out of focus. Therefore, once demodulated, numerical propagation is strictly demanded to recover reliable phase-contrast information. Figure 5c and 5d shows the modulus-2π phases of one of the two samples obtained before (z=0) and after refocusing (z=−15 cm), respectively (see also Media 5). Unwrapped phase contrast maps of a worm moving in the FoV are reported in Figure 5e, showing the worm optical thickness distribution and its changes due to the object motion. A sequence of 3D maps of the worm’s optical thickness is reported in Media 6. Finally, we studied a C. elegans worm in the adult stage by means of the compact imaging platform we proposed. Due to its developed inner structures, obtaining an optical thickness distribution of such sample is a challenging task. Nevertheless, here, we demonstrate the possibility of achieving this goal using the imaging module we introduced. In Figure 6a and 6b, the recorded holograms and the corresponding phase-contrast maps are, respectively, reported, showing the worm moving inside the FoV. In this case, due to its size, only portions of the sample are recognizable inside the FoV. However, phase maps were obtained with remarkable quality, in terms of signal-to-noise ratio, which allows for following the motion of the sample. Note that despite the low magnification factor we set, from the phase-contrast maps of Figure 6b, the worm body, its head and tail are visible with high contrast, allowing us to distinguish between different portions of this complex-shaped sample; some inner structures are detectable as well. In particular, in the image on the right side of Figure 6b, the worm uterus with embryos is clearly recognizable. This is also apparent from the phase-contrast profile plotted along a line crossing the embryos (see Figure 6c), which reports a measure of the absorption difference due to the passage of light through them.

Figure 6
figure 6

Time-lapse imaging of moving adult C. elegans. Recorded holograms (a) and corresponding phase-contrast maps (b) of an adult stage worm moving inside the FoV. Scale bar, 100 μm. Despite the low magnification, the phase-contrast maps allow for the distinction of different features of this complex-shaped sample; some inner structures are detectable as well. In particular, in the image on the right side of b, the worm uterus with embryos is clearly recognizable. This is also apparent from the phase-contrast profile plotted in c, which corresponds to the central line crossing the embryos in the yellow rectangle of b.

Full size image

Field-of-view extension

Here, we show the possibility to extend the FoV when using a chip in orthogonal configuration. In this configuration, in fact, both the object and reference beam pass through the microfluidic channel. This implies that a sample flowing in the channel will pass before in the area corresponding to the object beam, and after, in the area corresponding to the deflected reference beam. These two beams have slightly different optical paths. Hence, the sample is focused at different distances. Since these two zones are adjacent, one may think of it as an extended FoV whose information is stored on two different focal planes. Thanks to numerical refocusing, it is possible to recover the visual as well as the quantitative information of the sample at the focal distances relative to the two zones of the channel. The process of FoV retrieval is shown in Figure 7a, where the two cases are sketched. Depending on the position of the sample inside the channel, the undisturbed or the deflected wavefront can act as the object beam, and due to the difference in OPD, the object in the two different FoV can be recovered in focus by propagating the same hologram at two different z coordinates.

Figure 7
figure 7

(Media 7) Extended FoV configuration. (a) In this configuration, both interfering beams pass through the microfluidic channel. This way, as the sample (S) flows throughout the channel, it is illuminated by one beam or the other. Due to the different optical paths of the two beams (see a inset), the two images have different foci. This makes the two positions distinguishable and the information recoverable via numerical refocusing (see b–d). Scale bar, 20 μm.

Full size image

This is especially advantageous in the case of extended objects, when studying sample dynamics requires more imaging capabilities than simple cell counting. To make this point clearer, we first selected the hologram of a C. elegans worm lying across the two channel sections. Figure 7b shows the amplitude reconstruction of the hologram without propagation, where both halves of the worm body are largely out of focus. After applying the operator Pz{H+1} with z=z1=18.5 cm, one part of the worm is refocused, while the other half is still out of focus and barely visible (as shown in Figure 7c). Conversely, the second half of the object is clearly refocused by applying Pz{H+1} with z=z2=22 cm (see Figure 7d), thus demonstrating the recovery of both FoV. Media 7 shows the entire process of propagation that allows switching from one FoV to the other. It is apparent that the presence of an extended sample in both FoV is not critical to recover its signature; indeed, the entire object field can be obtained by sectioning and merging the reconstructions corresponding to Figure 7c and 7d. In the case of non-isolated objects, the issue of disturbing diffraction of out-of-focus samples in each of the FoVs can be treated as an unwanted background signal and can be filtered out using denoising techniques, as in classical DH.

As a further test, in Figure 8 and Media 8, we report the amplitude sequence of a worm swimming inside the channel and crossing the two FoV. In particular, Figure 8a and 8b shows the map of the worm after propagation at z1=−22.34 cm and z2=15.88 cm, respectively. The images showing the sample in focus are denoted by a red box. For each of them, the corresponding image in the yellow box shows the same object out of focus when this is seen through the other FoV.

Figure 8
figure 8

(Media 8) Time-lapse with extended FoV configuration. Amplitude images of an L1 stage C. elegans swimming in the microfluidic channel and passing from one FoV to the other. The same images are refocused at two different distances z1 (a) and z2 (b) corresponding to the two different FoV. The frames where the worm is in focus are marked in red. Scale bar, 50 μm.

Full size image

Remarkably, the accessibility of both FoV1 and FoV2, to follow the entire motion of the sample, is only possible thanks to the holographic recording and numerical flexible focusing, as shown in Media 8.

Pocket holographic slide

A further step toward the miniaturization of the holographic chip requires the replacement of the external MO with a proper embedded optical element.

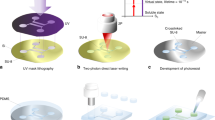
Lately, ink-jet printing technology has seen a wide range of applications within this scope. Among others, EHD-based techniques have shown promising results for printing with challenging spatial resolutions down to the nanoscale40. So far, EHD printing technologies have suffered from the same limitation, as the receiving substrate must be sandwiched between two electrodes at a well-defined distance. This geometrical requirement represents a severe constraint when materials must be directly dispensed onto devices ready for use.

Recently, forward pyro-EHD ink-jet printing has introduced the possibility to deliver, at nanoscale volume, drops forward the substrate without electrodes and a nozzle36. This removes the thickness constraint of the receiving substrate. Thus, printing directly onto several devices is now allowed, opening new possibilities in the field of optical functionalization of LoC devices. Here, we used forward pyro-EHD ink-jet printing to deliver polymer lenses to the chip surface to fully functionalize the commercial LoC and to obtain a holographic microscope slide.

A sketch of the setup is shown in Figure 9a, which illustrates the working principle. Pictures of a prototype apparatus with all the embedded optical components are shown in Figure 9b. On the chip, different portions are recognizable: a section with the polymeric diffraction grating (characterized by the reddish coloring of the photoresist); a clean section, which is the imaging window; and a set of microlenses layered along the channel.

Figure 9
figure 9

Pocket holographic module. The slide is conceived starting from the parallel configuration of the holographic chip. Here, the presence of a microlens in correspondence of the microfluidic channel provides the required magnification (a). (b) A prototype implementation of the module, comprising a CCD camera and the holographic chip with integrated microlenses. (Media 9) Time-lapse of a L1 stage C. elegans acquired using the prototype pocket holographic module (c). Scale bar, 100 μm. (Media 10) (d–e) Tracking of different worms swimming in the FoV at different heights. (f–g) 3D tracking plots of the worms in d and e, respectively.

Full size image

We tested our system using a polymer lens of 4.3 mm focal length and set the distance between the chip and camera to obtain a magnification M=15. DH amplitude imaging of a live C. elegans worm in the early embryonal stage is shown in Figure 9c and Media 9. The time sequence demonstrates the effectiveness of the pocket module with fully embedded optical components.

The DH flexible focusing capability can be exploited for three-dimensional (3D) tracking of a moving object inside a volume. The 3D tracking of various worms moving inside the FoV is shown in Figure 9d–9g and Media 10. The estimation of the center of mass of different objects on the image plane is also possible using non-holographic imaging techniques. Holographic imaging, however, permits the recovery of information of the third coordinate. This can be estimated by the propagation distance required to refocus the tracked object and automated by autofocusing algorithms. Figure 9d shows three frames of Media 10, in which three different worms are tracked. To estimate the worms’ center of mass, the same threshold is applied to all frames. The tracking on the image plane is performed while assuming a maximum displacement of 100 μm. The plot in Figure 9f shows the 3D trajectories of the worms in the observed volume. Similarly, Figure 9e and 9g, respectively show the 2D and 3D tracking of two worms moving closer to each other.

To increase the use of the pocket slide proposed for coherent microscopy, we introduced a further simplification in the microfabrication procedure. Once the system and its optical properties were tested, we adopted our prototype as a master for soft lithography. This process is used for shaping polymer materials using a microsized rigid frame, which in our case consists of the chip engineered via the printing of microlenses directly onto the channel and with the polymeric diffraction grating. The polymer we used is polydimethylsiloxane, chosen for its good optical and mechanical properties. A mold was cast from the object to be replicated. This mold was then filled with the prepolymer, which was cross-linked; the resulting polymer was peeled off the mold. The use of a mold rather than the object itself allows for the production of multiple copies without damaging the original. In this way, via replica molding, we produced flexible and transparent microengineered polymer layers that can be simply handled, put on top of the commercial channel of interest and peeled off once the imaging process is completed. The polymeric layer is portable and, because of its flexibility, could be easily adapted onto the device of interest.

Conclusions

In this work, we designed, implemented and tested a portable module that makes it possible to realize an off-axis DH microscope using a commercial LoC. Adopting a grating inscribed onto the chip surface, it is possible to efficiently extract a reference beam without an interferometer setup. Using polymer lenses printed on a chip, a single-beam DH microscope can be obtained, and the advantages of DH microscopy can be exploited without introducing setup complexity. In its complete version, the platform we proposed constitutes a pocket holographic microscope slide for LoC imaging. In the lack of polymer lenses delivered to the chip surface, a commercial chip can be used to convert an optical microscope into a holographic recording system.

Experiments shown in this manuscript demonstrate the effectiveness of the proposed scheme in capturing refocusable off-axis digital holograms with one single beam of coherent monochromatic light.

Unlike DILH and HOM, the introduced setup has no particular design constraints; thus, the distance between the light source and the chip can be minimized, which allows for reducing the size of the entire apparatus. Moreover, the spatial carrier allows for the direct extraction of the +1 diffraction order (containing the complex object information) by spatially filtering the hologram in the Fourier domain. Therefore, iterative algorithms and the related problems, mentioned above, can be avoided. High-quality phase contrast maps of complex-shaped objects were obtained. Remarkably, the configuration we proposed has been demonstrated to double the maximum achievable FoV.

The optical design introduced in this work could be particularly useful in the field of Point-of-Care diagnostics. Indeed, the single-beam interferometer scheme is very stable against vibrations of the optical system, sharing the advantages of all the common path interferometers that are suitable for on-field testing and industrial metrology applications41. In this sense, the robustness of the design we introduced allows this system to be brought out of the laboratory without requiring any vibration isolation system.

Future works will be devoted to the further minimization of the optical path difference between the object and reference beam. This is an essential requirement to replace bulky lasers with smaller and cheaper light sources and, therefore, for the realization of a compact on-chip DH microscope. Possible candidates could be solid state lasers. They combine good coherence properties with compactness, although the trade-off is lower cost effectiveness. An alternative could be to use cheaper diode lasers, which exhibit lower coherence but are smaller and lighter in weight. The ideal solution, however, would be replacing the coherent laser source with LEDs. Lately, various groups have proposed configurations to achieve off-axis DH microscopy using external optical components to address the low coherence of LEDs42, 43, 44, 45. Although effective, these do not fully exploit the advantage of using such a compact light source, as cumbersome interferometric schemes are required and a portable device has not been realized yet.

On the basis of these premises, we believe that adapting our scheme to the use of LED sources is worth of further investigation. Particular attention should be paid to the chip design to cope with the frequency dispersion introduced by the grating. Within this scope, the solution proposed in Ref. 42 could be a suitable starting point.