Abstract
Phase recovery from intensity-only measurements forms the heart of coherent imaging techniques and holography. In this study, we demonstrate that a neural network can learn to perform phase recovery and holographic image reconstruction after appropriate training. This deep learning-based approach provides an entirely new framework to conduct holographic imaging by rapidly eliminating twin-image and self-interference-related spatial artifacts. This neural network-based method is fast to compute and reconstructs phase and amplitude images of the objects using only one hologram, requiring fewer measurements in addition to being computationally faster. We validated this method by reconstructing the phase and amplitude images of various samples, including blood and Pap smears and tissue sections. These results highlight that challenging problems in imaging science can be overcome through machine learning, providing new avenues to design powerful computational imaging systems.
Similar content being viewed by others
Introduction
Optoelectronic sensor arrays, such as charge-coupled devices (CCDs) or complementary metal-oxide-semiconductor (CMOS)-based imagers, are only sensitive to the intensity of light; therefore, phase information of the objects or the diffracted light waves cannot be directly recorded using such imagers. Phase recovery from intensity-only measurements has emerged as an important field to recover this lost phase information in the detection process, enabling the reconstruction of the phase and amplitude images of specimen using various approaches1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13. In fact, Gabor’s original in-line holography system14, where the diffracted light from the object interferes with the background light that is directly transmitted, is an important example where phase recovery is required to separate the twin-image and self-interference-related spatial artifacts from the real image of the sample. In various implementations, to improve the performance of the phase recovery and image reconstruction processes, additional intensity information is recorded, for example, by scanning the illumination source aperture15, 16, 17, 18, sample-to-sensor distance19, 20, 21, 22, 23 (in some cases referred to as out-of-focus imaging24), wavelength of illumination25, 26, or phase front of the reference beam27, 28, 29, 30, among other methods31, 32, 33, 34, 35, 36. All these methods utilize additional physical constraints and intensity measurements to robustly retrieve the missing phase information based on an analytical and/or iterative solution that satisfies the wave equation. Some of these phase retrieval techniques have enabled discoveries in different fields37, 38, 39, 40.
In this paper, we report a convolutional neural network-based method, trained through deep learning41, 42, that can perform phase recovery and holographic image reconstruction using a single hologram intensity. Deep learning is a machine learning technique that uses a multi-layered artificial neural network for data modeling, analysis and decision making and has shown considerable success in areas where large amounts of data are available. Deep learning has recently been applied to solving inverse problems in imaging science such as in super-resolution43, 44, acceleration of the image acquisition speed of computed tomography (CT)45, magnetic resonance imaging (MRI)46, photoacoustic tomography47 and holography48, 49.
In this work, we used deep learning to rapidly perform phase recovery and reconstruct complex-valued images of specimen using a single intensity-only hologram. This process is very fast, requiring approximately 3.11 s on a graphics processing unit (GPU)-based laptop computer to recover the phase and amplitude images of a specimen over a field of view of 1 mm2 with ~7.3 megapixels in each image channel (amplitude and phase). We validated this approach by reconstructing the complex-valued images of various samples, such as blood and Papanicolaou (Pap) smears as well as thin sections of human tissue samples, all of which demonstrated successful elimination of the twin-image and self-interference-related spatial artifacts that arise due to lost phase information during the hologram detection process. In other words, the convolutional neural network, after its training, learned to extract and separate the spatial features of the real image from the features of the twin-image and other undesired interference terms for both the phase and amplitude channels of the object. Remarkably, this deep learning-based phase recovery and holographic image reconstruction approach has been achieved without any modeling of light–matter interaction or wave interference. However, this does not imply that the presented approach entirely ignores the physics of light–matter interaction and holographic imaging, which is in fact statistically inferred through deep learning in the convolutional neural network by using a large number of microscopic images as the gold standard in the training phase. This training and statistical optimization of the neural network is performed once and can be considered as part of a blind reconstruction framework that performs phase recovery and holographic image reconstruction using a single input such as an intensity-only hologram of the object. This framework introduces a myriad of opportunities to design fundamentally new coherent imaging systems and can be broadly applicable to any phase recovery problem, spanning different parts of the electromagnetic spectrum, including visible wavelengths as well as X-rays28, 30, 50, 51.
Results and discussion
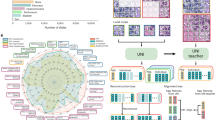
Our deep neural network approach for phase retrieval and holographic image reconstruction is schematically described in Figure 1 (see also Supplementary Figs. S1–S4). In this work, we chose to demonstrate the proposed framework using lens-free digital in-line holography of transmissive samples, including human tissue sections and blood and Pap smears (see Matrials and Methods). Due to the dense and connected nature of these samples that we imaged, their holographic in-line imaging requires the acquisition of multiple holograms for accurate and artifact-free object recovery52. A schematic of our experimental setup is shown in Supplementary Fig. S5, where the sample is positioned very close to a CMOS sensor chip with a <1 mm sample-to-sensor distance, which provides an important advantage in terms of the sample field of view that can be imaged. However, due to this relatively short sample-to-sensor distance, the twin-image artifact of the in-line holography, which is a result of the lost phase information, is strong and severely obstructs the spatial features of the sample in both the amplitude and phase channels, as illustrated in Figures 1 and 2.
Following its training phase, the deep neural network blindly outputs artifact-free phase and amplitude images of the object using only one hologram intensity. This deep neural network is composed of convolutional layers, residual blocks and upsampling blocks (see Supplementary Information for additional details) and rapidly processes a complex-valued input image in a parallel, multi-scale manner.
Comparison of the holographic reconstruction results for different types of samples: (a-h) Pap smear, (i-p) breast tissue section. (a, i) Zoomed-in regions of interest from the acquired holograms. (b, c, j, k) Amplitude and phase images resulting from free-space back-propagation of a single hologram intensity, shown in a and i, respectively. These images are contaminated with twin-image and self-interference-related spatial artifacts due to the missing phase information in the hologram detection process. (d, e, l, m) Corresponding amplitude and phase images of the same samples obtained by the deep neural network, demonstrating the blind recovery of the complex object image without twin-image and self-interference artifacts using a single hologram. (f, g, n, o) amplitude and phase images of the same samples reconstructed using multi-height phase retrieval with 8 holograms acquired at different sample-to-sensor distances. (h, p) corresponding bright-field microscopy images of the same samples, shown for comparison. The yellow arrows point to artifacts in f, g, n, o (due to out-of-focus dust particles or other unwanted objects) that are significantly suppressed by the network reconstruction, as shown in d, e, l, m.
The first step in our deep learning-based phase retrieval and holographic image reconstruction framework consists of ‘training’ the neural network. This training involves learning the statistical transformation between a complex-valued image that results from the back-propagation of a single intensity-only hologram of the object and the same object’s image that is reconstructed using a multi-height phase retrieval algorithm (treated as the gold standard for the training phase). This algorithm uses 8 hologram intensities acquired at different sample-to-sensor distances (see Materials and Methods as well as Supplementary Information). As illustrated in Figures 1,2,3, a simple back-propagation of the object’s hologram, without phase retrieval, contains severe twin-image and self-interference-related artifacts, hiding the phase and amplitude information of the object. This training/learning process (which is performed only once) results in a fixed deep neural network that is used to blindly reconstruct the phase and amplitude images of any object, free from twin-image and other undesired interference-related artifacts, using a single hologram intensity.
Red blood cell volume estimation using our deep neural network-based phase retrieval. The deep neural network output (e, f), given the input (c, d) obtained from a single hologram intensity (b), shows a good match with the multi-height phase recovery-based cell volume estimation results (a), calculated using Nholo=8 (g, h). Similar to the yellow arrows shown in Figure 2f, 2g, 2n and 2o, the multi-height phase recovery results exhibit an out-of-focus fringe artifact at the center of the field-of-view in (g, h). Refer to Supplementary Information for the calculation of the effective refractive volume of cells.
In our holographic imaging experiments, we used three different types of samples: blood smears, Pap smears and breast tissue sections, and separately trained three convolutional neural networks for each sample type, although the network architecture was identical in each case, as shown in Figure 1. To avoid over-fitting the neural network, we stopped the training when the deep neural network performance on the validation image set (which is different from the training image set and the blind testing image set) began to decline. We also accordingly made the network compact and applied pooling approaches53. Following this training process, each deep neural network was blindly tested with different objects that were not used in the training or validation image sets. Figures 1,2 and 3 show the neural network-based blind reconstruction results for the Pap smears, breast tissue sections and blood smears. These reconstructed phase and amplitude images clearly demonstrate the success of our deep neural network-based holographic image reconstruction approach to blindly infer artifact-free phase and amplitude images of the objects, matching the performance of the multi-height phase recovery. Table 1 further compares the structural similarity54 (SSIM) of our neural network output images (using a single input hologram, that is, Nholo=1) against the results obtained with a traditional multi-height phase retrieval algorithm using multiple holograms (that is, Nholo=2, 3,…,8) acquired at different sample-to-sensor distances. A comparison of the SSIM index values reported in Table 1 suggests that the imaging performance of the deep neural network using a single hologram is comparable to that of multi-height phase retrieval, closely matching the SSIM performance of Nholo=2 for both Pap smear and breast tissue samples and the SSIM performance of Nholo=3 for blood smear samples. The deep neural network-based reconstruction approach reduces the number of holograms required by 2-3 times. In addition to this reduction in the number of holograms, the computation time for holographic reconstruction using a neural network is also improved by more than three- and four-fold compared with those of the multi-height phase retrieval using Nholo=2 and Nholo=3, respectively (see Table 2).
The phase retrieval performance of our neural network is further demonstrated by imaging red blood cells (RBCs) in a whole blood smear. Using the reconstructed phase images of RBCs, the relative phase delay with respect to the background (where no cells are present) is calculated to reveal the phase integral per RBC (given in units of rad·μm2—see Supplementary Information for details), which is directly proportional to the volume of each cell, V. In Figure 3a, we compare the phase integral values of 127 RBCs in a given region of interest, which were calculated using the phase images of the network input, the network output, and the multi-height phase recovery image obtained with Nholo=8. Due to the twin-image and other self-interference-related spatial artifacts, the effective cell volume and the phase integral values calculated using the network input image demonstrated a highly random behavior. This behavior is shown as the scattered blue dots in Figure 3a and is significantly improved by the network output, shown as the red dots in the same figure.
Next, to evaluate the tolerance of the deep neural network and its holographic reconstruction framework to axial defocusing, we digitally back-propagated the hologram intensity of a breast tissue section to different depths, that is, defocusing distances within a range of z=[−20 μm, +20 μm] with Δz=1 μm increments. After this defocusing, we then fed each resulting complex-valued image as input into the same fixed neural network, which was trained by using in-focus images at z=0 μm. The amplitude SSIM index of each network output was evaluated with respect to the multi-height phase recovery image with Nholo=8 used as the reference (Figure 4). Although the deep neural network was trained with in-focus images, Figure 4 demonstrates the ability of the network to blindly reconstruct defocused holographic images with a negligible drop in image quality across the imaging system’s depth of field, which is ~4 μm.
Estimation of the depth defocusing tolerance of the deep neural network. (a) SSIM index for the neural network output images when the input image is defocused (that is, deviates from the optimal focus used in the training of the network). The SSIM index compares the network output images in d, f and h, with the image obtained by using the multi-height phase recovery algorithm with Nholo=8, shown in b.
In a digital in-line hologram, the intensity of the light incident on the sensor array can be written as

where A is the uniform reference wave that is directly transmitted and a(x,y) is the complex-valued light wave that is scattered by the sample. Under plane wave illumination, we can assume that A has zero phase at the detection plane, without loss of generality, that is, A=|A|. For a weakly scattering object, the self-interference term |a(x,y)|2 can be ignored compared with the other terms in Equation (1) because  . As detailed in our Supplementary Information, none of the samples that we imaged in this work satisfies this weakly scattering assumption. More specifically, the root-mean-squared (RMS) modulus of the scattered wave was measured to be approximately 28%, 34% and 37% of the reference wave RMS modulus for breast tissue, Pap smear and blood smear samples, respectively. This is why, for in-line holographic imaging of such strongly scattering and structurally dense samples, self-interference-related terms, in addition to twin-image terms, form strong image artifacts in both the phase and amplitude channels of the sample, making it difficult to apply object support-based constraints for phase retrieval. This necessitates additional holographic measurements for traditional phase recovery and holographic image reconstruction methods such as the multi-height phase recovery approach that we used for comparison in this work. Without increasing the number of holographic measurements, our deep neural network-based phase retrieval technique can learn to separate/clean the phase and amplitude images of the objects from twin-image and self-interference-related spatial artifacts, as illustrated in Figures 1, 2, 3. In principle, one could also use off-axis interferometry55, 56, 57 to image strongly scattering samples. However, this would create a penalty in the resolution or field of view of the reconstructed images due to the reduction in the space-bandwidth product of an off-axis imaging system.
. As detailed in our Supplementary Information, none of the samples that we imaged in this work satisfies this weakly scattering assumption. More specifically, the root-mean-squared (RMS) modulus of the scattered wave was measured to be approximately 28%, 34% and 37% of the reference wave RMS modulus for breast tissue, Pap smear and blood smear samples, respectively. This is why, for in-line holographic imaging of such strongly scattering and structurally dense samples, self-interference-related terms, in addition to twin-image terms, form strong image artifacts in both the phase and amplitude channels of the sample, making it difficult to apply object support-based constraints for phase retrieval. This necessitates additional holographic measurements for traditional phase recovery and holographic image reconstruction methods such as the multi-height phase recovery approach that we used for comparison in this work. Without increasing the number of holographic measurements, our deep neural network-based phase retrieval technique can learn to separate/clean the phase and amplitude images of the objects from twin-image and self-interference-related spatial artifacts, as illustrated in Figures 1, 2, 3. In principle, one could also use off-axis interferometry55, 56, 57 to image strongly scattering samples. However, this would create a penalty in the resolution or field of view of the reconstructed images due to the reduction in the space-bandwidth product of an off-axis imaging system.
Another important property of this deep neural network-based holographic reconstruction framework is that it significantly suppresses out-of-focus interference artifacts, which frequently appear in holographic images due to dust particles or other imperfections in various surfaces or optical components of the imaging setup. These naturally occurring artifacts are also highlighted in Figure 2f, 2g, 2n, 2o with yellow arrows and cleaned in the corresponding network output images of Figure 2d, 2e, 2l, 2m. From the perspective of our trained neural network, this property to suppress out-of-focus interference artifacts stems from the fact that these holographic artifacts fall into the same category as twin-image artifacts due to the spatial defocusing operation, helping the trained network reject such artifacts in the reconstruction process. This is especially important for coherent imaging systems because various unwanted particles and features form holographic fringes on the sensor plane and superimpose on the object’s hologram, degrading the perceived image quality after image reconstruction.
In this study, we used the same neural network architecture depicted in Figure 1 and Supplementary Figs. S1–S2 for all object types, and based on this design, we separately trained the convolutional neural network for different types of objects (for example, breast tissue vs Pap smear). The neural network was then fixed after the training process to blindly reconstruct the phase and amplitude images of any object of the same type. If a different type of sample (for example, a blood smear image) was used as an input for a specific network trained on a different sample type (for example, Pap smear images), reconstruction artifacts would appear, as exemplified in Supplementary Fig. S6. However, this does not pose a limitation because in most imaging experiments, the type of the sample is known, although its microscopic features are unknown and must be revealed with a microscope. This is the case for biomedical imaging and pathology since the samples are prepared (for example, stained and fixed) with the correct procedures, tailored for the type of the sample. Therefore, the use of an appropriately trained neural network for a given type of sample can be considered well aligned with traditional uses of digital microscopy tools.
We also created and tested a universal neural network that can reconstruct different types of objects after its training, based on the same architecture used in our earlier networks. To handle different object types using a single neural network, we increased the number of feature maps in each convolutional layer from 16 to 32 (Supplementary Information), which also increased the complexity of the network, leading to increased training times. However, the reconstruction runtime (after the network was fixed) increased marginally from approximately 6.45 s to 7.85 s for a field of view of 1 mm2 (Table 2). Table 1 also compares the SSIM index values achieved using this universal network, which performed similarly to the individual object-type-specific networks. A further comparison between the holographic image reconstructions achieved by this universal network and the object-type-specific networks is also provided in Figure 5, confirming the same conclusion as in Table 1.
Comparison of the holographic image reconstruction results for the sample-type-specific and universal deep networks for different types of samples. The deep neural network used a single hologram intensity as input, whereas Nholo=8 was used in the column on the right. (a–f) Blood smear. (g–l) Papanicolaou smear. (m–r) Breast tissue section.
Conclusions
In this paper, we demonstrated that a convolutional neural network can perform phase recovery and holographic image reconstruction after training. This deep learning-based technique provides a new framework in holographic image reconstruction by rapidly eliminating twin-image and self-interference-related artifacts using only one hologram intensity. Compared to existing holographic phase recovery approaches, this neural network framework is significantly faster to compute and reconstructs improved phase and amplitude images of the objects with less number of measurements.
Materials and methods
Multi-height phase recovery
To generate the ground truth amplitude and phase images used to train the neural network, phase retrieval was achieved by using a multi-height phase recovery method19, 21, 22. For this purpose, the image sensor is shifted in the z direction away from the sample by ~15 μm increments 6 times and ~90 μm increment once, resulting in 8 different relative z positions of approximately 0, 15, 30, 45, 60, 75, 90 and 180 μm. We refer to these positions as the 1st, 2nd, …, 8th heights, respectively. The holograms at the 1st, 7th and 8th heights are used to initially calculate the optical phase at the 7th height, using the transport of intensity equation (TIE) through an elliptic equation solver52 implemented in MATLAB (Release R2016b, The MathWorks, Inc., Natick, MA, USA). Combined with the square root of the hologram intensity acquired at the 7th height, the resulting complex field is used as an initial guess for the subsequent iterations of the multi-height phase recovery. This initial guess is digitally refocused to the 8th height, where the amplitude of the guess is averaged with the square root of the hologram intensity acquired at the 8th height, and the phase information is kept unchanged. This updating procedure is repeated at the 7th, 6th,..., 1st heights, which defines one iteration of the algorithm. Usually, 10–20 iterations give satisfactory reconstruction results. However, to ensure the optimality of the phase retrieval for the training of the network, the algorithm is iterated 50 times, after which the complex field is back-propagated to the sample plane, yielding the amplitude and phase or real and imaginary images of the sample. These resulting complex-valued images are used to train the network and provide comparison images for the blind testing of the network output.
Generation of training data
To generate the training data for the deep neural network, each resulting complex-valued object image from the multi-height phase recovery algorithm, as well as the corresponding single hologram back-propagation image (which includes the twin-image and self-interference-related spatial artifacts), is divided into 5 × 5 sub-tiles with an overlap of 400 pixels in each dimension. For each sample type, this results in a dataset of 150 image pairs (that is, complex-valued input images for the network and the corresponding multi-height reconstruction images), which are divided into 100 image pairs for training, 25 image pairs for validation, and 25 image pairs for blind testing. The average computation time for the training of each sample-type-specific deep neural network (which is done only once) was ~14.5 h, whereas it increased to approximately 22 h for the universal deep neural network (refer to Supplementary Information for additional details). As an example, the progression of the universal network training as a function of the number of epochs is shown in Supplementary Fig. S4.
Speeding up holographic image reconstruction using GPU programming
As further detailed in the Supplementary Information, the pixel super-resolution and multi-height phase retrieval algorithms are implemented in C/C++ and accelerated using the CUDA Application Program Interface (API). These algorithms are run on a laptop computer using a single NVIDIA (Santa Clara, California) GTX 1080 graphics card. The basic image operations are implemented using customized kernel functions and are tuned to optimize the GPU memory access based on the access patterns of individual operations. GPU-accelerated libraries, such as cuFFT58 and Thrust59, are utilized for development productivity and optimized performance. The TIE initial guess is generated using a MATLAB-based implementation, which is interfaced using the MATLAB C++ engine API, allowing the overall algorithm to be maintained within a single executable after compilation.
Sample preparation
Breast tissue slide
Formalin-fixed paraffin-embedded (FFPE) breast tissue is sectioned into 2 μm slices and stained using hematoxylin and eosin (H&E). The de-identified and existing slides are obtained from the Translational Pathology Core Laboratory at UCLA.
Pap smear
De-identified and existing Papanicolaou smear slides were obtained from the UCLA Department of Pathology.
Blood smear
De-identified blood smear slides are purchased from Carolina Biological (Item # 313158).
References
Gerchberg RW, Saxton WO . A practical algorithm for the determination of phase from image and diffraction plane pictures. Optik 1972; 35: 237.
Fienup JR . Reconstruction of an object from the modulus of its Fourier transform. Opt Lett 1978; 3: 27–29.
Zalevsky Z, Mendlovic D, Dorsch RG . Gerchberg–Saxton algorithm applied in the fractional Fourier or the Fresnel domain. Opt Lett 1996; 21: 842–844.
Elser V . Solution of the crystallographic phase problem by iterated projections. Acta Crystallogr A 2003; 59: 201–209.
Luke DR . Relaxed averaged alternating reflections for diffraction imaging. Inverse Probl 2005; 21: 37–50.
Latychevskaia T, Fink HW . Solution to the twin image problem in holography. Phys Rev Lett 2007; 98: 233901.
Marchesini S . Invited Article: a unified evaluation of iterative projection algorithms for phase retrieval. Rev Sci Instrum 2007; 78: 011301.
Quiney HM, Williams GJ, Nugent KA . Non-iterative solution of the phase retrieval problem using a single diffraction measurement. Opt Express 2008; 16: 6896–6903.
Brady DJ, Choi K, Marks DL, Horisaki R, Lim S . Compressive holography. Opt Express 2009; 17: 13040–13049.
Szameit A, Shechtman Y, Osherovich E, Bullkich E, Sidorenko P et al. Sparsity-based single-shot subwavelength coherent diffractive imaging. Nat Mater 2012; 11: 455–459.
Candès EJ, Eldar YC, Strohmer T, Voroninski V . Phase retrieval via matrix completion. SIAM J Imaging Sci 2013; 6: 199–225.
Rodriguez JA, Xu R, Chen CC, Zou YF, Miao JW . Oversampling smoothness: an effective algorithm for phase retrieval of noisy diffraction intensities. J Appl Crystallogr 2013; 46: 312–318.
Rivenson Y, Aviv (Shalev) M, Weiss A, Panet H, Zalevsky Z . Digital resampling diversity sparsity constrained-wavefield reconstruction using single-magnitude image. Opt Lett 2015; 40: 1842–1845.
Gabor D . A new microscopic principle. Nature 1948; 161: 777–778.
Faulkner HML, Rodenburg JM . Movable aperture lensless transmission microscopy: a novel phase retrieval algorithm. Phys Rev Lett 2004; 93: 023903.
Dierolf M, Menzel A, Thibault P, Schneider P, Kewish CM et al. Ptychographic X-ray computed tomography at the nanoscale. Nature 2010; 467: 436–439.
Zheng GA, Horstmeyer R, Yang C . Wide-field, high-resolution Fourier ptychographic microscopy. Nat Photonics 2013; 7: 739–745.
Tian L, Waller L . 3D intensity and phase imaging from light field measurements in an LED array microscope. Optica 2015; 2: 104–111.
Misell DL . An examination of an iterative method for the solution of the phase problem in optics and electron optics: I. Test calculations. J Phys D Appl Phys 1973; 6: 2200–2216.
Teague MR . Deterministic phase retrieval: a Green’s function solution. J Opt Soc Am 1983; 73: 1434–1441.
Paganin D, Barty A, McMahon PJ, Nugent KA . Quantitative phase-amplitude microscopy. III. The effects of noise. J Microsc 2004; 214: 51–61.
Greenbaum A, Ozcan A . Maskless imaging of dense samples using pixel super-resolution based multi-height lensfree on-chip microscopy. Opt Express 2012; 20: 3129–3143.
Rivenson Y, Wu Y, Wang H, Zhang Y, Feizi A et al. Sparsity-based multi-height phase recovery in holographic microscopy. Sci Rep 2016; 6: 37862.
Wang H, Göröcs Z, Luo W, Zhang Y, Rivenson Y et al. Computational out-of-focus imaging increases the space–bandwidth product in lensbased coherent microscopy. Optica 2016; 3: 1422–1429.
Ferraro P, Miccio L, Grilli S, Paturzo M, De Nicola S et al. Quantitative Phase Microscopy of microstructures with extended measurement range and correction of chromatic aberrations by multiwavelength digital holography. Opt Express 2007; 15: 14591–14600.
Luo W, Zhang YB, Feizi A, Göröcs Z, Ozcan A . Pixel super-resolution using wavelength scanning. Light Sci Appl 2016; 5: e16060 doi:10.1038/lsa.2016.60.
Gonsalves RA . Phase retrieval and diversity in adaptive optics. Opt Eng 1982; 21: 215829.
Eisebitt S, Lüning J, Schlotter WF, Lörgen M, Hellwig O et al. Lensless imaging of magnetic nanostructures by X-ray spectro-holography. Nature 2004; 432: 885–888.
Rosen J, Brooker G . Non-scanning motionless fluorescence three-dimensional holographic microscopy. Nat Photonics 2008; 2: 190–195.
Marchesini S, Boutet S, Sakdinawat AE, Bogan MJ, Bajt S et al. Massively parallel X-ray holography. Nat Photonics 2008; 2: 560–563.
Popescu G, Ikeda T, Dasari RR, Feld MS . Diffraction phase microscopy for quantifying cell structure and dynamics. Opt Lett 2006; 31: 775–777.
Coppola G, Di Caprio G, Gioffré M, Puglisi R, Balduzzi D et al. Digital self-referencing quantitative phase microscopy by wavefront folding in holographic image reconstruction. Opt Lett 2010; 35: 3390–3392.
Wang Z, Millet L, Mir M, Ding HF, Unarunotai S et al. Spatial light interference microscopy (SLIM). Opt Express 2011; 19: 1016–1026.
Rivenson Y, Katz B, Kelner R, Rosen J . Single channel in-line multimodal digital holography. Opt Lett 2013; 38: 4719–4722.
Shechtman Y, Eldar YC, Cohen O, Chapman HN, Miao JW et al. Phase retrieval with application to optical imaging: a contemporary overview. IEEE Signal Process Mag 2015; 32: 87–109.
Kelner R, Rosen J . Methods of single-channel digital holography for three-dimensional imaging. IEEE Trans Ind Inform 2016; 12: 220–230.
Zuo JM, Vartanyants I, Gao M, Zhang R, Nagahara LA . Atomic resolution imaging of a carbon nanotube from diffraction intensities. Science 2003; 300: 1419–1421.
Song CY, Jiang HD, Mancuso A, Amirbekian B, Peng L et al. Quantitative imaging of single, unstained viruses with coherent X rays. Phys Rev Lett 2008; 101: 158101.
Miao JW, Ishikawa T, Shen Q, Earnest T . Extending X-ray crystallography to allow the imaging of noncrystalline materials, cells, and single protein complexes. Annu Rev Phys Chem 2008; 59: 387–410.
Loh ND, Hampton CY, Martin AV, Starodub D, Sierra RG et al. Fractal morphology, imaging and mass spectrometry of single aerosol particles in flight. Nature 2012; 486: 513–517.
LeCun Y, Bengio Y, Hinton G . Deep learning. Nature 2015; 521: 436–444.
Schmidhuber J . Deep learning in neural networks: An overview. Neural Netw 2015; 61: 85–117.
Dong C, Loy CC, He KM, Tang XO . Image super-resolution using deep convolutional networks. IEEE Trans Pattern Anal Mach Intell 2016; 38: 295–307.
Rivenson Y, Gorocs Z, Gunaydin H, Zhang YB, Wang HD et al Deep learning microscopy. Optica 2017; 4: 1437–1443.
Jin KH, McCann MT, Froustey E, Unser M . Deep convolutional neural network for inverse problems in imaging. IEEE Trans Image Process 2017; 26: 4509–4522.
Wang SS, Su ZH, Ying L, Peng X, Zhu S et al. Accelerating magnetic resonance imaging via deep learning. Proceedings of the 13th International Symposium on Biomedical Imaging (ISBI); 13-16 April 2016; Prague, Czech Republic. IEEE: Prague, Czech Republic 2016 doi:10.1109/ISBI.2016.7493320.
Antholzer S, Haltmeier M, Schwab J . Deep learning for photoacoustic tomography from sparse data. arXiv:1704.04587, 2017.
Jo Y, Park S, Jung J, Yoon J, Joo H et al. Holographic deep learning for rapid optical screening of anthrax spores. Sci Adv 2017; 3: e1700606.
Sinha A, Lee J, Li S, Barbastathis G . Lensless computational imaging through deep learning. arXiv: 1702.08516, 2017.
Bartels M, Krenkel M, Haber J, Wilke RN, Salditt T . X-ray holographic imaging of hydrated biological cells in solution. Phys Rev Lett 2015; 114: 048103.
McNulty I, Kirz J, Jacobsen C, Anderson EH, Howells MR et al. High-resolution imaging by Fourier transform X-ray holography. Science 1992; 256: 1009–1012.
Greenbaum A, Zhang YB, Feizi A, Chung PL, Luo W et al. Wide-field computational imaging of pathology slides using lens-free on-chip microscopy. Sci Transl Med 2014; 6: 267ra175–267ra175.
Nowlan SJ, Hinton GE . Simplifying neural networks by soft weight-sharing. Neural Comput 1992; 4: 473–493.
Wang Z, Bovik AC, Sheikh HR, Simoncelli EP . Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 2004; 13: 600–612.
Lohmann A . Optische einseitenbandübertragung angewandt auf das Gabor-Mikroskop. Opt Acta 1956; 3: 97–99.
Leith EN, Upatnieks J . Reconstructed wavefronts and communication theory. J Opt Soc Am 1962; 52: 1123–1130.
Goodman JW . Introduction to Fourier Optics. 3rd edn.Roberts and Company Publishers: Greenwood Village, Colorado; 2005.
cuFFT. NVIDIA Developer 2012. Available at https://developer.nvidia.com/cufft (accessed on 9th April 2017) (The content in the link is not NVIDIA Developer).
Thrust-Parallel Algorithms Library. Available at https://thrust.github.io/ (accessed and 9th April 2017) (The content in the link is not NVIDIA Developer).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Note: Supplementary Information for this article can be found on the Light: Science & Applications’ website.
Supplementary information
Rights and permissions
This work is licensed under a Creative Commons Attribution 4.0 Unported License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/
About this article
Cite this article
Rivenson, Y., Zhang, Y., Günaydın, H. et al. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light Sci Appl 7, 17141 (2018). https://doi.org/10.1038/lsa.2017.141
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1038/lsa.2017.141
Keywords
This article is cited by
-
On the use of deep learning for phase recovery
Light: Science & Applications (2024)
-
Ultrafast Bragg coherent diffraction imaging of epitaxial thin films using deep complex-valued neural networks
npj Computational Materials (2024)
-
The CellPhe toolkit for cell phenotyping using time-lapse imaging and pattern recognition
Nature Communications (2023)
-
Rapid and stain-free quantification of viral plaque via lens-free holography and deep learning
Nature Biomedical Engineering (2023)
-
Compressive holographic sensing simplifies quantitative phase imaging
Light: Science & Applications (2023)